Контрольные вопросы к разделу 6

16. Изобразите векторную модель колебания, модулированного по амплитуде суммой двух колебаний разных частот.

17. Постройте векторную модель ЧМ колебания при очень малом индексе частотной модуляции.

18. Катушка индуктивности и конденсатор соединены последовательно. Как отличаются векторы токов через эти элементы схемы?

19. Балансно-модулированное колебание образуется в результате перемножения модулирующей функции и несущего колебания. Постройте векторную модель такого колебания при гармонической модулирующей функции.

7. Спектральные модели сигналов.

7.1. Представление сигналов рядами Фурье

Сигналы часто описываются периодическими функциями, определенными на всей оси времени. Разумеется, такие сигналы физически нереализуемы: они имели бы бесконечную энергию. Но при всей ограниченности такой модели она давно и традиционно используется для представления сигналов не только в системах РЭБ, но и вообще в информационных системах различного функционального назначения и структуры, использующих не одиночные сигналы, а их упорядоченные последовательности. Очень часто такие последовательности на достаточно протяженных интервалах времени можно рассматривать как периодические последовательности импульсов или пачек импульсов. И для них справедливы условия, позволяющие применить разложения в ряды Фурье.

Еще в 1807 г. Фурье высказал предположение, что любая произвольная периодическая функция, даже та, которая имеет конечное число разрывов первого рода, может быть представлена бесконечным рядом вида

.

При этом уже до Фурье математики (Л. Эйлер, Д. Бернулли и др.) знали, что если колебание s(t) выражается рядом , то значения весовых коэффициентов a_n и b_n при суммируемых гармониках можно найти по формулам

,,.

Такой результат является следствием известного свойства ортогональности синусоид и косинусоид, частоты которых кратны некоторой основной частоте , обратной периоду повторения сигнала. Ряд на временном интервале длиныT складываются синусоиды и косинусоиды с частотами, образующими арифметическую прогрессию с разностью 1/T: . На интервалеT условия ортогональности тригонометрических функций, базисных для преобразования Фурье, выполнены, поскольку

При выполнении условий автоматически выполняется равенство, а значит,s(t) должна быть периодической функцией с периодом T.

В результате очевидной подстановки

ряд может быть представлен в форме

,

а используя комплексную форму модель представления гармонических колебаний, по которым разлагается сигнал, в форме

.

Комплексная амплитуда связана с амплитудойА_n и фазой j_n, а также с амплитудами гармонических составляющих ряда соотношениями

Амплитуды и– взаимно сопряженные комплексные величины

.

На основании можно также записать, что

,

Периодический сигнал при целом числеm®¥ и , так же, как и гармоническое колебаниепри, относится к простейшим моделям детерминированных сигналов. Поскольку значения периодического сигнала повторяются с периодомT бесконечное число раз, этот сигнал обладает бесконечно большой энергией, а значит, как и гармоническое колебание, является математической абстракцией, не соответствующей никакому реальному физическому процессу.

Очевидно, что из-за конечной продолжительности любых реальных процессов, рабочие сигналы РЭС принципиально не могут быть строго периодическими. Даже в тех случаях, когда говорят о периодических импульсных последовательностях зондирующих сигналов РЛС, сигналов радионавигационных систем и т.п., речь идет только об условно периодических сигналах. У реальных сигналов любой физической природы периодичность наблюдается всегда на некотором конечном отрезке времени, пространства, частотной оси. Поэтому лишь на отрезках времени, пространства и в полосе частот своего существования они действительно описываются соответствующими периодическими функциями времени, пространства, частоты. Вне этих отрезков и полосы такие функции описывают некоторые абстрактные процессы, не существующие в природе. Общепринятое название периодических на конечных отрезках сигналов – квазипериодические сигналы. К ним, как ко всякому конечному сигналу, применим интеграл Фурье. В случаях необходимости использования ряда Фурье правомерен вопрос о допустимости представления условно периодических (квазипериодических) сигналов рядом Фурье и, возможно, об условиях и точности такого представления.

По этому поводу высказываются следующие соображения. Аппроксимация рядом Фурье произвольного сигнала s(t), заданного на конечном отрезке , обеспечивается только на этом отрезке. Вне указанного отрезка ряд может сходиться кs(t), например, в смысле среднего квадрата ошибки, который не стремится к нулю. Если же s(t) периодическая функция с периодом T_п на оси -¥<t<¥, т.е.,n=1,2,3,…, то представляющий ее ряд Фурье сходится к s(t) в среднем квадратичном на каждом произвольно выбранном периодически повторяющемся отрезке , гдеt₀ – любая из точек оси t. В связи с этим, для представления квазипериодического сигнала s(t) рядом Фурье, надо считать его периодически продолженным на всей оси t и при таком предположении сформировать соответствующий ряд . Коэффициенты ряда следует находить только с учетом значений сигнала на временном интервале его реального существования.

Совокупность коэффициентов тригонометрического ряда принято изображать графически в координатах амплитуда-частота, как на рис. 7.1. Такую диаграмму называют частотным спектром сигнала, или просто спектром.

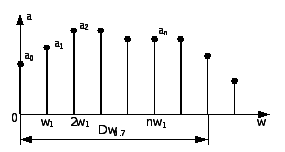
Рис.7.1. Спектр периодического сигнала

Аналогичным образом определяется распределение по частотам фаз гармонических составляющих спектра.

Часто для характеристики спектральных свойств сигнала пользуются не всей диаграммой, характеризующей распределение амплитуд по частотам гармонических составляющих, а более простыми величинами. Так показателем ширины спектра, называя ей диапазон частот, в пределах которого амплитуды гармонических составляющих не превышают некоторого заранее оговоренного уровня. На рис. 7.1. в ширина спектра сигнала определяется по уровню от максимума.