7.1.2. Частотные спектры непериодических сигналов

Физически реализуемый сигнал обязательно должен иметь конечную энергию. Если мощность сигнала отлична от нуля, то такой сигнал энергией должен быть ограничен во времени. Формально это условие равносильно требованию сходимости интеграла

,

где s²(t) – мгновенная мощность сигнала.

Для определения спектра такого сигнала он (сигнал), действующий на конечном интервале времени tÎ[t_н,t_к] рис. 7.6, доопределяется до периодического путем повторения s(t) с периодом T=t_к–t_н.

Рис. 7.6. Сигнал конечной длительности и последовательность его периодического повторения

Тогда для сигнала, превращенного в периодическую функцию, применимо разложение в ряд Фурье, причем коэффициенты этого ряда будут тем меньше, чем больше интервал Т, выбранный в качестве периода. Устремляя Т к бесконечности, в пределе можно получить бесконечно малые амплитуды гармонических составляющих, сумма которых приближается к исходной непериодической функции s(t), заданную в интервале tÎ[t_н,t_к]. Количество гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при Т®¥ основная частота функции . Иными словами, частотный интервал спектральными линиями, равный основной частотеw₁ становится бесконечно малым, а спектр – сплошным.

Итак, непериодическая функция имеет сплошной спектр, состоящий из бесконечно большого количества гармоник с бесконечно малыми амплитудами. Формально это выражается следующим образом

Использование этого соотношения в приводит к

Здесь учтено, что . При получается исходная непериодическая функцияs(t), заданная в интервале tÎ[t_н,t_к]. Очевидно, что при Т®¥ частота w₁ превращается в dw, nw₁ – в текущую частоту wQ, а операция суммирования – в операцию интегрирования. С учетом сказанного превращается в

.

Внутренний интеграл, являющийся функцией w

называется спектральной плотностью сигнала функции s(t).

В общем виде, когда не уточнены пределы t_н и t_в, спектральная плотность может быть представлена в форме

.

После подстановки в получается

.

Выражения и называются соответственно прямым и обратным преобразованиями Фурье. Из хода предыдущих рассуждений следует, что эти соотношения безусловно справедливы только для абсолютно интегрируемой функции s(t).

Сигнал s(t) в представляет собой непериодическую функцию в виде суммы (интеграла) гармонических колебаний с бесконечно малыми амплитудами. Сравнивая выражения и можно установить, что амплитуды этих составляющих равны и выяснить содержательный смысл термина "спектральная плотность". Выделив какую-либо дискретную частоту, соответствующую в случае периодической функцииn-ной гармонике, можно получить для амплитуды этой гармоники выражение

;

в случае же непериодической функции, совпадающей с s(t) в интервале tÎ[t_н,t_к], для спектральной плотности, соответствующей той же частоте w=w_n, получается следующее выражение:

.

Так как интегралы в правых частях этих выражений полностью совпадают, совпадают и левые, т.е.

или, учитывая что ,

Множитель 2 в знаменателе в правой части этого выражения учитывает, что при использовании комплексной формы ряда Фурье, в которой фигурируют отрицательные частоты, амплитуды гармоник равны .

Итак, S(w_n) получается путем деления амплитуды ,n-ной гармоники на полосу частот f₁ отделяющую соседние линии дискретного спектра. Следовательно S(w_n) имеет смысл плотности амплитуд и обладает размерностью .

К этому результату можно прийти еще и следующим образом. Составив отношение амплитуды n-ной гармоники А_п к частотному интервалу между двумя соседними спектральными линиями, т.е. к частоте повторения f₁ и устремив период Т к бесконечности, можно заметить, что это отношение, т. е. , остается неизменным, поскольку с увеличениемТ как , так и f_i одинаково быстро уменьшаются. В пределе, при Т®¥, это отношение и приобретает смысл спектральной плотности непериодической функции.

Из соотношения вытекает следующее важное положение. Огибающая сплошного спектра (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции (полученной из непериодической путем продолжения ее с периодом Т) совпадают по форме и отличаются только масштабом

.

Спектральная плотность S(w) обладает всеми основными свойствами комплексной амплитуды . По аналогии с можно написать следующее соотношение:

,

где A(w) и B(w) – соответственно действительная и мнимая части спектральной плотности; S(w) и y(w) – амплитудная и фазовая характеристики спектральной плотности.

Из вытекают следующие выражения для A(w) и B(w)

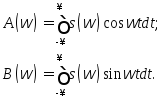
Модуль и фаза спектральной плотности определяются из

Как и в случае ряда Фурье, модуль спектральной плотности четная функция частоты, а фаза – нечетная w.

Используя нетрудно привести интегральное преобразование к тригонометрической форме:

Из условия четности модуля и нечетности фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором– нечетной относительно w. Следовательно, второй интеграл равен нулю и, окончательно,

Из последнего преобразования видно, что при переходе от комплексной формы к тригонометрической отпадает необходимость интегрирования в области отрицательных значений w. Обычно этот переход целесообразен в конце анализа; все промежуточные выкладки при применении интеграла Фурье удобнее и проще производить на основе комплексной формы .

Следует подчеркнуть, что определяемая формулой фазовая характеристика спектральной плотности y(w) дает величину начальной фазы гармонической составляющей частоты w относительно косинусоидального колебания. Если при какой-либо частоте w фаза y(w), то соответствующая этой частоте гармоника имеет вид coswt. Если , то гармоника имеет вид sinwt.

Интегральные преобразования и очень удобны для анализа передачи непериодических сигналов через линейные цепи. Можно написать следующие очевидные соотношения для сигнала s_вх(t) на входе и сигнала s_вых(t) на выходе линейного четырехполюсника:

/

Существенным удобством при использовании интеграла Фурье является возможность получения выражения для выходного сигнала в замкнутой форме, а не в виде медленно сходящегося ряда