
- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
2.12. Координаты единичного вектора. Направляющие косинусы
Если задан
вектор![]() ,
то орт направления, т.е. вектор
,
то орт направления, т.е. вектор![]() ,
определяется из формулы:
,
определяется из формулы: .
Длина вектора равна:
.
Длина вектора равна:![]() ,
,
тогда
 или
или
 .
.
|
Поместим вектор
| |
|
Рис.11 |
координат
направляющими
углами вектора
направляющими
косинусами вектора
Пусть вектор
на рис.11
Аналогично: |
|
Тогда
Отсюда
| |
3. Скалярное произведение двух векторов
Определение. Скалярным произведением двух векторов называется
|
|
число,
равное произведению длин векторов
на косинус угла между ними
Теорема 2.
Если векторы
|
| ||||||||||||||||||
|
Дано:
Доказать:
Доказательство.
Разложим векторы | ||||||||||||||||||||
|
|
| ||||||||||||||||||
|
| ||||||||||||||||||||
2. Свойства скалярного произведения.
|
10.
| ||
|
20.
| ||
|
30.
| ||
|
40.
| ||
|
В векторной форме |
В ДОСК | |
|
50.
|
50.
| |
|
60.
|
60.
| |
|
70.
условие ортогональности. |
70.
| |
|
80.
|
80.
| |
|
|
90.
| |
|
Докажем
сойство 7.
Теорема 3. Скалярное
произведение векторов равно нулю
тогда и только тогда, когда эти векторы
ортогональны т.е. | ||
Дано:
Доказать:
Доказательство. Так как по условию
Следовательно,
угол
|
Дано:
Доказать:
Доказательство.
Так как по
условию | |
Физический смысл скалярного произведения.
|
Пусть
материальная точка движется прямолинейно
от точки
| ||
|
под
действием постоянной силы
| ||
|
| ||
|
|
движения. Тогда работа, совершаемая при этом движении, равна:
|
|



 .
.
 ,
, .
. или
или .
. ,
, ,
,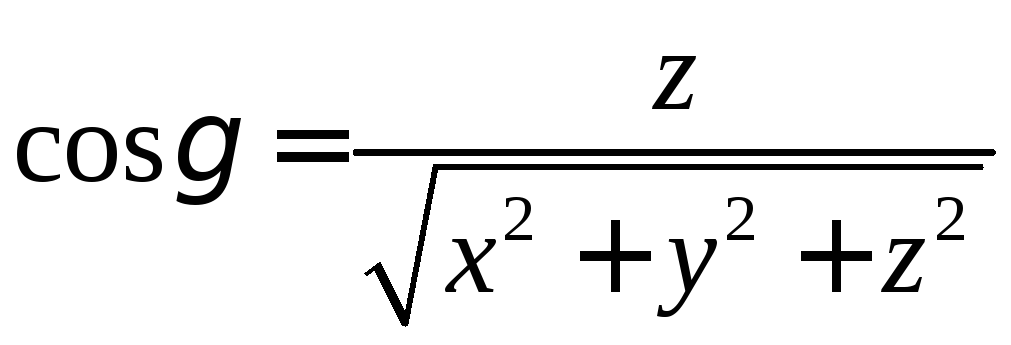 .
.

 .
. .
. .
.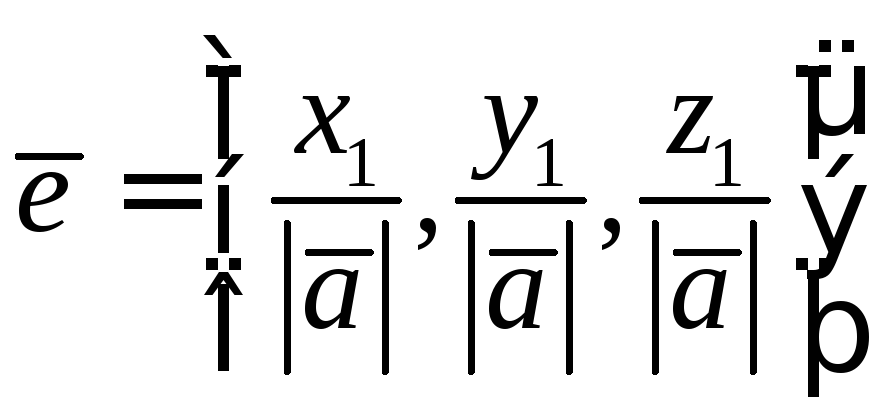
 90.
90. .
.