3. Методические указания к решению задач индивидуальных домашних заданий (идз)

1. Линейные операции над векторами

Задача 1. В равнобедренной трапеции ABCD угол АDС равен ,,исередины сторонисоответственно. Выразить векторычерезиорты направленийи.

Решение.

Выберем треугольник, в который входит неизвестный вектор, а два других либо даны, либо их можно найти. Из имеем:. Так каки, то,. , то . Тогда

5. Из имеем:;.

   Для нахождения вектора определим его длину. Из условия , следовательно. Тогда , т.е. .

6. Из :.

, .

, т.е. .

7. Из :

, .

Задача 2. Найти орт биссектрисы угла между двумя векторами и.

Решение. Перенесём векторы ив одну точку. Диагональ четырёхугольника

совпадает с биссектрисой угла, если четырёхугольник ромб. Если найти орты направлений, то получим векторы иединичной длины. Построим наипараллелограмм, который будет являться ромбом.

Следовательно, диагональ делит угол ромба пополам, т.е. является биссектрисой угла. Найдём и. Векторыиимеют координаты:, тогда,,,

.

Задача 3. Образуют ли векторы базис в пространстве? Если да, то найти линейную зависимость вектораот векторов,и.

Решение. Три вектора образуют базис в тогда и только тогда, когда они линейно независимы. Аналитически это означает, что уравнениес неизвестнымиимеет единственное нулевое решение, а это означает, что определитель системы. Составим систему:

, т.е.

,

следовательно, система имеет единственное решение , тогда,

векторы линейно независимы и образуют базис. Поэтому, вектор можно разложить по данному базису единственным образом, т.е.:

. Решим систему методом Гаусса.

.

Получим .

2. Скалярное произведение двух векторов и его приложения

Задача 4. Найти вектор , перпендикулярный векторам,и, где.

Решение. Условие задачи запишем в виде векторных уравнений.

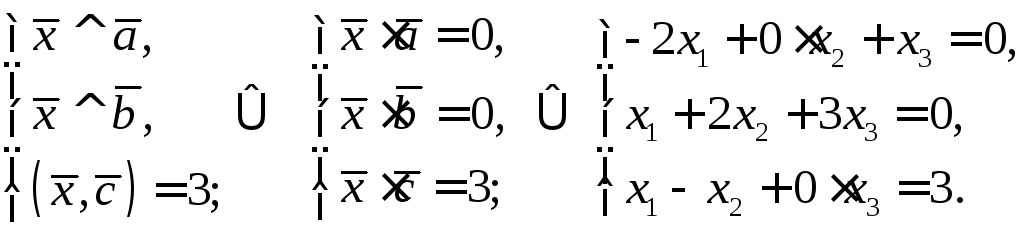Решим систему

уравнений методом Гаусса.

.

Таким образом, вектор .

Задача 5. Найти вектор , коллинеарный вектору

и, удовлетворяющий условию , где.

Решение.

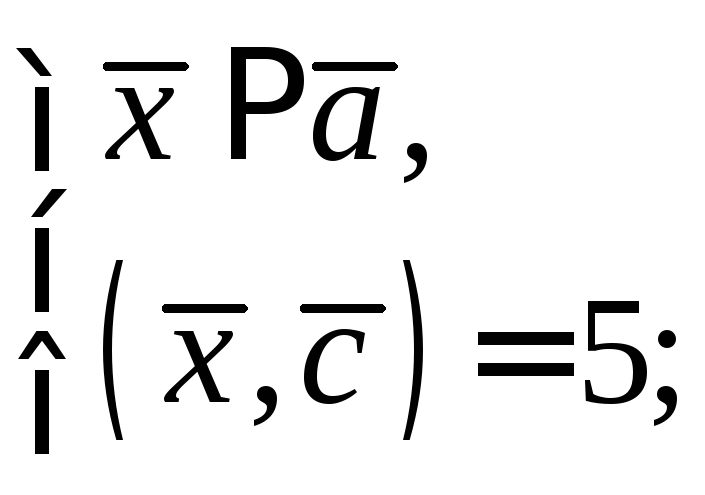
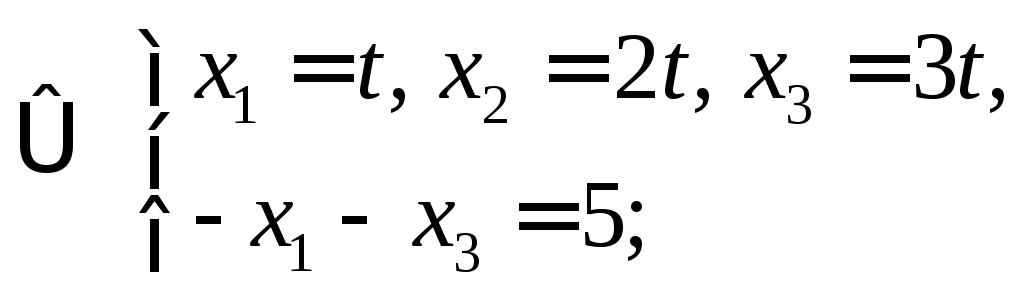
и вектор .

Задача 6. Вычислить проекцию вектора на вектор, где , .

Решение. . Найдём вектор.

,

и

Задача 7. Материальная точка под действием сил иперемещается из точкив точку.

Найти работу, совершаемую при этом перемещении.

Решение. , гдеравнодействующая сили, т.е..

Вектор .

Следовательно, работа равна .

3. Векторное произведение двух векторов и его приложения

Задача 8. Упростить выражение .

Решение. Найдём векторные произведения для этого раскроем скобки, т.е.

.

Задача 9. Упростить выражение , если

.

Решение. Используя схему, получим, например, , кроме того .

.

Задача 10. На материальную точку действуют силы,,. Определить величину и направляю-

щие косинусы момента равнодействующей сил относительно точки .

Решение. , гдеравнодействующая сил.

, плечо, т.е.

вектор .

.

.

Направляющие косинусы момента есть координаты орта:

.

Задача 11. Треугольникпостроен на векторахи, где. Найти высоту, опущенную из вершины.

Решение. . С другой стороны,, следовательно. Найдём

.

.

.