Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с

УДК 53 (075.8) ББК 22.3 я 73 O-28

А в т о р ы :

А.Н. Варава, М.К. Губкин, Д.А. Иванов, И.В. Иванова, А.В. Кириченко, А.Н. Седов, В.С. Спивак

Р е ц е н з е н т ы:

доктор физ.-мат. наук. проф. В.А. Твердислов (МГУ); доктор физ.-мат. наук. проф. В.И. Лобышев (МГУ); доктор физ.-мат. наук. проф. Д.Л. Широчин (МГГУ); канд. техн. наук, доц. С.М. Крейнин (МГГУ)

Общая физика [Электронный ресурс] : учебное пособие для О-28 вузов / А.Н. Варава, М.К. Губкин, Д.А. Иванов и др.; под ред.

В.М. Белокопытова. — М.: Издательский дом МЭИ, 2016. — Загл. с тит. экрана.

ISBN 978-5-383-00999-4

Изложены теоретические материалы по механике, молекулярной физике и термодинамике, электричеству и магнетизму, по оптике и основам квантовой механики. Приведены примеры решения некоторых нестандартных задач, позволяющих глубже понять изучаемый материал.

Настоящее электронное издание подготовлено на основе одноименного печатного издания (2-е изд., стереот.), вышедшего в Издательском доме МЭИ в 2016 году.

Для студентов первого и второго курсов энергетических вузов, а также других учебных заведений.

УДК 53 (075.8) ББК 22.3 я 73

2

ПРЕДИСЛОВИЕ

Настоящее учебное пособие содержит 30 глав, в которых излагается теоретический материал по основным разделам курса общей физики, соответствующим действующей программе курса для технических вузов и охватывающим все основные вопросы этой программы.

Основное содержание предлагаемого пособия составляет расширенное изложение лекций по физике, которые в течение 30 лет читались студентам различных факультетов в Московском энергетическом институте на кафедре общей физики и ядерного синтеза. Данный материал входил в ранее изданные Издательством МЭИ конспекты лекций по отдельным разделам дисциплины.

Учебное пособие рассчитано в первую очередь на студентов первого и второго курсов и может быть широко использовано для самостоятельной работы, так как включает в себя не только изложение теоретического материала, но и примеры решения типовых задач. Главное внимание обращается на выяснение физического смысла и содержания основных положений и понятий физики. В отдельные главы выделены примеры решения некоторых нестандартных задач по разделам «Механика», «Молекулярная физика и термодинамика», «Электричество и магнетизм». Данные задачи позволят студентам глубже понять изучаемый материал, развить навыки физического мышления и умения самостоятельно ставить и решать физические задачи.

Учебное пособие может оказаться полезным не только для студентов энергетических вузов, но и других учебных заведений.

Авторы считают своим долгом выразить благодарность коллегам по кафедре общей физики и ядерного синтеза, в том числе А.В. Славову, В.А. Касьянову, С.Д. Федоровичу и А.Т. Комову за ряд ценных замечаний, высказанных при обсуждении рукописи, а также И.В. Авиловой за большую техническую работу по подготовке книги к изданию.

Предложения и замечания по содержанию книги просим направлять по адресу: 111250, Москва, Красноказарменная ул., д. 14, НИУ МЭИ, кафедра общей физики и ядерного синтеза.

Авторы

3

Р а з д е л I

МЕХАНИКА

Этот раздел физики рассматривает простейшую форму движения материи: перемещение одних тел относительно других и изменение формы тела. Основные законы механики были в значительной степени выяснены Г. Галилеем (1564—1642) и окончательно сформулированы И. Ньютоном (1643—1727). Механика Галилея — Ньютона получила название классической. Ее законы и выводы справедливы при одновременном выполнении двух условий:

1) рассматриваемые тела — макроскопические;

света в вакууме (универсальная, т.е. мировая постоянная). Классическая механика делится на три части: кинематику, дина-

мику и статику.

Кинематика изучает движение тел в пространстве и времени без рассмотрения причин, вызывающих это движение.

Динамика изучает движение тел в связи с причинами (силами), которые обусловливают тот или иной характер движения.

Статика изучает равновесие тел и в нашем курсе не рассматривается.

Г л а в а 1

КИНЕМАТИКА

В механике широко используют две модели: материальную точку и материальное тело. Материальная точка — это тело нулевых размеров, т.е. абстрактная физическая модель. Любое тело можно представить как совокупность материальных точек. Материальное тело может состоять из дискретных точек или быть сплошным.

Абсолютно твердым телом называется такое тело, расстояние между любыми двумя точками которого не изменяется.

Важным вопросом в кинематике является задание положения тела в пространстве. Свободное пространство является однородным (в нем нет точек, обладающих особыми свойствами) и изотропным

4

(в нем нет выделенных направлений). Поэтому в свободном пространстве нельзя определить положение материальной точки или тела.

Телом отсчета называется абсолютно твердое тело, относительно которого можно задать положение произвольного объекта в пространстве.

1.1. Система координат. Система отсчета. Способы задания положения точки в пространстве

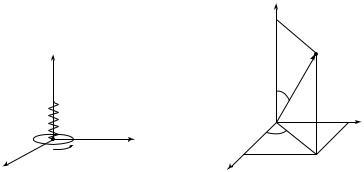
Все физические процессы протекают в пространстве и во времени. С телом отсчета связывают систему координат, которая позволяет указать «адрес» материальной точки или тела, т.е. задать положение точки или тела в пространстве. Время — мера длительности процессов. Для его отсчета требуются часы. Тело отсчета, система координат и часы образуют систему отсчета. Мы будем использовать декартову прямоугольную (исключительно правую) систему координат (рис. 1.1). В такой системе координат ось OZ направлена в сторону поступательного движения правого винта, который вращается от оси ОХ к оси OY по кратчайшему углу. Она не является единственно возможной. В нашем курсе будут использованы два способа задания положения точки в пространстве: векторный и координатный.

Векторный способ. Положение материальной точки М задается с

помощью радиуса-вектора ºr , который проводится из начала коор-

динат в точку М (рис. 1.2). Для того, чтобы задать радиус-вектор ºr , необходимо указать:

1) начало системы координат — т. О ;

5

2)модуль ºr ;

3)направление радиуса-вектора в пространстве, определяемое двумя независимыми углами.

Используя векторы единичной длины, сонаправленные с осями

Для случая, изображенного на рис. 1.2, можно записать:

rx = x ; ry = y ; rz = z .

Координатный способ. Положение материальной точки М задается с помощью координат x, y, z и записывается в виде М(x, y, z).

З а м е ч а н и е . Минимальное число независимых параметров, которое полностью определяет положение физической системы в пространстве, называется числом ее степеней свободы. Можно сказать, что материальная точка имеет три степени свободы.

1.2. Понятие траектории. Кинематический закон движения материальной точки.

Вектор перемещения. Путь

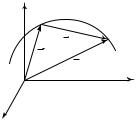
Линия, которую описывает движущаяся точка в пространстве, называется траекторией. Вид траектории зависит от выбора системы отсчета. Рассмотрим равномерное движение точки по радиусу равномерно вращающегося диска от центра к краю (рис. 1.3). Отно-

сительно системы координат (X ′, Y ′, Z ′) , связанной с вращающимся диском, траектория точки будет прямой линией. Относительно системы координат (X, Y, Z ), связанной с Землей, траектория точки будет спиралью Архимеда.

X

Рис. 1. 3

6

ческий закон ее движения имеет вид: ºr = ºr (t) , а при координатном способе он может быть записан в виде:

x = x(t);

y = y(t); (1.2)

z = z(t).

Если из соотношений (1.2) исключить время t, то получим уравнение, которое будет описывать траекторию материальной точки.

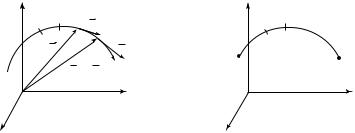
Рассмотрим движение точки по траектории L (рис. 1.4). Пусть в момент времени t точка находилась в положении 1, определяемом

начального положения точки в конечное, называется вектором

перемещения равен изменению (или приращению) радиуса-вектора.

Расстояние между точками 1 и 2, измеренное вдоль траектории, называется путем S.

При стремлении t к нулю конечное приращение радиуса-век-

тора dºr .

Направление вектора dºr будет совпадать по направлению с еди-

ничным вектором ºτ , направленным по касательной к траектории в сторону движения точки.

7

1.3. Скорость. Нахождение пути. Ускорение

Разобьем траекторию L материальной точки на бесконечно малые участки длиной d L (рис. 1.5). Каждому участку траектории d L будет

соответствовать перемещение dºr . Разделим это перемещение на промежуток времени dt, за который материальная точка проходит

где точкой сверху обозначена производная по времени.

Так как вектор dºr направлен по касательной к траектории в сто-

º

рону движения точки, то и вектор мгновенной скорости v направлен туда же. С учетом выражения (1.1) вектор мгновенной скорости может быть представлен в виде

Таким образом, компоненты вектора скорости определяются как соответствующие производные:

Тогда модуль скорости может быть найден из выражения:

v 2 = vx2 + vy2 + vz2 .

Равномерным называется движение с постоянной по модулю

Определим путь, проходимый телом за время t при движении по произвольной траектории из положения 1 в положение 2 (рис. 1.6).

8

Разобьем траекторию на такие малые участки (в дальнейшем называемые элементарными), чтобы можно было считать скорость на этих участках неизменной. Тогда длина траектории i-го участка (путь) будет выражаться формулой

Li = vi ti ,

где vi — модуль скорости на i-м участке; ti — время его прохож-

дения.

Весь путь можно найти как сумму длин всех элементарных участков. При этом путь будет определен тем точнее, чем меньше рас-

Важной векторной кинематической величиной является ускорение — производная мгновенной скорости по времени, которое характеризует быстроту изменения вектора скорости:

В проекциях на оси координат получим следующие выражения:

1.4. Кинематический закон движения материальной точки с постоянным ускорением

Если вектор ускорения остается постоянным по модулю и направлению, то такое движение называется равнопеременным.

9

где ºr 0 — радиус-вектор, определяющий положение тела в момент

времени t = 0.

Использовав (1.2), запишем законы изменения координат тела:

z= z0 + v0zt + azt 2⁄ 2.

1.5.Нормальное и тангенциальное ускорения

Вобщем случае направление вектора ускорения тела неизвестно. Для его нахождения выберем в каждой точке траектории два единич-

º

ектории в сторону движения точки, а вектор n — по нормали в сторону вогнутости траектории (рис. 1.7). В конкретных задачах бывает

º

удобно рассматривать проекции вектора ускорения a на выбранные таким образом направления.

10