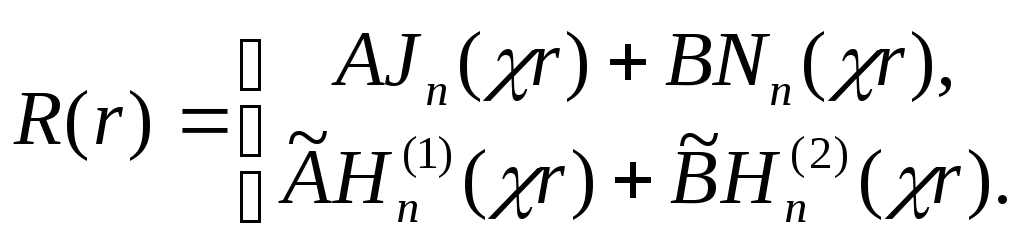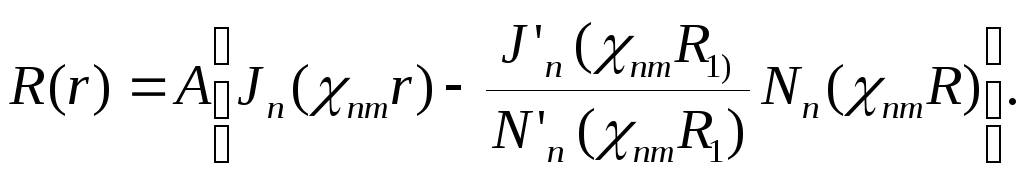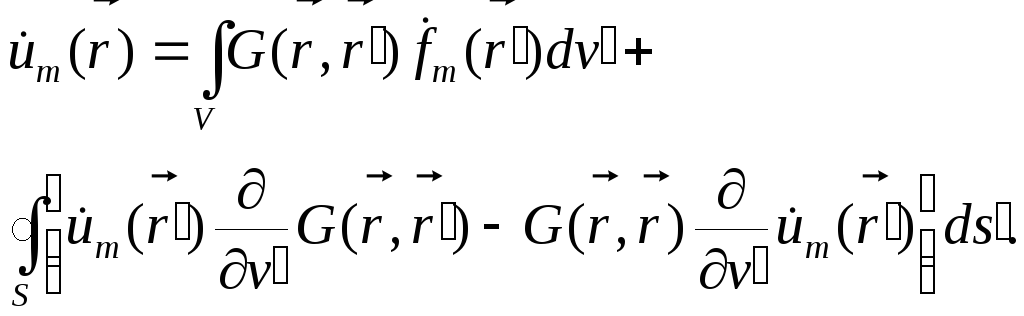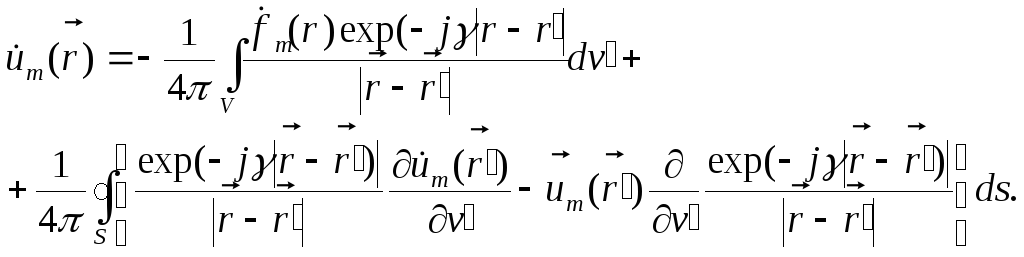6.2. Задачи в цилиндрических координатах

Двумерное уравне­ние Гельмгольца в цилиндрических координатах имеет следующий вид:

(6.24)

Решение этого уравнения будем искать как произведения T(r,α) = R(r)A(α).

Рядом не слишком сложных и логичных операций соотношение (6.24) можно разбить на два отдельных уравнения:

	(6.25)
	(6.26)

Первое уравнение (6.25) - это уравне­ние Бесселя при у = R, х = χr. Его общее решение запишем в следующей форме:

(6.27)

Решение второго уравнения, (6.26), также известно:

(6.28)

Таким образом, найден общий вид решения Т = RA уравнения в ци­линдрических координатах, содержащий ряд неопределенных кон­стант.

Для анализа распространения поля в круглом волноводе необходимо решить две краевые задачи (5.8) и (5.9) в цилиндрических координатах для кругового контура диаметром R. Собственные функции и собственные значения решения первой краевой задачи (5.8) имеют следующий вид:

	(6.29)

Решения второй краевой задачи (5.9) записываются так:

	(6.30)

В заключение рассмотрим кольцевую область. Она имеет два контура в виде окружности на расстоянии R₁ и R₂ от центра.

Начнем с решения первой краевой задачи (5.8). Уравнение для собственных значений запишем в следующем виде:

(6.31)

Для получения полных собственных функций воспользуемся следующим выражением:

(6.32)

Его надо подставить в первую строчку (6.29) вместо . Таблицы дляχ_nm имеются в различ­ных справочниках.

Уравнение относительно χ во второй краевой задаче (5.9) для той же кольце­вой области записывается в виде:

(6.33)

Вместо (6.32):

(6.34)

где χ_nm - корни (6.33); они приводятся в справочниках.

Для получения полных собственных функций надо внести R(r) (6.34) вместо в (6.30), отбросив А.

7. Математический аппарат излучения радиоволн

7.1. Интегрирование неоднородного уравнения Гельмгольца

Начнем с рассмотрения неоднородного скалярного уравнения Гельмгольца:

(7.1)

Оно отличается от уравнения Пуассона наличием второго члена в левой части.

Как и при интегрировании уравнения Пуассона, в данном случае вводится функция Грина G(r, r'). Она является решением исходного уравнения (7.1) при правой части в виде дельта-функции Дирака:

(7.2)

Функция Грина имеет вид:

(7.3)

Используя, вторую формулу Грина, получаем на основе (7.1) и (7.2) интегральное соотношение:

(7.4)

В процессе преобразований использована симметрия функции Грина относительно аргумента r и r', т. е. возможность замены в формуле (7.3) r на r' и обратно.

Внося выражение функции Грина (7.3) в решение (7.4), получаем:

(7.5)

Для нас наиболее интересен случай, когда решение ищем во всем безграничном пространстве, так что граница S области V относится в бесконечность. При этом функция f_m(r) отлична от нуля только в некоторой ограниченной области.

Выделим класс решений, для которого при отнесении в бесконечность границы S поверхностный интеграл в решении (7.5) исчезает. Выделенный класс решений потребует отдельного исследования, которое будет произведено ниже. Пока же отметим, что в рассматриваемом случае из (7.5) следует:

(7.6)

Интегрирование здесь фактически распространяется только на область, в которой f_m(r) ≠ 0. Таким образом, мы получили выражение решения неоднородного скалярного уравнения Гельмгольца (7.1).

Возьмем векторное уравнение:

(7.7)

Рассмотрим его проекции на оси декартовой системы координат. Получим три скалярных уравнения типа (7.1), решения которых при оговоренных условиях выражаются формулой (7.6). Складывая их, запишем справедливое при тех же условиях представление решения неоднородного векторного уравнения Гельмгольца (7.7):

(7.8)