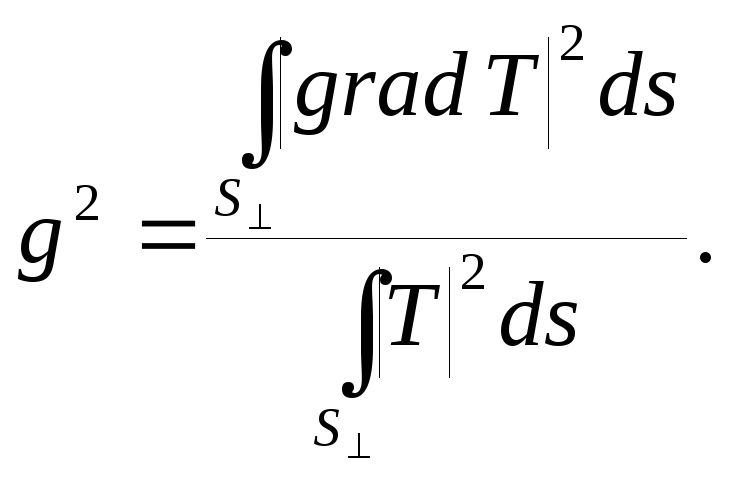5.1. Задачи для продоль­но-однородных структур

Рассмотрим один класс решений однородного скалярного уравнения Гельмгольца (4.17):

(5.1)

Рассмотрим пространственную структуру, однородную в направлении z. Однородной называется структура, у которой распределение поля во всех ее сечениях плоскостями z = const тождественны. Примеры таких структур показаны на рис. 5.1.

Будем искать функцию и внутри и (или) вне обобщенного цилиндра (а) или при нали­чии нескольких аналогичных подобластей (б). Волновое число γ может принимать в под­областях разные постоянные значения. На их границах комплексная амплитуда удовлетворяет некоторым условиям. Например, могут рассматриваться решения уравнения (5.1) внутри цилиндрической области (рис. 5.1,а) при граничном условии u_m = 0. Предположим, что решение для комплексных амплитуд можно представить в виде про­изведения двух неизвестных функций разных аргументов: . В результате подстановки этого представления в уравнение (5.1) получаем:

Рис. 5.1. Продольно-однородные структуры

Разделим все члены на произведение TZ и введем следующее обозначение:

(5.2)

В результате получим:

(5.3)

В этом уравнении разделены переменные, так как оба сла­гаемых - функции разных аргументов. Поэтому из­менение координаты z не может повлиять на первый член, и он сохра­нит при этом постоянное значение. А это означает, что остается постоянным и второй член, т. е. он равен некоторой константе. Обозначим ее h²:

Очевидно, что первый член равен противоположной константе -h². Эти рассуж­дения приводят от уравнения (5.3) к двум независимым урав­нениям:

	(5.4)
	(5.5)

Если решения Z и Т найдены, то найдено и решение исходного уравнения Гельмгольца (5.1) u_m = TZ. Этот метод решения дифференциальных уравнений называется методом разделения переменных.

Таким образом, нам удалось выяснить некоторые общие черты решений уравнения Гельмгольца в классе продольно-однородных структур.

Вид ре­шений обыкновенного дифференциального уравнения (5.4) хорошо известен. Выберем экспоненциальную форму представления функции Z:

где А и В - неопределенные кон­станты. Поэтому искомое решение примет вид:

(5.6)

Это неоднородные волны, поскольку их амплитуды зависят от поперечных координат х и у. Если h - вещественная величина, то она играет такую же роль, как γ в формуле (4.3). Для комплексного h можно записать следующие соотношения:

(5.7)

Здесь λ_в - длина волны в структуре, v_ф - ее фазовая скорость, а h" - коэффициент затухания. При этом предполагается, что h' > 0, h" > 0.

5.2. Краевые задачи для двумерного уравнения Гельмгольца

Трехмерную задачу о распространении волн в про­дольно-однородной структуре мы свели к рассмотрению двумерного уравнения Гельмгольца (5.5). При этом неизвестна не только функ­ция Т(х, y), но и параметр g². Само по себе уравнение (5.5) не имеет определенных решений. Для его решения необходимо поставить краевую задачу.

Пусть, например, L_┴ - контур по­перечного сечения цилиндра. Условия первой краевой задачи для двумерного уравнения Гельмгольца записываются следующим образом:

(5.8)

Рассмотрим внутреннюю задачу. То есть будем искать решение Т внутри структуры. Эта задача имеет бесконечное множество решений {Т_п}, каждое из которых реализуется при определенном значении пара­метра g². Решения Т_п называются собственными функциями, а со­ответствующие им значения g²_n параметра g² - собственными зна­чениями. Нумерация производится в порядке неубывания собствен­ных значений: g²₁ ≤ g²₂ ≤ g²₃... Если разным собственным функциям соответствуют одинаковые собственные значения, то такие функции на­зываются вырожденными.

Вторая краевая задача для уравнения (5.5) формулируется следующим образом:

(5.9)

Эта задача также порождает систему собственных функций, кото­рым отвечают собственные значения.

Для обеих краевых задач легко полу­чить следующее интегральное соотношение:

(5.10)

Для этого обе части уравнения (5.5) умножаются на Т* и производится интегрирование по поперечному сечению S_┴ структуры. Далее применяется двумерный аналог тео­ремы Грина с заменой V на S_┴, S на L_┴ при φ = φ* = Т. После этого остается только учесть граничное условие первой или второй задачи, что приводит к уничтожению контурного интеграла.

Из формулы (5.10) следует, что собственные значения рассматриваемых задач неотрицательны.

Если фигурирует несколько подобластей, и для каждой из них γ принимает свое значение γ_i, то соответственно этому в уравнении (5.5) возникают разные поперечные волновые числа:

(5.11)

Здесь i - номера подобластей.

Постоянная распростране­ния h является общей для всей продольно-однородной структуры.