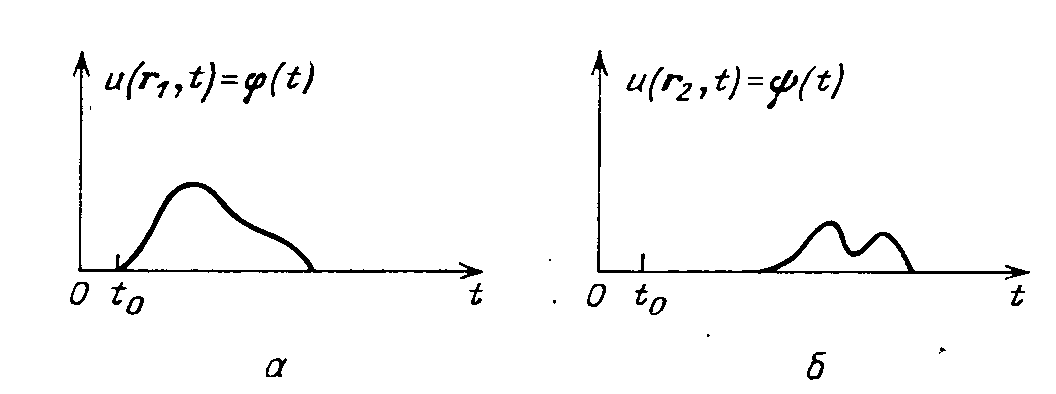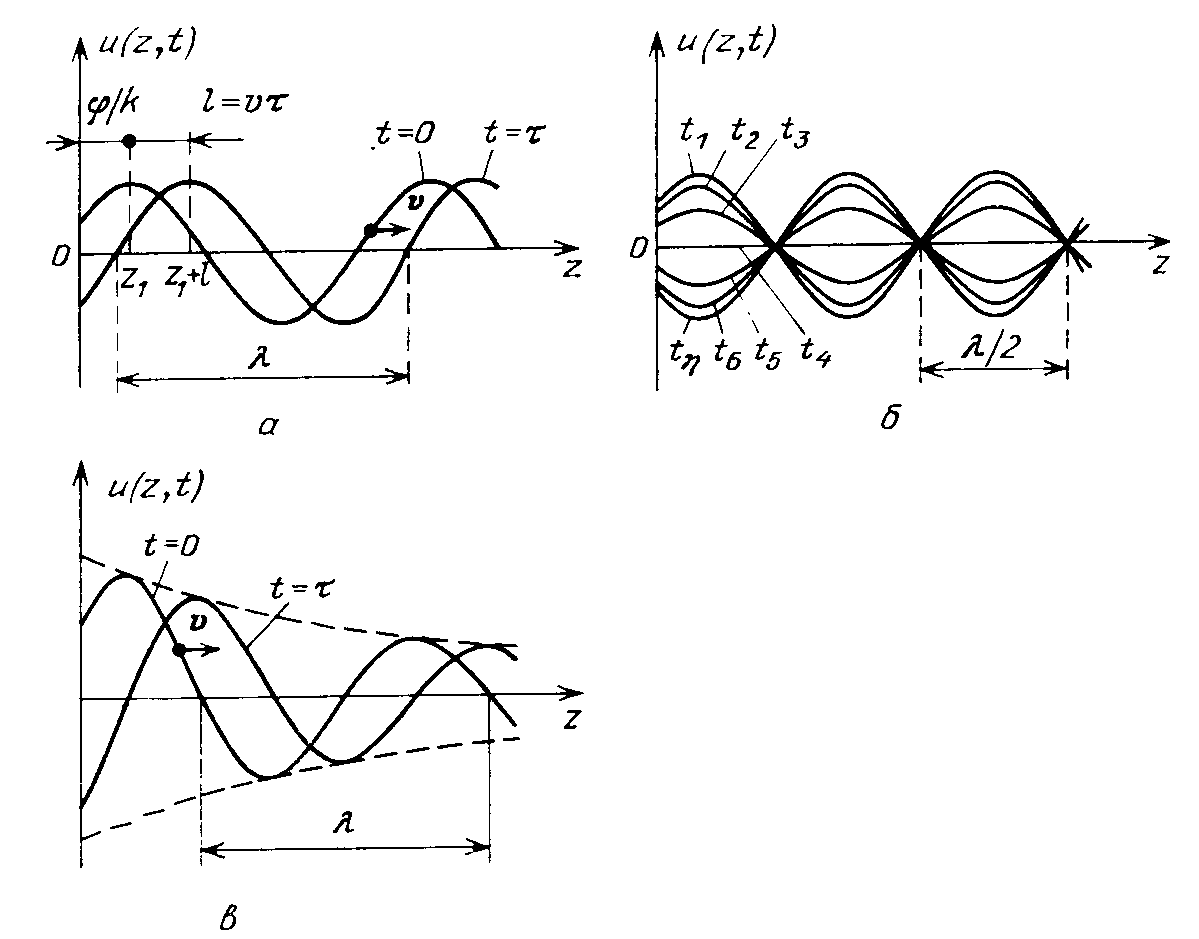4. Общие сведения о волновых процессах

4.1. Введение

В основе математического описания волновых процессов лежат следующие соображения. Пусть в точке М(r₁), мы можем охарактеризовать процесс функцией u(r₁, t) = φ(t) (рис. 4.1,а). В другой, достаточно отдаленной, точке P(r₂) процесс не будет наблюдаться до тех пор, пока он не будет передан средой. Тогда в точке наблюдения будет обнаружен процесс u(r₂, t) = ψ(t) (рис. 4.1,б).

Рис. 4.1. К пояснению понятия волновых процессов

При этом закон зависимости функции u от времени может оказаться измененным. В простейшем случае в точке Р(r₂) будет обнаружено лишь запаздывание того, что происходило в точке М(r₁). При этом ψ(t) = φ(t + τ), где τ - время, требуемое для прохождения пути |r₂ - r₁| = l со скоростью v.

Положим, что в пространстве какие-либо изменения происходят только в направлении z. Тогда в соответствии со сказанным волновой процесс характеризуется функцией:

(4.1)

Пусть при z = 0 эта функция u(0, t) = φ(t) имеет вид, показанный на рис. 4.2,а. Тогда при z = l (рис. 4.2б) процесс будет описываться зависимостью, отличающейся от исходной лишь сдвигом: u(l, t) = u(0, t - l/v).

Рис. 4.2. Распространение волны

Рассмотренный волновой процесс - это плоская однородная волна в не деформирующей ее среде.

Обратимся к рис. 4.2,в. На нем для двух моментов времени t₁ и t₂ построена величина u(z, t) как функция от расстояния z.

Зафиксируем какую-либо фазу процесса, то есть мгновенное значение. На рис. 4.2,а, б, в выбрано значение u = а. Плоскость с любой фиксированной фазой называется фронтом волны. Рассмотрим плоскость z = const. Из рис. 4.2,в видно, что за время τ = t₁ - t₂ она переместилась на расстояние l = vτ.

Распространение волны можно рассматривать и как движение ее фронта. Кривые на рис. 4.2,в, построенные для моментов t₁ и t₂, называют мгновенными снимками процесса.

Как выразить волну, распространяющуюся не в направлении z, а в противоположном? Для этого нужно изменить знак скорости v. Считая величину скорости положительной, мы должны в формуле (4.1) заменить аргумент t - z/v на t + z/v.

4.2. Гармонические волны

Конкретизируем выражение (4.1) для закона гармонических колебаний, описываемых формулой (3.1). В результате получим описание гармонической волны:

(4.2)

Параметр γ = ω/v называется волновым числом, а v - фазовой скоростью.

На рис. 4.3,а построены два мгновенных снимка гармонической волны. При каждом фиксированном времени t величина u(z, t) по формуле (4.2) имеет косинусоидальное пространственное распределение. Его период называется длиной волны. Длина волны - расстояние, на котором фаза изменяется на 2π. Длина воны обозначается символом λ. Таким образом, γλ = 2π. То есть, волновое число может быть выражено и через фазовую скорость и через длину волны:

(4.3)

Учитывая то, что ω = 2πf , получим:

(4.4)

Распространение гармонической волны отображается смещением косинусоиды вдоль оси z со скоростью v. Это иллюстрирует рис. 4.3,а.

Рис. 4.3. Гармонические волны

Пусть навстречу друг другу распространяются две гармонические волны. При этом функция в точке с координатами (z, t) может быть определена по формуле:

(4.5)

Если амплитуды и фазы прямой и обратной волн равны, формула (4.5) примет вид:

(4.6)

Такой процесс называется стоячей волной.

Из рис. 4.3,б видно, что в каждый момент времени имеется неподвижная косинусоида. Ее нули не смещаются вдоль оси z.

С помощью метода комплексных амплитуд для гармонической волны (4.2) можно записать комплексное представление:

(4.7)

где

,

.

В рамках метода комплексных амплитуд волновые числа также могут быть комплексными:

(4.8)

Величина α называется коэффициентом затухания, а β - коэффициентом фазы.

Внесем формулу (4.8) в выражение (4.7) и возьмем действительную часть. В результате получим:

(4.9)

Если α = 0, формулы (4.2) и (4.9) совпадают. Если α > 0, это затухающая волна, изображенная на рис. 4.3,в.

Отношение u(z)/u(z + l) = ехр (αl) показывает, во сколько раз уменьшилась амплитуда волны на пути l. Обычно это отношение логарифмируют и получают величину L, называемую затуханием, которая измеряется в неперах [Нп] либо децибелах [дБ]:

или

(4.10)

Распространение затухающей волны пояснено на рис. 4.3,в. На нем показано смещение мгновенного снимка. При этом экспоненциальная огибающая не смещается. Можно записать следующее выражение для коэффициента фазы:

(4.11)

Здесь фазовую скорость можно рассматривать как скорость смещения фронта с нулевой амплитудой. Длина волны λ, уже не являющаяся периодом и также определяется по нулям.