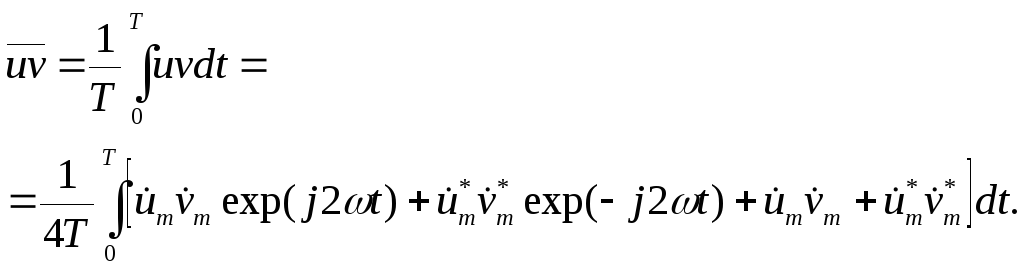3. Метод комплексных амплитуд

3.1. Описание гармонических колебаний

Величина, изменяющаяся по гармоническому закону, может быть представлена в виде:

(3.1)

Здесь u_m – амплитуда колебания, ωt + φ – текущая фаза, φ - начальная фаза.

Периодом Т называется наименьший отрезок времени, обла­дающий следующим свойством: u(t + T) = u(t).

(3.2)

В теории электромагнитного поля используются скалярные и вектор­ные гармонические функции. Скалярная гармоническая функция может быть представлена в следующем виде:

(3.3)

Здесь амплитуда и начальная фаза - функции координат.

Векторная функция в общем случае распа­дается на три скалярных в выбранной системе координат. Напри­мер, в декартовой системе векторная гармоническая функция имеет следующий вид:

(3.4)

Если компоненты вектора имеют одинаковые началь­ные фазы, то эту формулу можно значительно упростить:

(3.5)

Здесь V_m = x₀V_mx + y₀V_my + z₀V_mz, φ = φ_x = φ_y = φ_z.

В теории гармонических колебаний применяется метод комплексных амплитуд. При его использовании в выражениях типа (3.1), (3.3) - (3.5) вместо тригонометрических функций употребляются экспоненциальные. Например, вместо u формулы (3.1) можно записать:

(3.6)

Здесь

- комплексная амплитуда.

Комплексные величины и функции обозначаются точкой сверху.

Согласно формуле Эйлера действительная гармоническая функция связана с комплексной амплитудой соотношением:

(3.7)

Из формулы Эйлера вытекает также следующее соотношение:

(3.8)

Здесь звездочка означает комплексное сопряжение.

В векторном варианте формула (3.4) принимает вид:

(3.9)

Комплексная амплитуда, входящая в формулу (3.9), может быть записана в следующем виде:

(3.10)

3.2. Средние значения

Для периодической функции от времени сред­ним значением называется интеграл от 0 до Т, деленный на период.

Очевидно, что среднее значение от функции вида (3.1) равно нулю. Среднее от квадрата гармонической величины определяется следующим соотношением:

(3.11)

Таким образом, результат усреднения оказалось возможным выразить через комплексные амплитуды. Интеграл в формуле (3.11) легко взять, преобразовав подынтегральное выражение с помощью формулы (3.8).

В дополнение к функции u введем функцию v = v_mcos(ωt+ψ) и найдем среднее от их произведения:

Два первых слагаемых в квадратных скобках колеблются с удвоенной частотой. Интегралы от них дадут нуль. С учетом этого получим:

(3.12)

Аналогичные формулы для векторных величин имеют следующий вид:

	(3.13)
	(3.14)
	(3.15)

Здесь W - векторная функция, подобная V.

3.3. Разложение Фурье для комплексных амплитуд

Разложение периодической функции в ряд Фурье можно записать в следующем виде:

(3.16)

Это же выражение можно представить в комплексной форме:

(3.17)

Здесь

Коэффициенты ряда (3.17) - комплексные амплитуды, а члены - комп­лексные представления гармонических колебаний с частотами nω.

В случае произвольной временной зависимости функции запишем ее разло­жение в интеграл Фурье:

(3.18)

Спектральная плотность u(ω) имеет смысл комплексной амплитуды.