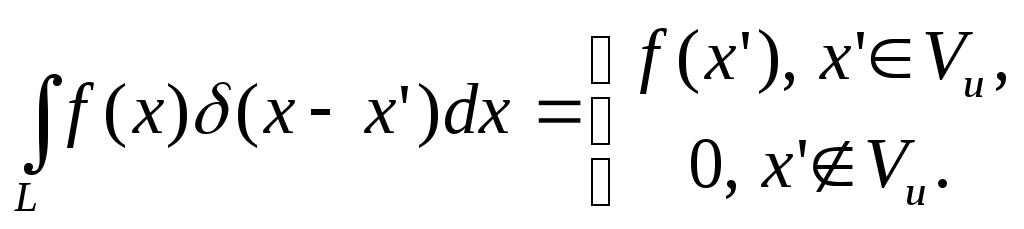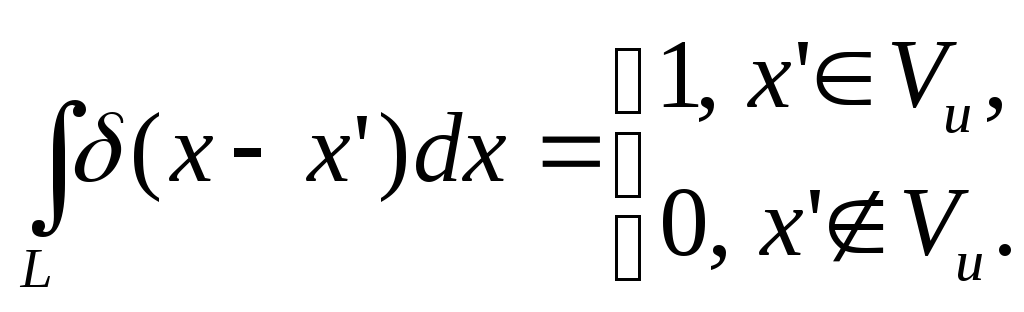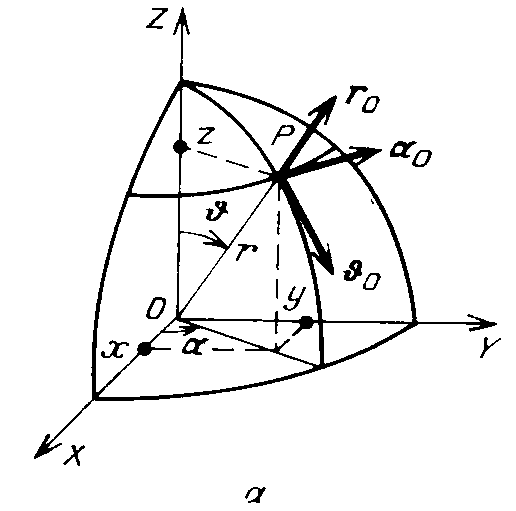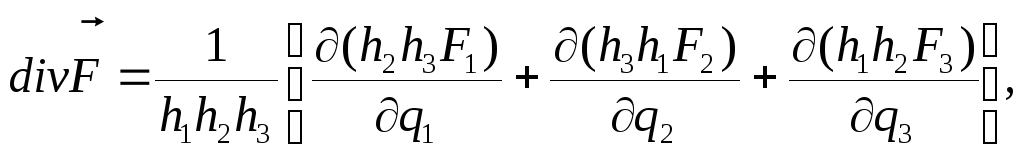1.4. Интегральные формулы векторного анализа

Теорема Остроградского-Гаусса

(1.33)

Теорема Стокса:

(1.34)

Теорема Грина (первая формула)

(1.35)

Теорема Грина (вторая формула)

(1.36)

Аналог теоремы Остроградского - Гаусса для ротора:

	(1.37)

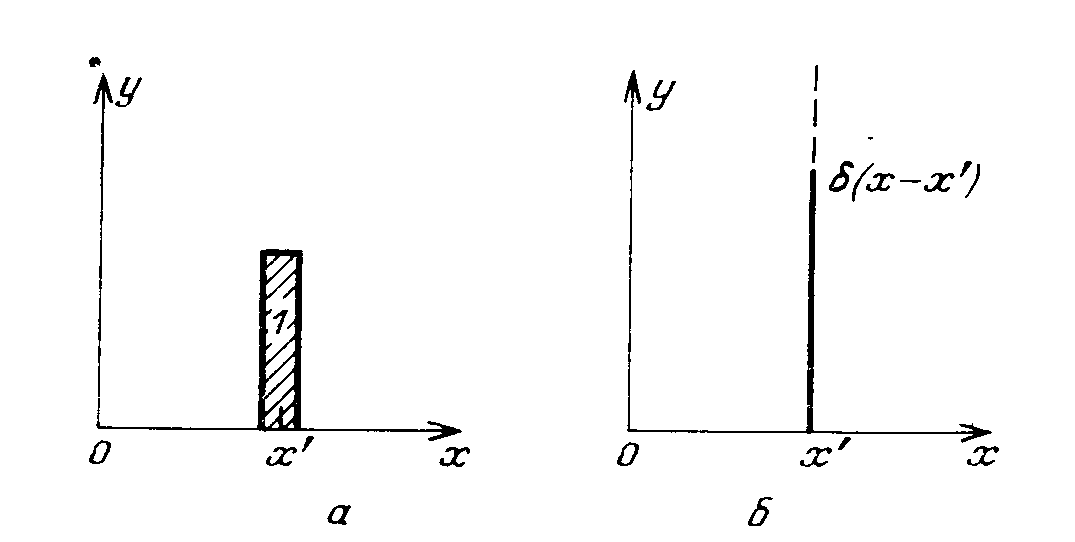
Рис. 1.6. Дельта-функция Дирака

Все выписанные соотношения имеют характер формул интегрирования по частям. При этом объемный интеграл сводится к интегралу по замкнутой границе в виде поверхности S, а поверхностный - к интегралу по замкнутому контуру L.

1.5. Дельта-функция Дирака

Дельта-функция Дирака вводится следующим образом. Рассмотрим прямоугольный импульс площадью равной единице. Он изображен на рис. 1.6,а. Устремим ширину импульса к нулю, сохраняя его площадь постоянной. В результате получим функцию, значение которой не ограничено в точке x' (рис. 1.6,б), а во всех остальных точках равно нулю. Это и есть дельта-функция Дирака, которая обозначается δ(x - x').

Можно утверждать, что для всякой обычной функции f(x) будет справедливо равенство:

(1.38)

Равенство (1.38) является определением дельта-функции посредством функционала. В частности, при f(x) = 1 получим:

(1.39)

Определение (1.38) обобщается на трехмерные области следующим образом:

(1.40)

В этой записи точка задается при помощи радиус-вектора r. В качестве частного случая можно взять f(r) = 1 и получить аналог формулы (1.39).

2. Системы координат

2.1. Градиент длины направленного отрезка

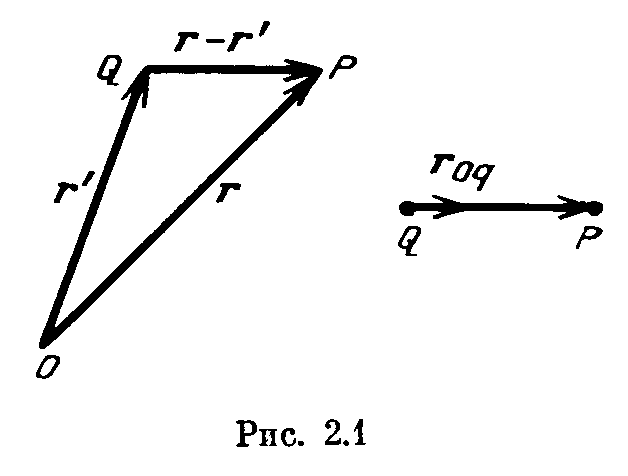
Рис. 2.1. Определение расстояния между точками

Рассмотрим способ определения переменного расстояния между двумя точками Р и Q (рис. 2.1) Положение этих точек описывается радиус-векторами r и r'. Представим эти радиус-векторы в декартовой системе координат с началом в точке 0:

Тогда длина направленного отрезка QP = r - r’ определяется следующим выражением:

Градиент этого скаляра можно определить с помощью формулы (1.14):

(2.1)

Здесь символом r_0Q обозначен орт с направлением r - r'. Расстояние |r - r'| - это функция положения точки Р при фиксированной точке Q.

Если зафиксировать точку Р, расстояние |r - r'| необходимо рассматривать как функцию координат х', у', z’. Градиент по этим координатам записывается в виде:

(2.2)

Штрих, отмечающий градиент, используется для обозначения операции по штриховым координатам.

В дальнейшем встретятся такие скалярные функции от |r - r'|, как |r - r'|^-1 и |r - r'|^-2. Вычисляя для них grad или grad', следует использовать формулу (1.29) вместе с формулами (2.1) или (2.2).

2.2. Операции векторного анализа в криволинейных координатах

Обозначения криволинейных ортогональных координат и относящихся к ним величин приведены в таблице 2.1.

Таблица 2.1

Обозначения элементов криволинейных ортогональных систем координат

Номер координаты	1	2	3
Координата	q1	q2	q3
Орт	e1	e2	e3
Метрический коэффициент	h1	h2	h3

Метрические коэффициенты (коэффициенты Лямэ) участвуют в соотношениях вида dl_i = h_idq_i, где dq_i - дифференциал координаты, a dl_i - дифференциал длины по этой координате.

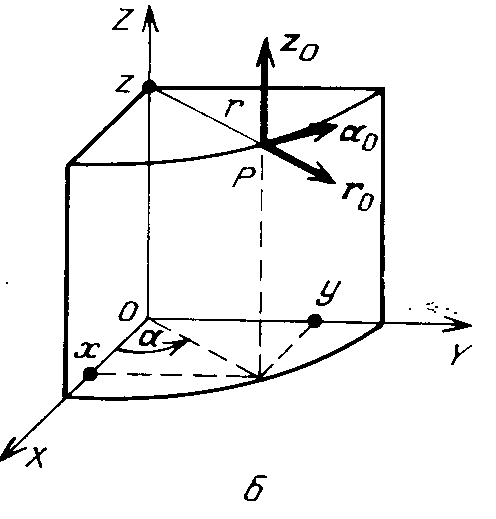
Две наиболее распространенные криволинейные системы координат, сферическая и цилиндрическая, изображены на рис. 2.2. Они показаны вместе с декартовой системой, которая указывает начало отсчета углов. Из рис. 2.2,а видно, что для сферической системы координат h₂ = r есть радиус дуги угла υ, a h₃ = г sin υ - радиус дуги угла α, проходящей через точку Р. Для цилиндрической системы координат (рис. 2.2,б) h₂ = r есть радиус дуги угла α.

Рис. 2.2. Сферическая (а) и цилиндрическая (б) системы координат

В таблице 2.2 приведены обозначения элементов этих систем.

Таблица 2.2

Основные криволинейные координаты

i	Сферические координаты			Цилиндрические координаты
	1	2	3	1	2	3
qi	r	υ	α	r	α	z
ei	r0	υ0	α0	r0	α0	z0
hi	1	r	r sin υ	1	r	1

Смысл метрических коэффициентов понятен из рисунка. Орты по угловым координатам обозначаются так же, как и углы (например, орт υ₀ для координаты υ). Это единичные векторы, направленные по касательной к соответствующим дугам в сторону возрастания углов.

Координаты точки, определенные в разных системах, связаны простыми и очевидными соотношениями:

Декартова и цилиндрическая системы координат:
	(2.3)			(2.4)		(2.5)
	(2.6)		(2.7)

Декартова и сферическая системы координат:
	(2.8)					(2.9)		(2.10)
	(2.11)					(2.12)
		(2.13)

Формулы, выражающие операции векторного анализа в криволинейных ортогональных координатах, имеют следующий вид:

	(2.14)
	(2.15)
	(2.16)

Применение оператора Лапласа к скалярной функции дает следующий результат:

(2.17)

Формулы (2.14) - (2.17) легко конкретизируются в сферических и цилиндрических координатах при помощи данных из таблицы 2.2.