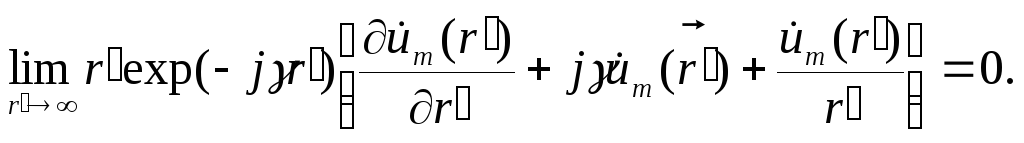7.2. Условие излучения
Остается выяснить характер решений, для которых получены представления (7.6), (7.8), и уточнить требования, которым они должны удовлетворять.
|
|
|
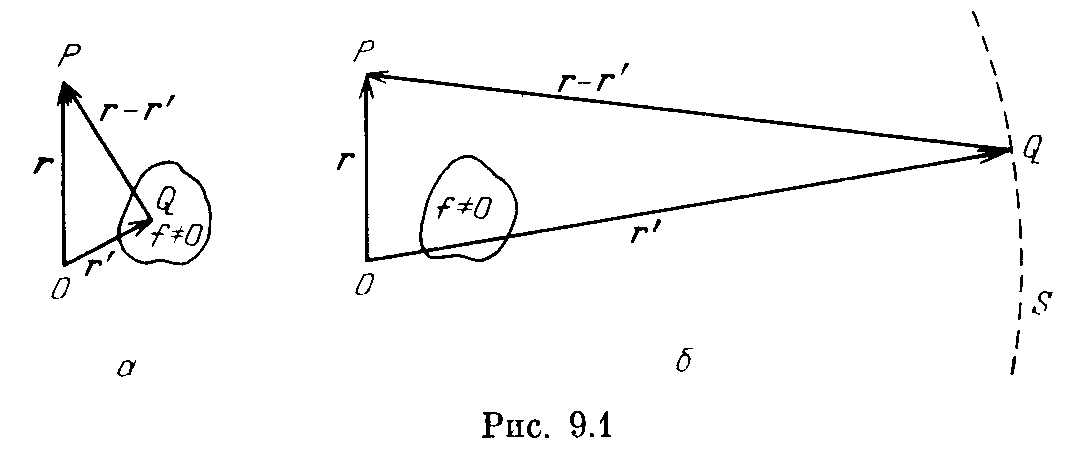
Рис. 7.1. Схема решений уравнений Гельмгольца |
Зафиксируем точку Р(r), в которой рассматривается решение. При интегрировании в формулах (7.6) и (7.8) конец Q радиус-вектора r' пробегает область, внутри которой f ≠ 0 , т. е. локализованы источники. Иллюстрация этого случая приведена на рис. 7.1,а.
При вычислении поверхностного интеграла в формуле (7.5) точка Q находится на поверхности S (рис. 7.1,б). Будем относить поверхность S в бесконечность, считая ее сферой радиуса r'. Тогда v' = r , а поскольку при r' → ∞ исчезает различие между |r - r'| и r', то подынтегральное выражение в пределе принимает следующий вид:
|
|
Поскольку площадь поверхности сферы пропорциональна (r')2, то поверхностный интеграл в формуле (7.5) при отнесении границы S в бесконечность исчезнет, если выполняется следующее условие:
|
|
Отбрасывая несущественный общий множитель и бесконечно малый член в скобках, а также изменяя обозначение аргумента r’ → r, получаем следующее условие:
|
|
(7.9) |
Этому условию должны удовлетворять решения, определяемые по формуле (7.6). Это так называемое условие излучения Зоммерфельда.
Легко убедиться, что условию излучения (7.9) удовлетворяют только решения, имеющие при r → ∞ вид расходящихся сферических волн:
|
|
(7.10) |
Это значит, что из рассмотрения исключаются все те решения, которые нельзя интерпретировать как волны, создаваемые заданными источниками.
Чтобы записать условие, определяющее класс решений векторного уравнения Гельмгольца (7.7), представляемых формулой (7.8), надо лишь заменить в (7.9) комплексную амплитуду на комплексную амплитуду вектора. Это векторное условие излучения.
Как видно, решения (7.6) и (7.8) по своему характеру выражают расходящиеся волны, т. е. волновой процесс, возбуждаемый в области источника (где f ≠ 0), который, запаздывая, распространяется в пространстве. Такой характер имеет уже функция Грина (7.3). Надо иметь в виду, что при замене ехр(-jγr) на exp(jγr) формула (7.3) определяет другую функцию Грина (решение уравнения (7.2)), которая сама имеет смысл сходящейся волны и порождает такого же рода решения уравнения (7.1). Этот класс решений лишен физической содержательности.
8. Литература
Никольский, В.В. Электродинамика и распространение радиоволн / В.В. Никольский, Т.И. Никольская. М: Наука, 1989. – 544 с. – ISBN 5-02-014033-3.
Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов / И.Н. Бронштейн, К.А. Семендяев. М: Наука, 1986. – 544 с.
Петров, Б.М. Электродинамика и распространение радиоволн / Б.М. Петров. М.: Горячая линия – Телеком, 2007. – 558 с.