моделирование экосистем

51

52

строчку 1) получилось в результате действий, которые приведены в табл.9.3.

Таблица 9.3.

	Отклонение	Численности в клетках	Произведение nxyky
	высот ку	таблицы nxy
	- 5	I	- 5
	- 4	6	- 24
	- 3	I	- 3
	- 2	I	- 2
	Всего	9	- 34

Такие подсчеты делают по каждой строчке таблицы распределения, получая цифры пятого столбца (-34, -42. -27 и т.д.).

Внизу таблицы распределения, в пятой строке, подобным образом записывают суммы произведений каждого отклонения по диаметру на соответствующие численности, расположенные в клетках по столбцам таблицы. Например, число - 42 в строке 5 (внизу таблицы) получилось исходя из следующих расчетов (табл.9.4).

Таблица 9.4.

Отклонение	Численности в клетках	Произведение nxykх
диаметров кх	таблицы nxy
- 3	6	- 18
- 2	7	- 14
- 1	10	- 10
0	3	- 0
Всего	26	- 42

Данные столбца 6 получают путем перемножения цифровых значений пятого и второго столбцов, строчки 6 - путем перемножения цифр пятой и второй строчек. Суммы чисел столбца 6 и строчки 6 должны быть равны, что следует из способа образования этих сумм (в нашем примере

707).

Кроме того, должны быть равны итоги строчки 3 и столбца 5 (в нашем примере +89), строчки 5 и столбца 3 (в нашем примере -14).

Данные столбца 7 получаются путем возведения в квадрат цифровых значений пятого столбца, столбца 8 - путем деления цифровых значений седьмого столбца на численности первого. Далее подсчитывают сумму столбца 8. Аналогичным способом получают значения строчек 7, 8.

Убедившись в правильности подсчетов корреляционной таблицы и подсчитав необходимые итоговые данные столбцов и строчек, приступают к вычислению численных характеристик корреляционной таблицы.

53

Коэффициент корреляции

Коэффициент корреляции вычисляют по формуле

	r	1/1	(9.1)
		x y

где μ1/1 - первый центральный момент произведения двух статистических величин;

σ’x σ’y - неименованные средние квадратичные отклонения статистических величин х, у.

Первый центральный момент произведения двух статистических величин вычисляют по формуле

1/1 m1/1 m1xm1y

(9.2)

где m1/1 - первый начальный момент произведения двух статистических величин;

m1x, m1y - первые начальные моменты статистических величин х, y.

Первый начальный момент произведения двух статистических величин находят по формуле

m	nxykykx	(9.3)
1/1	n

где Σnxykykx - сумма произведений отклонений на численности; Σn - общая численность выборки.

Начальные моменты и среднее квадратичное отклонение определяют по формулам, которые приведены в работе 3 «Вычисление статистических показателей вариационного ряда и использованием начальных моментов по способу произведений».

Начальные моменты по диаметру х:

первый начальный момент m					nxkx								14				0,070
1x					n				200
второй начальный момент m2x				nxk2x							866						4,330
Начальные моменты по высоте y:					n				200
первый начальный момент m				nyky								89					0,445
1y					n				200
второй начальный момент m2y			nyk2y						813
																	4,065
					n				200

54

Вторые центральные моменты:

по диаметру 2x m2x m12x 4,33 0,072 4,325

по высоте 2y m2y m12y 4,065 0,4452 3,867

Первый начальный момент произведения двух статистических величин

m	nxykxky		707	3,535
1/1	n	200

Первый центральный момент произведения двух статистических величин

1/1 m1/1 m1xm1y 3,535 ( 0,07 0,445) 3,535 0,31 3,566

Среднее квадратичное отклонение по диаметру х:

неименованное x 2x 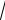4,325 2,08

именованное x i 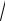2x 3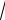4,325 6,24см

Среднее квадратичное отклонение по высоте y:

неименованное 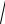y 2y 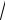3,867 1,97

именованное y i 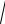2y 2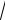3,867 3,94см

Коэффициент корреляции диаметров и высот

r	1/1		3,566		3,566	0,87
	x y		2,08 1,97
				4,098

Основная ошибка коэффициента корреляции вычисляется по формуле

	1 r2								(9.4)
	mr
			n
			1 0,87						2
	mr									0,017
	200

Таким образом, коэффициент корреляции с основной ошибкой равен r±mr=0,87±0,017.

На основании коэффициента корреляции и основной ошибки определяют его достоверность: t1 = r : mr = 0,87 : 0,017 = 52 (достоверность очень высокая, так как t1 значительно больше четырех).

Корреляционное отношение

Если высота y зависит от диаметра х, корреляционное отношение вычисляют по формуле

2	1				1		nxyky 2		m2		(9.5)
							n
y/ x			2y	n				x	1y

где μ2y - второй центральный момент по высоте μ2y=3,867;

55

Σnобщая численность выборки, Σn= 200;

nxyky 2 - итоговые данные столбца 8 (см. табл.9.2) равны 668,0; nx

m1y - первый начальный момент по высоте m1y=0,455.

Подставив цифровые значения в формулу (9.5), получим

	2	1		1		2	0,809;
								y/ x	0,809 0,90
	y/ x				668,0 0,445
		3,867		200

Основная ошибка корреляционного отношения вычисляется по

	1 2				1 0,90			2
формуле m									0,013
					200
		n

Таким образом, корреляционное отношение с основной ошибкой равно η±mη=0,90±0,013. Величина его достоверна, так как показатель достоверности t1 =0,90 : 0,013 = 69. что значительно больше четырех.

Коэффициент (индекс) детерминации

Коэффициент детерминации показывает долю изменений зависимой переменной y в соответствии с изменением независимой переменной х. Он получается путем возведения в квадрат коэффициента корреляции (при линейной зависимости) или корреляционного отношения (при криволинейной форме связи). В нашем примере корреляционное отношение η=0,90. Коэффициент детерминации Д=η2=0,902=0,81. Значение коэффициента Д означает, что у 81% деревьев высота изменяется в зависимости от диаметра, у остальных 19% деревьев изменение высот обусловлено другими причинами.

	Мера линейности
	Меру линейности вычисляют по формуле
	2 r2					(9.6)
	Для нашего случая мера линейности 0,902 0,872					0,05
	Основную ошибку меры линейности приближенно можно опреде-
	лить по формуле
	m					(9.7)
			n

где Σnсумма численностей.

56

Основная ошибка меры линейности изучаемой совокупности

m 0,05 0,00025 0,0158

200

Чтобы судить о линейности изучаемой связи, находят отношение меры линейности к ее основной ошибке. Если это отношение больше трех, то с вероятностью, близкой к единице, можно утверждать, что корреляция криволинейная. При значениях отношения меры линейности к ее основной ошибке меньше трех вероятность правильности вывода о криволинейности понижается. Это можно видеть из данных табл.9.5.

Таблица 9.5. Оценка достоверности криволинейности

Отношение φ : mξ	1,0	1,65	1,96	2,58	3,0	3,29
Вероятность правильности	0,68	0,90	0,95	0,99	0,997	0,999
вывода о криволинейности

В менее ответственных исследованиях границей прямолинейной и криволинейной связей можно принять отношение ξ : mξ=2, когда вероятность правильности о криволинейности составляет 0,95 (в 95 испытаниях из 100 вывод о криволинейности зависимости подтвердится), что бывает иногда достаточным. Чем меньше величина меры линейности, тем более точные результаты дает линейное уравнение.

Для нашего примера находим отношение ξ : mξ=0,05 : 0,0158 = 3,2. Следовательно, связь диаметра с высотой выражается некоторой

кривой линией. Вероятность правильности вывода о криволинейности очень высокая, близкая к единице. Линейность не доказана, линейное корреляционное уравнение составлять нельзя. Отметим, что мера линейности и критерий t=ξ : mξ не дают исчерпывающего ответа о выборе уравнения, позволяют лишь с определенной степенью вероятности судить о форме регрессии (прямолинейная она или криволинейная). Указание на криволинейный характер регрессии обязывает вести поиск вида уравнения среди различных функций, характеризующих наиболее точно данную криволинейную зависимость.

Показатель криволинейности

Показатель криволинейности определяется по формуле

Kp	2	r	2	(9.8)
	1 r2

57

При Кр=0 имеем строго прямолинейную зависимость двух признаков. При Кр=1 криволинейный характер связи достигает максимального предела.

Для нашего случая криволинейность равна

Kp 2 r2 1 r2

Линейное корреляционное уравнение

Если связь между двумя статистическими величинами линейная (графически выражается прямой линией), составляется корреляционное уравнение

		~	y		(9.9)
		y My r		(x Mx )
	~		x
где		- вероятное значение зависимого признака;
	y
	Мy, Мx - средние значения статистических величин y				и x;
	r - коэффициент корреляции;

σy, σx - средние квадратичные отклонения двух статистических величин (именованное, то есть с учетом величины интервала);

x - независимый признак.

В формулу (9.9) все показатели подставляются в тех единицах измерения, в которых они определяются. Действия производят над их абсолютными величинами, без учета единиц измерения. Ответ получают в единицах измерения зависимой величины y.

В формуле (9.9) выражение r y R есть коэффициент регрессии.

x

Коэффициент регрессии показывает, на сколько единиц изменится зависимый признак y, если независимый признак х изменится на единицу.

Для корреляционного уравнения определяется основная ошибка

my y	1 r	2	(9.10)
~

Основная ошибка корреляционного уравнения показывает величину ошибки, которую мы делаем, определяя на основании корреляционного уравнения вероятное среднее значение зависимого признака у, исходя из показателей независимого признака х.

58

9.2. Вычисление коэффициента корреляции и корреляционного отношения малой выборки

Для характеристики тесноты связи двух взаимосвязанных статистических величин малой выборки обычно вычисляют коэффициент корреляции и реже корреляционное отношение.

Исходными данными для данной работы являются диаметры и высоты двадцати деревьев, взятых из выборочной совокупности (200 деревьев) методом случайного отбора (каждое десятое). В примере из табл.1.1 берут диаметр и высоту каждого десятого дерева.

Для вычисления коэффициента корреляции диаметры и вы-

соты двадцати деревьев записывают в табл.9.6 (rp.2,3), вычисляют средние значения диаметра и высоты:

	средний диаметр Mx		xj						454,5		22,7см
			n					20
	средняя высота My	yj				428,1
										21,4см
		n						20

Таблица 9.6. Вычисление коэффициента корреляции для малой выборки

	№ п/п	Признаки			Центральные отклонения
		xj	yj	xj-Mx=α	yj-My=β	αβ	α2	β2
	1	2	3	4	5	6	7	8
	1	15,0	15,1	-7,7	-6,3	48,51	59,29	39,69
	2	19,5	21,0	-3,2	-0,4	1,28	10,24	0,16
	3	15,0	16,0	-7,7	-5,4	41,58	59,29	29,16
	4	18,0	17,4	-4,7	-4,0	18,80	22,09	16,00
	5	19,5	21,7	-3,2	0,3	-0,96	10,24	0,09
	6	23,5	23,0	0,8	1,6	1,28	0,64	2,56
	7	36,0	29,5	13,3	8,1	107,73	176,89	65,61
	8	19,0	17,8	-3,7	-3,6	13,32	13,69	12,96
	9	21,5	22,4	-1,2	1,0	-1,20	1,44	1,00
	10	22,0	23,8	-0,7	2,4	-1,68	0,49	5,76
	11	32,0	25,0	9,3	3,6	33,48	86,49	12,96
	12	26,0	22,7	3,3	1,3	4,29	10,89	1,69
	13	18,0	16,0	-4,7	-5,4	25,38	22,09	29,16
	14	22,5	23,6	-0,2	2,2	-0,44	0,04	4,84
	15	21,0	22,5	-1,7	1,1	-1,87	2,89	1,21
	16	23,5	22,6	0,8	1,2	0,96	0,64	1,44
	17	36,0	26,5	13,3	5,1	67,83	176,89	26,01
	18	15,5	16,0	-7,2	-5,4	38,88	51,84	29,16
	19	32,0	26,0	9,3	4,6	42,78	86,49	21,16
	20	19,0	19,5	-3,7	-1,9	7,03	13,69	3,61
	Всего	454,5	428,1	+0,5	+0,1	446,89	806,25	304,23

59

Далее находят центральные отклонения по диаметру и высоте (гр.4,5), то есть разность между вариантами и средним значением признака. Сумма центральных отклонений должна равняться нулю. Но при округлении среднего значения до десятых она может оказаться больше или меньше нуля. Величина этой невязки не должна превышать ±0,5. В графе 6 вычисляют произведение центральных отклонений, а в графах 7, 8 соответственно квадраты центральных отклонений по диаметру и высоте.

Коэффициент корреляции малой выборки вычисляется по формуле

r (9.11)

2 2

где α - центральное отклонение по диаметру; β - центральное отклонение по высоте.

Подставляя цифровые значения в формулу (9.11), получим коэффициент корреляции:

r		446,89			446,89	0,90
		806,25 304,23	495,2

Основная ошибка коэффициента корреляции малой выборки

mr 1 r2 1 0,902 0,042

n 20

Таким образом, коэффициент корреляции с основной ошибкой равен r±mr=0,90±0,042. Несмотря на небольшое количество единиц выборки, коэффициент корреляции оказался достоверным, так как показатель достоверности больше четырех:

	t1		r		0,90	21
			mr		0,042

Поэтому можно считать доказанным, что между диаметрами и высотами существует высокая связь.

Для вычисления корреляционного отношения малой выборки исходными данными возьмем 20 соотношений диаметров и высот (см.табл.9.6). Независимый признак х в нашем примере является диаметр, зависимый y – высота деревьев. Сгруппируем 20 деревьев по четырехсантиметровым ступеням толщины и поместим их в табл.9.7.

В скобках табл.9.7 приведены предельные значения диаметров ступеней толщины. Например, ступень 16 см имеет предельные диаметры 1417,9 см, ступень 20, соответственно, 18-21,9 и т.д.

Для вычисления корреляционного отношения определяют среднюю высоту всей выборки H=428,1 : 20 = 21,4 и условную среднюю высоту для

60

каждой ступени толщины в отдельности. Например, для ступени толщины 16 см условная средняя высота

hусл 15,1 16,0 16,0 47,1 15,7см 3 3

Таблица 9.7. Вычисление корреляционного отношения для малой выборки

	Ступени	Высота	Средняя высота, м			Отклонения
			ступени	всей вы-
	толщины	дерева h,			α=H-h	α2	Δ=h-hусл	2
			толщины	борки H
	d, см	м	hусл
	16	15,1			6,3	39,69	-0,6	0,36
	(14-17,9)	16,0	15,7		5,4	29,16	0,3	0,09
		16,0			5,4	29,16	0,3	0,09
	20	21,0			0,4	0,16	1,2	1,44
	(18-21,9)	17,4			4,0	16,00	-2,4	5,76
		21,7			-0,3	0,09	1,9	3,61
		17,8	19,8		3,6	12,96	-2,0	4,00
		22,4			-1,0	1,00	2,6	6,76
		16,0			5,4	29,16	-3,8	14,44
		22,5		21,4	-1,1	1,21	2,7	7,29
		19,5			1,9	3,61	-0,3	0,09
	24	23,0			-1,6	2,56	-0,2	0,04
	(22-25,9)	23,8	23,2		-2,4	5,76	0,6	0,36
		23,6			-2,2	4,84	0,4	0,16
		22,6			-1,2	1,44	-0,6	0,36
	28	22,7	22,7		-1,3	1,69	0	0
	(26-29,9)
	32	25,0	25,5		-3,6	12,96	-0,5	0,25
	(30-33,9)	26,0			-4,6	21,16	0,5	0,25
	36	29,5	28,0		-8,1	65,61	1,5	2,25
	(34-37,9)	26,5			-5,1	26,01	-1,5	2,25
	Всего	428,1	-	-	-0,1	304,23	-	49,85

Затем определяют центральные отклонения по высоте, то есть находят разность между средней высотой всей совокупности деревьев (20 штук) и высотой каждого дерева, например:

первое центральное отклонение	α1 = 21,4 – 15,1 = 6,3
второе центральное отклонение	α1 = 21,4 – 16,0 = 5,4

Далее вычисляют отклонения высот каждого дерева от среднего значения высоты данной ступени толщины (условной средней высоты ступени толщины). Например:

для ступени толщины 16 отклонения высот равны

1 = 15,1 – 15,7 = - 0,6;

2 = 16,0 - 15,7 = 0,3;

3 = 16,0 - 15,7 = 0,3;

для ступени толщины 20 отклонения высот равны