моделирование экосистем

71

вать распределение деревьев ели по диаметру и высоте (табл.1.7), на основании которой вычисляются средние высоты по ступеням толщины, используя формулу

H

h1n1 h2n2 h3п3

hknk

(11.11)

n1 n2 n3 nk

где

Н – условная высота по ступеням толщины;

h1,h2,h3 – высоты (среднее значение интервала по высоте в

корреляционной таблице);

n1,n2,n3 – численности при данном диаметре для различных высот.

Например, для диаметра 10 см

H

10 1 12 6 14 1 16 1

112

12,5м;

1 6 1 1

9

для диаметра 13 см

H

10 2 12 1 14 4 16 5 18 6

276

15,3м

18

2 1 4 5 6

Таким способом вычисляют высоты всех диаметров. Для нашего примера условные средние высоты по ступеням толщины, вычисленные по формуле (11.11), приведены в табл.11.1.

Таблица 11.1. Опытные средние высоты по ступеням толщины

	Диаметры, см	10	13	16	19	22	25	28	31	34	37	40
	Опытные средние	12,5	15,3	17,5	19,9	21,6	23,2	24,0	26,1	24,0	28,0	28,0
	высоты,м

Опытные средние высоты по ступеням толщины необходимо выравнить, используя уравнения (11.2), (11.5), (11.6) и др., а затем по способу наименьших квадратов подобрать наиболее соответствующее данному случаю. В настоящее время решение и выбор математических моделей производится на ЭВМ по специальным программам [13,14]. Однако, чтобы показать методику выбора оптимального математического уравнения сделаем вычисление уравнения параболы первого (11.1) и второго (11.2) порядка. При этом необходимо отметить, что соотношение диаметров и высот в спелом лесу нельзя выражать уравнением прямой.

Вычисление уравнения прямой y=a+bx

Сначала составляют два нормальных уравнения. Для нахождения первого нормального уравнения все члены уравнения прямой умножают на коэффициент при а, т.е. на единицу, и суммируют. Для нахождения

72

второго нормального уравнения все члены уравнения прямой умножают на коэффициент при b, т.е. на х, и суммируют.

Таким образом, имеем два нормальных уравнения прямой

y an b x
			(11.12)
	2
xy a x b x

где n – число условных средних высот (в нашем примере 11).

В соответствии с нормальными уравнениями составляют табл.11.2, где вычисляют необходимые суммы для составления уравнений.

Таблица 11.2. Вычисление уравнения прямой y=a+bx

Диаметр х,	Высота y, м	х2	xy	Высота по уравнению	~	2
				~	(y y)
см				(11.13) y,м
1	2	3	4	5	6
10	12,5	100	125,0	14,4	2,89
13	15,3	169	198,9	15,9	0,36
16	17,5	256	280,0	17,4	0,01
19	19,9	361	378,1	18,9	1,00
22	21,6	484	475,2	20,4	1,44
25	23,2	625	580,0	21,9	1,69
28	24,0	784	672,0	23,3	0,49
31	26,1	961	809,1	24,8	1,69
34	24,0	1156	816,0	26,3	5,29
37	28,0	1369	1036,0	27,7	0,09
40	28,0	1600	1120,0	29,2	1,44
275	240,1	7865	6490,3	-	16,39

Используя итоговые данные табл.11.2, в соответствии с нормальными уравнениями (11.12) можно записать:

240,1 11a 275b

6490,3 275a 7865b

Разделим каждое из уравнений на свой коэффициент при а, т.е. первое уравнение на 11, а второе – на 275. Тогда получим два новых уравнения:

21,827 a 25,000b

23,601 a 28,600b

Вычитая из второго уравнения системы первое, освобождаемся от коэффициента а и находим коэффициент b.

_23,601 = а + 28,600 b 21,827 = a + 25,000 b

1,774 =

3,600 b

b 1,774 0,493

3,600

73

Подставив значение коэффициента b=0,493 в исходное уравнение, получим коэффициент а.

21,827	= а	+ 25b
21,827	= а	+ 25 · 0,493
а = 21,827		– 12,325 = 9,502

Таким образом, уравнение прямой имеет вид:

~	(11.13)
y 9,502 0,493х

В уравнение (11.13) подставляют диаметры х, получают выравненные высоты по ступеням толщины, которые записывают в пятую графу, а квадраты отклонений опытных средних высот от вычисленных в

шестую графу табл.11.2.							коэффициентом			регрессии,
	Величина b=0,493	называется
который показывает, на сколько изменится зависимый признак										у (высота),
если независимый х (диаметр) изменится на единицу, т.е. на 1 см.
	Коэффициент а=9,502 означает уровень регрессии, ее подъем от на-
чала координат по оси ординат.
	Точность уравнения оценивают по основной ошибке, вычисляемой
по формуле
				~	2
	my			y y					(11.14)
				n e
	~ 2
где
	y y - сумма квадратов отклонений между опытными (фактиче-
	скими) у и вычисленными по уравнению							~
									увысотами;
	n – количество точек линии регрессии, по которым вычислялось
	уравнение (в нашем примере 11);
	е – количество коэффициентов уравнения.
	При выравнивании	опытных			данных				по уравнению прямой

~ 2	16,39(табл.11.2), количество коэффициентов уравнения е=2. Ос-
y y
новная ошибка уравнения (11.13) равна
			~ 2
	my		y y				16,39			1,82	1,35м
			n e
						11 2

Ошибку уравнения my называют также стандартным отклонением или средней квадратичной ошибкой уравнения. Ошибка уравнения показывает среднюю квадратичную разность отдельных опытных значений от линии регрессии. При большом количестве отклонений опытных данных от вычисленных их распределение подчиняется нормальному закону: 68% всех отклонений не выйдет за пределы однократного значения ±my, 95% будет находится в пределах ±2my и 99,7% - в пределах ±3my.

74

Вычисление уравнения параболы второго порядка y=a+bx+cx2

Система нормальных уравнений для параболы второго порядка, которую надо решить, имеет вид:

y an b x c x2
xy a x b x2 c x3								(11.15)
x	2	y a x	2	b x	3	c x	4

В целях решения системы нормальных уравнений необходимо подготовить табл.11.3 для вычисления цифровых показателей, входящих в систему уравнений (11.15).

Таблица 11.3.Вычисление уравнения параболы второго порядка y=a+bx+cx2

Диаметр	Высота	х	2	x	3	x	4	xy	2	y	Высота по	~	2
									x		уравнению	(y y)
х, см	y, м
											~
											(11.17) y,м
1	2	3		4		5		6	7		8	9
10	12,5	100		1000		10000		125,0	1250,0		13,8	1,69
13	15,3	169		2197		28561		198,9	2587,7		15,6	0,09
16	17,5	256		4096		65536		280,0	4480,0		17,4	0,01
19	19,9	361		6859		130321		378,1	7183,9		19,1	0,64
22	21,6	484		10648		234256		475,2	10454,4		20,7	0,01
25	23,2	625		15625		390625		580,0	14500,0		22,3	0,81
28	24,0	784		21952		614656		672,0	18816,0		23,7	0,09
31	26,1	961		29791		923521		809,1	25082,1		25,0	1,21
34	24,0	1156		39304		1336336		816,0	27744,0		26,3	5,29
37	28,0	1369		50653		1874161		1036,0	38322,0		27,5	0,25
40	28,0	1600		64000		2560000		1120,0	44800,0		28,5	0,25
275	240,1	7865		246125		8267973		6490,3	195228,1		-	10,34

Для нашего примера получится следующая система нормальных уравнений:

240,1 11a 275b 7865c
6490,3 275a 7865b 246125c

195228,1 7865a 246125b 8267973c

Разделим каждое уравнение на совй коэффициент при а, т.е. первое на 11, второе на 275 и третье на 7865. Тогда получим три новых уравнения (исходная система уравнений):

21,827 a 25b 715c
23,601 a 28,6b 895c

24,822 a 31,294b 1051,23c

75

Из третьего уравнения системы последовательно вычтем первое и второе уравнения:

_24,822 = а + 31,29 b + 1051,23 c 21,827 = a + 25,00 b + 715,00 c 2,995 = 6,29 b + 336,23 c

_24,822 = а + 31,294 b + 1051,23 c 23,601 = a + 28,600 b + 895,00 c 1,221 = 2,694 b + 156,23 c

Получим уравнение с двумя неизвестными, которые надо решить относительно с, b :

2,995 6,296b 336,23c

(11.16)

1,221 2,694b 156,23c

Разделим каждое уравнение (11.16) на коэффициент при b , т.е. первое на 6,296, а второе на 2,694. Тогда получим новую систему уравнений:

0,4758 b 53,403c

0,4532 b 57,992c

Чтобы освободится от коэффициента b , найдем разность уравне-

ний:

_0,4532 = b + 57,992 c 0,4758 = b + 53,403 c

-0,0226 =

4,589 c

с 0,0226 0,00492 4,589

Для нахождения коэффициента b подставим значение с=-0,00492 в урав-

нение 0,4758=b+53,403с. Тогда найдем, что b=0,7385.

Цифровые значения коэффициентов (b=0,7385 и с=-0,00492) подставим в уравнение 21,827 = а + 25b + 715с.

Тогда найдем, что а=6,882.

Для проверки правильности вычисления коэффициентов их значения подставляют в исходную систему уравнений. Лишь после проверки коэффициентов их цифровые значения подставляют в исходное уравнение, получая конкретное уравнение для данного случая.

		~	2	(11.17)
		y 6,882 0,7385x 0,00492x
Подставляя в уравнение (11.17) диаметры				х, определяют выравнен-
ные высоты	~	, которые заносят в восьмую графу (табл.11.3). Например,
	y

при диаметре х=10 см высота по уравнению (11.7)

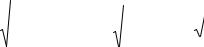
76

~

2

13,775 13,8см.

y 6,882 0,7385 10 0,00492 10

В девятой графе вычисляют квадраты разностей между опытными и

вычисленными по уравнению

высотами, а затем подсчитывают сумму

квадратов отклонений

~ 2

10,34.

y y

Основная ошибка уравнения по формуле (11.14) равна

~

2

my

y y

10,34

1,29

1,14м

n e

11 3

Выбор оптимального уравнения

В заключение необходимо сделать вывод о том, какое уравнение лучше отражает связь диаметров и высот исследуемой совокупности. Для этого используют метод наименьших квадратов, в результате применения которого для нашего примера получены следующие результаты

(табл.11.4).

Данные табл.11.4. показывают, что для нашего примера лучшие результаты выравнивания высот по ступеням толщины дает уравнение параболы второго порядка y=a+bx+cx2.

Таблица 10.4. Основные ошибки уравнений

Вид уравнения	Сумма квадратов отклонений	Ошибка уравнения
Уравнения прямой y=9,502+0,493х	16,39	1,35
Уравнение параболы второго по-	10,34	1,14
рядка у=6,882+0,7385х-0,00492х2

Оптимальное уравнение, характеризующее зависимость высоты деревьев от диаметра исследуемой выборочной совокупности записывают с основной ошибкой

h 6,88 0,739d 0,00492d2 ;mh 1,14

(11.18)

где h – высота дерева, м;

d – диаметр дерева на высоте 1,3 м от шейки корня, см; mh- основная ошибка уравнения, м.

Для наглядности опытные и выравненные по оптимальному уравнению (11.18) высоты изображают графически (рис.11.1).

77

12.ДИСПЕРСИОННЫЙ АНАЛИЗ

12.1.Основные понятия и задачи дисперсионного анализа

Основная задача дисперсионного анализа заключается в изучении статистического влияния одного или нескольких факторов на результативный признак. Такое влияние можно установить на основе эксперимента, в результате которого получают данные об изучаемом явлении с определенной повторностью. При постановке опыта, наряду с многочисленными факторам, приводящими к разнообразию подопытных объектов, действует и такой фактор, изучение которого является основной задачей исследования.

Исследователь по своему усмотрению может регулировать степень воздействия основного фактора на результативный признак. Различное воздействие отразится на варьировании объектов. Анализируя такие материалы, Р.А.Фишер пришел к плодотворной идее подразделения общего варьирования на части, с глубоким анализом показателей разнообразия [10,23]. Для этого Р.А.Фишер пользовался суммой квадратов отклонений и назвал ее дисперсией. Конечные результаты дисперсионного анализа получают на основе дисперсий. Это и определило название метода - дисперсионный анализ.

Дисперсия происходит от латинского слова dispersus, что означает рассеяние. Дисперсией называется сумма квадратов отклонений отдельных вариант от среднего значения. Дисперсия, как и среднее квадратичное отклонение, характеризует степень разнообразия отдельных единиц наблюдения в пределах однородной совокупности. Основные статистические показатели, их содержание и способы вычисления изложены в предыдущих разделах.

При дисперсионном анализе выделяют результативный признак и действующие факторы. Результативный признак Y - это такое качество или свойство объектов, которое образуется в результате влияния организованных Х и неорганизованных Z (всех остальных) факторов в данном исследовании.

Результативными признаками в лесном хозяйстве могут быть: высота, диаметр и объем стволов; запас древесины на единице площади; прирост древесины ствола и запаса древостоя; высота сеянцев в питомнике; количество подроста в лесу; урожай семян и др.

Действующий фактор - это любое влияние (воздействие или состояние), которое отражается на результативном признаке. Факторами могут быть: различная интенсивность изреживания древостоя, осушительная ме-

78

лиорация, удобрения, температура воздуха, возраст деревьев или древостоев, тип возрастной структуры и др.

Факторы при дисперсионном анализе формируют в градации, представляющие собой различные степени их воздействия или состояния объектов изучения (доза удобрения; возраст деревьев; температура; величина признака, принимаемого за аргумент и др.). При обработке опытных данных необходимо обязательно учитывать градации факторов. При различной степени воздействия факторов в эксперименте организуют отдельные группы опыта. В результате формируются градации комплекса.

Каждая градация комплекса соответствует одной градации фактора и включает те объекты, которые подвергались одной степени воздействия фактора или находились в одном из изучаемых состояний. Подбор объектов в градации производится по принципу случайной выборки, то есть рендомизированно. При постоянной степени воздействия регулируемого фактора возможно наличие повторности результативного признака в эксперименте. Например, при одной и той же дозе удобрения спелых сосновых лесов (200 кг/га) прирост составил 6,8; 6,1; 7,4 м3 [29].

Для обработки и анализа экспериментальных данных формируется дисперсионный комплекс, в котором учитываются варианты опыта и их повторности. Дисперсионный комплекс представлен таблицей, в которой исходные данные объединены в градации для изучения эффективности действия организованных факторов на результативный признак. При этом по каждой градации и в целом по всему комплексу вычисляют средние значения признака.

Различают однофакторные, двухфакторные и многофакторные комплексы. Однофакторные комплексы применяются для оценки силы и достоверности влияния одного фактора, требующего опытной проверки. Двухфакторные комплексы используются для оценки и сопоставления силы и достоверности влияния двух одновременно изучаемых факторов, многофакторные - трех и более факторов. Когда во всех градациях имеется одинаковое число единиц, дисперсионный комплекс называют равномерным при неодинаковом - неравномерным.

При дисперсионном анализе выделяют факториальные, случайные и общие факторы, которые вызывают изменчивость результативного признака. В соответствии с этим общее варьирование делят на две части. Одна часть отражает изменчивость, вызываемую основным (изучаемым) фактором, а другая - изменчивость, вызываемую случайными (неорганизованными) причинами. Дисперсии факториального Dф и случайного Dс признаков в сумме дают общую дисперсию:

79

DO DФ DС

(12.1)

Одна из главных задач дисперсионного анализа заключается в установлении статистического влияния регулируемых факторов на результативный изучаемый признак путем разложения общей дисперсии на составные части. Дисперсионный анализ позволяет установить долю участия, силу влияния и достоверность действия изучаемых факторов в эксперименте.

12.2.Дисперсионный анализ однофакторного комплекса

12.2.1.Опытные материалы

Технические приемы дисперсионного анализа разберем на конкретном примере. В разновозрастном еловом древостое методом случайного отбора выбраны 22 дерева различного возраста и измерена их высота. Действующий фактор - возраст, результативный признан - высота деревьев. Заметим, что в однофакторных комплексах фактором может быть любое воздействие на результативный признак (условия роста, химические или биологические препараты, те или иные признаки растений и др.).

Для нашего примера в каждой градации возраста взято от 4 до 7 деревьев. Все они произрастают на одном участке ельника черничного в средней подзоне тайги. По полученным данным составлена табл.12.1.

Таблица 12.1. Опытные данные

Возраст дерева, лет	Высота дерева, м
80	14;15;10;8;16
120	23;21;20;14;17;12;19
160	24;20;17;23;16;23
200	22;19;24;21

Задача исследования заключается в установлении степени и достоверности влияния возраста деревьев на высоту в разновозрастном лесу. Необходимо также определить градацию возраста, начиная с которой увеличение высоты деревьев не имеет большого хозяйственного значения.

12.2.2. Построение дисперсионного комплекса

Опытные данные по градациям факториального признака (возраста) записываются в табл.12.2.

Далее вычисляются средние значения по градациям и по всему комплексу. Среднее значение по комплексу определяется по формуле

	M0		y	(12.2)
			N

80

где ΣΣy – сумма всех вариантов в комплексе;

N – общее число единиц наблюдения (повторений) в комплексе.

В нашем примере М0=396:22=18,0. Средние значения по градациям вычисляются по формуле

	MГ	y	(12.3)
		n

где Σy – сумма вариант по градациям;

n – число единиц наблюдения (повторений) результативного признака по градациям.

Таблица 12.2. Однофакторный дисперсионный комплекс

Градация фак-	Результативный при-	Число повто-	Сумма высот	Среднее значение
тора (возрас-		рений по гра-		по градациям МГ,
та), лет	знак (высота) у, м	дации n	Σу, м	м
80	14;15;10;8;16	5	63	12,6
120	23;21;20;14;17;12;19	7	126	18,0
160	24;20;17;23;16;23	6	123	20,5
200	22;19;22;21	4	84	21,0
Итого	-	22	396	-

Решение дисперсионного комплекса начинается с анализа групповых средних значений. В комплексе средние значения по градациям указывают на заметное влияние изучаемого фактора (возраста) на результативный признак – высоту деревьев. Повышение градации возраста деревьев сопровождается увеличением групповых средних высот. При меньшем значении возраста увеличение высоты идет быстрее, а при большем возрасте – медленнее.

После рассмотрения ряда групповых средних значений производится расчет дисперсий комплекса.

12.2.3. Вычисление дисперсий комплекса

В однофакторном дисперсионном комплексе определяются факториальная, случайная и общая дисперсии.

Факториальная (межгрупповая) дисперсия вычисляется как сумма квадратов центральных отклонений групповых средних от общей средней по всему комплексу (табл.12.3).

Факториальная дисперсия

Dф МГ М0 2n 2n

(12.4)

где α – центральное отклонение.