Аналитическая геометрия. Поверхности второго порядка

89

Это свойство гиперболического параболоида также используется в строительных конструкциях: из прямолинейных металлических элементов создается каркас кровли в форме гиперболического параболоида. Такая поверхность, благодаря своей кривизне, обладает собственной жесткостью, тогда как жесткость кровли традиционной формы - в виде совокупности плоских участков – обеспечивается поддерживающими конструкциями (стропилами) и требует дополнительного расхода материалов.

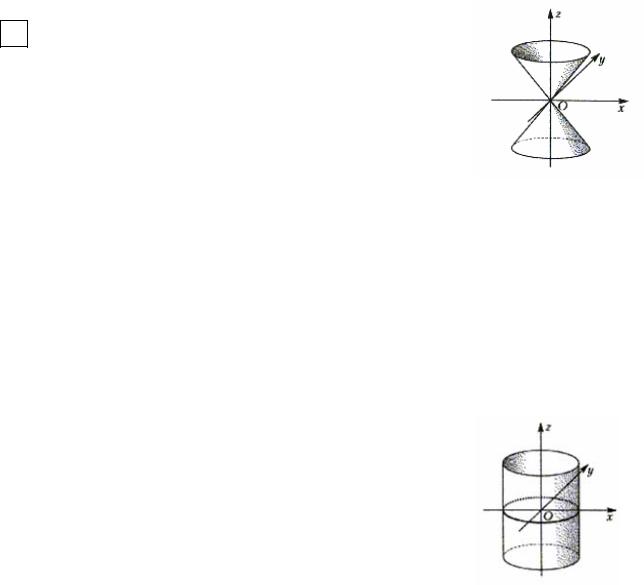
7.5.6. Конус

ОЭллиптическим конусом называется поверхность с каноническим уравнением

	x2	+	y2	−	z2	= 0 .
	a2		b2		c2

Сечения плоскостями z = const - эллипсы, размеры которых возрастают по мере удаления от начала координат; сечения плоскостями, проходящими через ось Oz , - скрещивающиеся прямые.

Цилиндры

В выбранной системе координат образующие цилиндров параллельны оси Oz и уравнения не содержат координаты z. Это свойство сохраняется и для уравнения общего вида (5): если уравнение не содержит какой-либо переменной, то определяемая им поверхность – цилиндр, образующие которого параллельны соответствующей оси.

7.5.7. Эллиптический цилиндр

О	Эллиптический цилиндр задается каноническим
	уравнением:	x2	+	y2	=1.
		a2		b2

Осью цилиндра является координатная ось Oz , поперечные сечения – эллипсы. Плоскости Oxz и Oyz являются

плоскостями зеркальной симметрии поверхности.

90						Лекция 7
	7.5.8. Гиперболический цилиндр
		Гиперболический цилиндр задается каноническим
	О
		уравнением:	x2	−	y2	=1.
			a2		b2
	Осью цилиндра является координатная ось Oz , попереч-
	ные сечения – гиперболы. Плоскости Oxz и Oyz являют-
	ся плоскостями зеркальной симметрии поверхности.
	7.5.9. Параболический цилиндр
		Параболический цилиндр задается каноническим
	О
		уравнением: y2 = 2 px, p > 0 .

Плоскость Oxz является плоскостью зеркальной симметрии поверхности.

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

различные виды поверхностей, их свойства;

канонические уравнения поверхностей второго порядка, уметь исследовать их методом сечений.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Лекции 8 - 9 ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И

МАТЕМАТИЧЕСКОЙ ЛОГИКИ. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Влекциях 8 – 9 излагаются необходимые элементы теории множеств, рассматриваются наиболее часто встречающиеся числовые множества и их свойства. Вводится понятие числовой последовательности и ее предела, рассмотрены специальные виды последовательностей (бесконечно малые, бесконечно большие, монотонные) и их свойства.

8.1.Элементы теории множеств и математической логики

8.2.Числовые множества

8.3.Числовые промежутки

8.4.Ограниченные множества

8.5.Числовые последовательности

8.6.Свойства ограниченных последовательностей

9.1.Предел числовой последовательности

9.2.Бесконечно большие и бесконечно малые последовательности

9.3.Свойства бесконечно малых последовательностей

9.4.Свойства сходящихся последовательностей

9.5.Монотонные последовательности

9.6.Число е как предел монотонной последовательности

9.7.Предельные точки. Верхний и нижний пределы

8.1.Элементы теории множеств и математической логики

Вдальнейшем для сокращения записей будут использоваться некоторые

понятия и операции теории множеств и математической логики.

Понятие множества относится к основным понятиям математики и в силу этого его нельзя определить через какое-то более общее понятие.

ООбъекты, имеющие какой-либо общий признак и рассматриваемые как единое целое, составляют множество; сами объекты по отношению к множеству являются элементами множества.

Элементы множества, в свою очередь, также могут быть множествами. Например, учащиеся школы № N образуют множество, каждый ученик (уче-

92	Лекции 8 – 9

ница) – элемент этого множества. Это же множество можно организовать иначе: множество учащихся школы № N состоит из классов школы № N, а класс школы № N состоит из учеников (учениц) данного класса.

Множества принято обозначать заглавными латинскими буквами, элементы множеств – малыми латинскими буквами.

Множества могут быть заданы:

простым перечислением элементов (элементы заключаются в фигурные скобки): A ={1, 2, 3} ;

указанием общего признака всех элементов: X ={x : 1 < x < 2}.

Впервом примере множество состоит из 3 чисел 1, 2 и 3; во втором

примере множество состоит из бесконечного количества действительных (если не оговорено иное) чисел, удовлетворяющих условию 1 < x < 2 .

ОМножество, не содержащее элементов, называется пустым.

ОЕсли все элементы множества B являются также элементами множества

A , то B называется подмножеством множества A .

Пустое множество является подмножеством любого множества, Любое непустое множество является подмножеством самого себя (это так называемые несобственные подмножества).

О Множества A и B равны, если одновременно A - подмножество B и B - подмножество A . Равные множества состоят из одних и тех же элементов.

Рассмотрим способы сокращенной записи некоторых утверждений относительно множеств и операций над множествами:

a A

a A

A B

A B A = B

A B

пустое множество;

« a принадлежит множеству A » (« a содержится в множестве A », «множество A содержит a », «множество A включает элемент a »);

«элемент а не принадлежит множеству A »;

« B - подмножество множества A » (« A содержит B », « B содержится в A », « A включает B », « B включается в A »);

« A - подмножество множества B »;

«A равно B», «А совпадает с В»;

объединение (сумма) множеств А и В; вобъединение входят элементы, принадлежащие хотя бы одному из этих множеств;

A ∩ B пересечение (произведение) множеств А и В; в пересечение входят элементы, каждый из которых принадлежит и множеству А, и множеству B.

Элементы теории множеств и математической логики. Числовые последовательности

93

Рассмотрим способы сокращенной записи некоторых логических операций и стандартных словосочетаний (ниже малыми греческими буквами будут обозначаться некоторые высказывания (утверждения)):

α β	импликация, логическое следствие; читается «из высказыва-
	ния α следует высказывание β », «высказывание β является
	следствием высказывания α »;
α β	эквивалентность, равносильность; читается «высказывание
	α равносильно высказыванию β », «α эквивалентно β », «α
	и β равносильны»; означает, что α β и β α , т.е. выска-
	зывания α и β либо оба верны, либо оба неверны;

αотрицание высказывания α ;

дизъюнкция, логическое «или»; α β означает «α или β »;

конъюнкция, логическое «и»; α β означает «α и β »;

квантор существования, α A – читается «существует элемент a , принадлежащий множеству A»;

квантор всеобщности, α A – читается «для каждого элемента α , принадлежащего множеству A».

:читается «такой, что», «удовлетворяющий условию», «имеет место».

Кроме того, далее будут использоваться сокращенные способы записи сумм и произведений большого количества элементов:

n	n
∑a j = a1 + a2 +…+ an ,	∏a j = a1 a2 … an .
j=1	j=1

Покажем на нескольких примерах применение символической записи:

1)(x A B) ((x A) (x B)) - определение объединения;

2)(A = B) ((A B) (A B)) - определение равенства множеств;

3)(A B) ( x B : ((x B) (x A))) - определение подмножества.

8.2. Числовые множества

О	Числа	1, 2, 3,...	называются натуральными и обозначаются
	={n} ={1,2,3,...,n,...}.
О	Числа	={ 0, 1, −1,	2, −2, ... , ±n, ...}, n , образуют множество це-

лых чисел.