Аналитическая геометрия. Прямая и плоскость в пространстве	55
5.1. Основы аналитической геометрии

5.1.1. Уравнение поверхности

Аналитическая геометрия ставит своей задачей изучение геометрических объектов с помощью аналитического метода. Геометрические объекты: точка, линия, поверхность.

Точка. Задается аналитически совокупностью чисел: одного - для точки на прямой; двух - для точки на плоскости; трех - для точки в пространстве. Эти числа называются координатами.

Введем в пространстве декартову прямо-
угольную систему координат, т.е. зададим на-
G	G	G
чало координат 0, базис i	j	k , оси Ox, Oy, Oz.

О	Декартовыми координатами точки М называются декартовы коорди-
	JJJJG
	наты ее радиус–вектора OM ={ x, y, z }.
	Более сложные геометрические объекты задаются уравнениями, связы-
	вающими координаты точек, принадлежащих данному объекту. Эти
	уравнения реализуют условия принадлежности точки данному геомет-
	рическому объекту.
	Пусть задано уравнение: F (x, y, z) = 0 (*) и поверхность S. Поверхность
	S - есть геометрическое место точек, определяемое уравнением (*), если
	координаты точек поверхности S удовлетворяют уравнению (*), а коор-
	динаты любой точки, не лежащей на ней, - не удовлетворяют.

ОПоверхность, определяемая в декартовой системе координат алгебраическим уравнением n–й степени, называется алгебраической поверхно-

стью n–го порядка.

5.1.2.Уравнения линии

Ваналитической геометрии каждая линия в пространстве рассматривается как пересечение двух поверхностей и определяется заданием двух уравнений.

Если F(x, y, z)=0 и Ф(x, y, z)=0 являются уравнениями двух поверхностей

S1 и S2, пересекающихся по линии L , то линия L есть геометрическое место общих точек этих поверхностей, координаты которых удовлетворяют систе-

F (x, y, z) = 0,

ме уравнений: L :

Φ(x, y, z) = 0.

56

Лекция 5

5.2. Плоскость в пространстве

5.2.1.Плоскость как поверхность первого порядка. Общее уравнение плоскости

ТВ декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Возьмем на плоскости P произвольную точкуM0 (x0 , y0 , z0 ) . Выберем вектор n ={A, B,C}, перпендикулярный плоскости (нормальный вектор). Пусть M (x, y, z ) – произвольная точка плоскости P . Точка M

принадлежит плоскости P (записывается: M (x, y, z ) P ) тогда и только

JJJJJJG

G

JJJJJG

G

тогда, если M

M

n

=> (M

M

n) = 0 .

0

0 JJJJJG

={x − x , y

− y

, z − z

}, то

скалярное

Так как nG ={A, B,C}, M

0

M

произведение

0

0

0

G

JJJJJG

) +C(z − z

) .

(n

M

0

M ) = A(x − x ) + B( y − y

0

0

0

Уравнение плоскости, проходящей через точку M0 (x0 , y0 , z0 )

с нормаль-

ным вектором nG ={A, B,C}, имеет вид:

A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0 .

Раскрывая скобки и

обозначая

через D = −Ax0 − By0 −Cz0 , получим

уравнение первой степени (так называемое общее уравнение плоскости):

Ax + By +Cz + D = 0 .

Составим, например, уравнение плоскости, проходящей через точку M (1,1,1) перпендикулярно

к вектору nG ={2,2,3}. Искомое уравнение примет вид:

2(x −1)+ 2(y −1)+ 3(z −1)= 0 ,

2x + 2 y +3z −7 = 0 .

СЕсли два уравнения A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 определяют одну и ту же плоскость, то коэффициенты их пропорциональны:

A1 = B1 = C1 = D1 .

A2 B2 C2 D2

Аналитическая геометрия. Прямая и плоскость в пространстве

57

5.2.2. Неполные уравнения плоскостей

Если в общем уравнении плоскости отсутствуют какие-то слагаемые, то оно называется неполным.

Рассмотрим частные случаи уравнения первой степени

Ax + By +Cz + D = 0 .

D = 0: Ax + By + Cz = 0 - плоскость, проходящая через начало координат.

Эти уравнения определяют плоскости, параллельные соответственно координатным осям OX, OY, OZ, так как соответствующие компоненты нормального вектора плоскости равны нулю:

А = 0: By + Cz + D = 0	- n ║YOZ → P ║ OX;
B = 0: Ax + Cz + D = 0	- n ║XOZ → P ║ OY;
C = 0: Ax + By + D = 0	- n ║XOY → P ║ OZ.

Эти уравнения определяют плоскости, параллельные соответственно координатным плоскостям OXY, OXZ, OYZ:

A = 0, B = 0: Cz + D = 0	- n ║OZ → P ║ XOY;
A = 0, C = 0: By + D = 0	- n ║OY → P ║ XOZ;
B = 0, C = 0: Ax + D = 0	- n ║OX → P ║ YOZ.
Эти уравнения определяют координатные плоскости XOY, XOZ,YOZ:
A = 0, B = 0, D = 0: Cz = 0	- плоскость XOY;
A = 0, C = 0, D = 0: By = 0	- плоскость XOZ;
B = 0, C = 0, D = 0: Ax = 0	- плоскость YOZ.

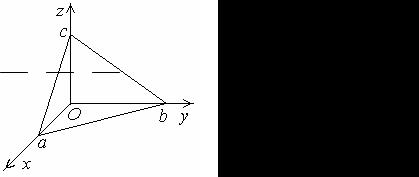
5.2.3. Уравнение плоскости «в отрезках»

Пусть плоскость не проходит через начало координат. Преобразуем общее уравнение плоскости:

Ax + By +Cz = −D, −AxD + −ByD + −CzD =1,

	x	+		y	+		z	=1.
−	D		−	D		−	D
	A			B			C

58

Лекция 5

Уравнение

x

+

y

+

z

=1 называется уравнением плоскости «в отрезках».

a

b

c

Параметры a = −D

,

b =

−D

,

c =

−D

представляют собой координаты точек

A

B

C

пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.

Пусть, например, точка лежит на оси Оx и плоскости Р, т.е. y0 = z0 = 0 .

Тогда xa0 =1, откуда x0 = a .

Пример:

Какие отрезки отсекает на осях координат плоскость

2x – 4y + 6z –12 = 0?

Приведем общее уравнение плоскости к виду уравнения «в отрезках»: 122x − 124 y + 126z =1 6x + −y3 + 2z =1.

Отрезки, отсекаемые на осях, равны a = 6 , b = −3 , c = 2 . Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy .

5.2.4. Нормальное уравнение плоскости

Пусть Р – основание перпендикуляра, опущен-

ного из начала координат на плоскость, а									M (x, y, z )
– произвольнаяJJJGточка								JJJG	={x, y, z}),
						плоскости (OM
				= p ,		nG		– единичный вектор нор-
длина вектора	OP
						0
							JJG
			nG
мали к плоскости,					=1,		n ={cosα,cos β,cosγ}.
			0					o

Проекция радиус-вектора любой точки плоско-

сти на направление, задаваемое вектором n0 – вели-

JJJG

чина постоянная, равная p: прnG0 OM = p ,

JJJJG JJJJG JJG

прnG0 OM =OM n0 = xcosα + y cos β + z cosγ .

Уравнение xcosα + y cos β + z cosγ = p задает нормальное уравнение плоскости в виде

xcosα + y cos β + z cosγ − p = 0 ,

где cosα,cos β,cosγ - направляющие косинусы нормали к плоскости, а p –

расстояние от плоскости до начала координат (длина нормали, опущенной на плоскость из начала координат).