Аналитическая геометрия. Прямая и плоскость в пространстве

63

5.3.5. Общие уравнения прямой

Рассмотрим две плоскости:

A1x + B1 y + C1z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.

Если A1 = B1 = C1 , то плоскости параллельны. В противном случае плоско-

A2 B2 C2

сти пересекаются и соответствующие уравнения определяют прямую линию пересечения плоскостей.

5.3.6. Уравнение пучка плоскостей, проходящих через прямую

Пусть прямая L задана линией пересечения двух плоскостей:

A1x + B1 y + C1z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.

Возьмем любые отличные от нуля числа α и β и составим равенство

α( A1x + B1 y +C1z + D1) + β( A2 x + B2 y +C2 z + D2 ) = 0 .

Это равенство определяет плоскость, которая проходит через прямую L. Совокупность всех плоскостей, проходящих через одну и ту же прямую, назы-

вается пучком плоскостей. Если положить λ = βα , то уравнение

A1x + B1 y +C1z + D1 + λ( A2 x + B2 y +C2 z + D2 ) = 0

определяет все плоскости пучка, кроме второй из задающих прямую.

5.3.7.Угол между двумя прямыми. Условия параллельности

иперпендикулярности двух прямых

Пусть заданы направляющие векторы прямых

L1 : aG1 ={l1,m1,n1}, L2 : aG2 ={l2 ,m2 ,n2}.										ϕ
Угол между прямыми принимается равным углу
между направляющими векторами:
cosϕ =			l1l2 + m1m2 + n1n2						L1	L2
									.
	l2	+ m2		+ n2	l2	+ m2		+ n2
	1	1		1	2	2		2

64									Лекция 5
Прямые будут параллельны, если их направляющие векторы							aG	и	aG	парал-
	l1		m1		n1		1		2
лельны, т.е.		=		=		.
	l		m
					n
	2	2		2

Прямые будут перпендикулярны, если их направляющие векторы перпендикулярны, то есть, l1l2 + m1m2 + n1n2 = 0 .

5.4. Прямая и плоскость

5.4.1. Точка пересечения прямой и плоскости

Пусть даны уравнения прямой L и плоскости P :

L : x −l x0 = y −my0 = z −nz0 ,

P : Ax + By +Cz + D = 0.

Координаты точки пересечения прямой L и плоскости P должны одновременно удовлетворять этим уравнениям. Перейдем к параметрическим уравнениям прямой:

x = x0 +lt, y = y0 + mt, z = z0 + nt .

Подставляя их в уравнение плоскости P , получим значение параметра t, рав-

ное t = − Ax0 + By0 +Cz0 + D , подстановка которого в параметрические урав-

Al + Bm +Cn

нения прямой даст координаты точки пересечения прямой и плоскости.

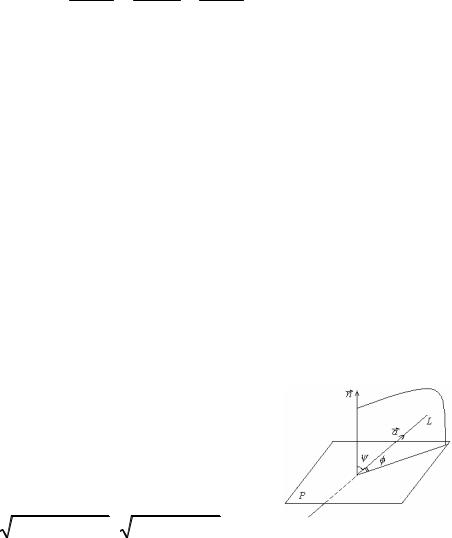
5.4.2.Угол между прямой и плоскостью. Условия параллельности

иперпендикулярности прямой и плоскости

Из рисунка видно, что если ϕ– угол между прямой и плоскостью, то

	G	G		π
	m				−ϕ = sinϕ
	cos(n, a)= cosψ = cos
				2
	sinϕ = cos(π	−ϕ) =		Al + Bm +Cn				.
			A2 + B2 +C2 l2 + m2 + n2
	2

Аналитическая геометрия. Прямая и плоскость в пространстве

65

Прямая L перпендикулярна плоскости P, если направляющий вектор пря-

мой коллинеарен нормальному вектору плоскости, т.е. Al = mB = Cn .

Прямая L параллельна плоскости P, если направляющий векторG G прямой перпендикулярен нормальному вектору плоскости, (a n) = 0, т.е.

Al + Bm +Cn = 0.

В результате изучения материала, изложенного в этой лекции, студент должен знать:

виды уравнений плоскости, назначение каждого вида, способ преобразования одного вида в другой;

виды уравнений прямой, назначение каждого вида, способ преобразования одного вида в другой;

способы решения стандартных задач, связанных с прямой и плоскостью: (угол между плоскостями, между прямыми, между прямой и плоскостью, условия параллельности и перпендикулярности этих объектов, расстояние от точки до плоскости, координаты точки пересечения прямой и плоскости).

Лекция 6 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

Лекция 6 посвящена аналитической геометрии на плоскости. Рассмотрены задачи, связанные с простейшими объектами на плоскости – точками и прямыми. Подробно анализируются кривые второго порядка: выводятся канонические уравнения кривых, исследуется их форма, обсуждаются элементы кривых. Показано, что преобразованиями координат, т.е. параллельным переносом и поворотом координатных осей общее уравнение второго порядка можно привести к каноническому виду. Заканчивается лекция рассмотрением линий в полярной системе координат и линий, заданных параметрически.

6.1.Простейшие задачи на плоскости

6.1.1.Расстояние между двумя точками

6.1.2.Деление отрезка в данном отношении

6.2.Прямая линия на плоскости

6.2.1.Общее уравнение прямой

6.2.2.Каноническое уравнение прямой

6.2.3.Уравнение прямой, проходящей через две точки

6.2.4.Уравнение прямой, проходящей через данную точку

взаданном направлении

6.2.5.Уравнение прямой в отрезках

6.2.6.Нормальное уравнение прямой

6.2.7.Расстояние от точки до прямой

6.2.8.Координаты точки пересечения двух прямых

6.2.9.Угол между двумя прямыми

6.2.10.Условие параллельности и перпендикулярности двух прямых

6.3.Кривые второго порядка

6.3.1.Эллипс

6.3.2.Окружность

6.3.3.Гипербола

6.3.4.Парабола

6.4.Преобразования координат

6.4.1.Параллельный перенос

6.4.2.Поворот координатных осей

6.4.3.Изменение начала координат и поворот осей

6.4.4.* Приведение общего уравнения кривой второго порядка к каноническому виду

6.5.* Линии в полярной системе координат 6.5.1.* Полярные координаты на плоскости

6.5.2.* Связь полярных координат с декартовыми 6.5.3.* Уравнения линий в полярной системе координат

6.6.* Параметрическое задание линий 6.6.1.* Окружность 6.6.2.* Циклоида 6.6.3.* Астроида