Аналитическая геометрия на плоскости

79

6.5.2*. Связь полярных координат с декартовыми

Совместим начало декартовой системы с полюсом полярной системы координат, а ось OX с полярной осью ρ. Найдём связь координат точки M(x,y) и M(ρ,ϕ). Она выражается следующей системой уравнений:

x = ρ cos ϕ,	ρ =	x 2 + y 2 ,
	tgϕ	= y	.
y = ρ sin ϕ,
		x
Если известны координаты точек			A(x1,y1)			и	B(x2,y2), то проекции отрезка
AB = {x2 − x1, y2 − y1}= {ρ cosϕ, ρ sinϕ},			а полярный угол отрезка по координатам его
начала и конца находится по формулам:
cosϕ = x2 − x1 , sinϕ =				y2 − y1			,
	ρ					ρ
tgϕ = y2 − y1 , ρ = (x				2	− x )2		+ ( y	2	− y )2 .
	x2 − x1					1			1

6.5.3*. Уравнения линий в полярной системе координат

Построим линию ρ = a cos ϕ, а = const>0. Координата

ρ принимает только положительные значения. При ϕ = 0 cosϕ =1, ρ = a получаем точку А(а,0).

Рассмотрим точку М(ρ,ϕ). Из уравнения линии - cosϕ = ρa ,

значит угол ОМА - прямой. С возрастанием угла ϕ от 0 до π/2 косинус этого угла убывает от 1 до 0, таким образом, ρ убывает от а до 0 в точке О(0, π/2) и радиус-вектор точки М

описывает верхнюю половину окружности. Нижняя её половина получается при изменении ϕ от 3π/2 до 2π. Этим значениям угла соответствуют положительные значения cosϕ, возрастающие от 0 до 1, что приводит к возрастанию ρ от 0 до а и геометрическому замыканию окружности.

Итак, уравнение ρ = a cosϕ задаёт окружность с центром в точке (a/2,0) и радиусом a/2. Такой же результат получается, если в уравнении линии ρ = a cosϕ перейти к декартовым координатам.

	Тогда x2 + y2 = a		x	, x2 + y2 −ax = 0, (x − a )2	+ y2	= a2	- каноническое уравнение
		x2	+ y2
				2		4
	окружности с центром в точке (a/2,0) и радиусом a/2.							p
	В полярных координатах кривые второго порядка имеют уравнения ρ =								, если
								1−e cosϕ

полюс находится в фокусе, полярная ось направлена из фокуса к ближайшей вершине (для гиперболы этим уравнением определяется только одна ветвь); р - фокальный параметр, е - эксцентриситет кривой.

80

Лекция 6

6.6*. Параметрическое задание линий

Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: - x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости. Методом исключения параметра уравнение линии приводится к уравнению в декартовых координатах, и, наоборот, линия, заданная в декартовых координатах, может быть приведена к виду кривой, заданной параметрически.

6.6.1*. Окружность

Пусть M(x,y) - текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью OX. Из треугольника ОМА:

x = R cos t,y = R sin t,

- параметрические уравнения окружности.

Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их: x2 + y 2 = R 2 (cos 2 t + sin 2 t) = R 2 . Таким образом, получено уравнение окружности в декартовых координатах.

6.6.2*. Циклоида

Обыкновенной циклоидой называется кривая, описываемая точкой круга, катящегося без скольжения по прямой линии.

Пусть OX - прямая, по которой катится круг радиуса а. Тогда МС = СК = а, где К - точка касания. За параметр t примем угол поворота МС относительно СК: t = MCK - угол качения (в радианах). Так как качение окружности происходит без скольжения, то

ОК= MK =at.

Из рисунка видно, что

x = OP = OK − PK = OK − MQ = at −a sin t = a(t −sin t), y = PM = KC −QC = a −a cos t = a(1−cos t).

Таким образом, параметрические уравнения циклоиды	x = a(t	− sin t),	где
		− cos t),
	y = a(1

− ∞ < t < ∞ . При 0 ≤ t < 2π получаем первую арку циклоиды. Укажем, что длина дуги ОА1О1=8а, а площадь одной арки S=3πa2.

Аналитическая геометрия на плоскости

81

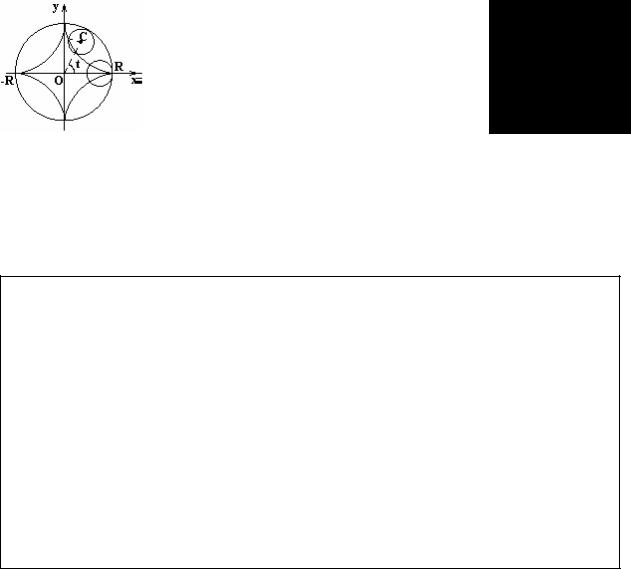
6.6.3*. Астроида

Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R.

x = R cos3 t,

Параметрические уравнения астроиды

y = R sin3 t,

где 0 ≤ t < 2π.

В декартовых координатах уравнение астроиды

x2/3+y2/3=R2/3.

Длина астроиды L=6R, а площадь, ограниченная астроидой, S=3πR2/8.

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

виды уравнений прямой на плоскости, преобразования от одного вида к другому;

канонические уравнения кривых второго порядка;

полярные координаты на плоскости, их связь с декартовыми;

параметрический способ задания линии.

Студент должен уметь:

решать простейшие задачи аналитической геометрии на плоскости;

находить элементы кривой второго порядка по ее

каноническому уравнению;

преобразовывать уравнения кривых от декартовых координат

кполярным и обратно;

преобразовывать параметрические уравнения кривой в декартовы

иобратно.

Лекция 7 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

В лекции 7 излагаются элементы общей теории поверхностей и подробно рассматриваются поверхности второго порядка, для исследования формы которых применяется метод сечений.

7.1.Поверхности

7.2.Линейчатые поверхности

7.3.Поверхности вращения

7.4.Поверхности второго порядка

7.5.Исследование формы поверхностей второго порядка по их каноническим уравнениям

7.5.1.Эллипсоид

7.5.2.Однополостный гиперболоид

7.5.3.Двуполостный гиперболоид

7.5.4.Эллиптический параболоид

7.5.5.Гиперболический параболоид

7.5.6.Конус

7.5.7.Эллиптический цилиндр

7.5.8.Гиперболический цилиндр

7.5.9.Параболический цилиндр

7.1.Поверхности

ОПоверхность в трехмерном пространстве можно определить следующим образом:

в явной форме:

	z = z (x, y); (x, y) G ;					(1)
в неявной форме:
F (x, y, z)= 0; (x, y, z) U;						(2)
в параметрической форме:
x = x(u,v),		y = y (u,v),		z = z (u,v); (u,v) G		(3)
в векторной форме:	G	G	(u,v); (u,v) G ,			(4)
	r = r
где G - плоская область, U - пространственная область.
G		G	G	G	- радиус-вектор точки по-
В формуле (4) r = x(u,v)i + y (u,v) j + z (u,v)k

верхности M (x, y, z).

Аналитическая геометрия. Поверхности второго порядка

83

7.2. Линейчатые поверхности

ОПоверхность называется линейчатой, если она получается при движении в пространстве прямой, называемой образующей.

ОКоническая поверхность возникает, когда образующая движется по некоторой плоской кривой, называемой направляющей, и имеет неподвижную точку, называемую вершиной.

ОЦилиндрическая поверхность возникает, когда фиксированная точка образующей движется по некоторой плоской кривой, называемой направляющей; в процессе перемещения образующая остается параллельной заданному направлению.

Кроме конических и цилиндрических поверхностей к линейчатым относятся однополостный гиперболоид и гиперболический параболоид, но закон движения образующей в этих случаях более сложен; ниже, при исследовании формы конкретных поверхностей, этот вопрос будет рассмотрен детально.

7.3. Поверхности вращения

Если поверхность получается вращением плоской кривой, лежащей в одной из координатных плоскостей вокруг одной из координатных осей, то уравнение поверхности может быть получено из уравнения линии:

1)кривая L(x, y)= 0 , лежащая в плоскости Oxy ;

вращение вокруг оси Ox :	F (x, y, z)= L(x, ± y2 + z2 )= 0 ,
вращение вокруг оси Oy :	F (x, y, z)= L(± x2 + z2 , y)= 0 ;

2)кривая L(x, z)= 0 , лежащая в плоскости Oxz ;

вращение вокруг оси Ox :	F (x, y, z)= L(x, ± y2 + z2 )= 0	,
вращение вокруг оси O z :	F (x, y, z)= L(± x2 + y2 , z)= 0	;

3)кривая L(y, z) = 0 , лежащая в плоскости Oyz ;

вращение вокруг оси Oy :	F (x, y, z)= L(y, ± x2 + z2 )= 0	,
вращение вокруг оси O z :	F (x, y, z)= L(± x2 + y2 , z)= 0	;

84

Лекция 7

7.4. Поверхности второго порядка

ОАлгебраической поверхностью второго порядка называется поверх-

ность S , уравнение которой в декартовой системе координат имеет вид:

a x2	+ a	22	y2	+ a z2	+ 2a xy + 2a xz + 2a		23	yz +
11				33	12	13			(5)
+2a14 x +		2a24 y + 2a34 z + a44 = 0,

где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае (5) – алгебраическая поверхность первого порядка, т.е. плоскость).

В зависимости от значений коэффициентов возможны случаи, когда уравнение (5) определяет вырожденную поверхность (пустое множество, точку, прямую, плоскость, пару плоскостей).

Например, уравнение x2 + y2 + z2 +1 = 0 не имеет решений и задает пус-

тое множество, уравнение	x2 + y2 + z2 = 0 задает точку с координатами
(0,0,0), уравнение x2 + y2 = 0	определяет прямую – координатную ось Oz ,

x2 = 0 задает координатную плоскость x = 0 , уравнение x2 =1 задает пару плоскостей x = −1 и x =1.

Далее будем рассматривать только невырожденные поверхности. Поверхности второго порядка обладают определенными элементами

симметрии. Некоторые имеют центр симметрии; все имеют хотя бы одну

плоскость симметрии; многие имеют ось симметрии.

Всякое уравнение вида (5) посредством преобразования координат, т.е. сдвигов и поворотов (так называемое приведение к главным осям), можно привести к каноническому виду. В уравнении канонического вида каждая переменная содержится только в одной степени: либо только в нулевой, либо только в первой, либо только во второй. Канонический вид уравнение принимает, когда оси системы координат совпадают с осями симметрии поверхности, а начало системы координат выбрано специальным образом (для цен- трально-симметричных поверхностей совпадает с центром симметрии).

7.5. Исследование формы поверхностей второго порядка по их каноническим уравнениям

Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями:

x = const; y = const; z = const.

Последовательно рассмотрим канонические уравнения поверхностей второго порядка.