
- •1. Формула Тейлора 2-го порядка с остаточным членом в форме Пеано для функции нескольких переменных.
- •2. Теорема о смешанных производных.
- •7.3.1. Теорема о смешанных производных
- •3. Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной.
- •4. Формула Тейлора с остаточным членом в форме Лагранжа для функции нескольких переменных.
- •5. Критерий выпуклости функции. Доказательство . Следствие.
- •6. Критерий выпуклости функции. Доказательство . Следствие.
- •7. Лемма о знакопостоянной функции .
- •8. Необходимое условие глобального экстремума функции.
- •8.3.2. Необходимое условие глобального экстремума
- •9. Метод Лагранжа отыскания экстремумов (доказательство теоремы).
- •10. Лемма о системе линейных уравнений. Следствие.
- •1. Лемма о многочлене Тейлора .
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •3. Вывод формулы для . Частный случай для.
- •4. Асимптоты функции.
- •5. Разложение синуса по формуле Маклорена.
- •6. Разложение косинуса по формуле Маклорена.
- •7. Условие строгой монотонности функции (1-е утверждение теоремы 8.1).Теорема
- •8. Условие нестрогой монотонности функции (2-е утверждение теоремы 8.1).
- •9. Необходимое условие экстремума функции нескольких переменных.
- •10. Достаточное условие экстремума функции нескольких переменных.
3. Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной.
Пусть
функция
 раз дифференцируема в точке
раз дифференцируема в точке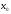 .
Многочлен
.
Многочлен
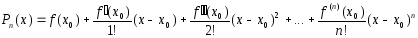 (1)
(1)
называется
многочленом
Тейлора порядка
 для функции
для функции
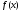 в точке
в точке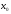 .
.
Лемма.
Если
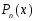 является многочленом Тейлора для функции
является многочленом Тейлора для функции
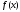 вточке
вточке
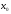 ,
то справедливы следующие утверждения:
,
то справедливы следующие утверждения:
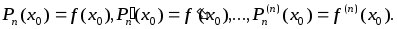
Доказательство.
Найдем все производные многочлена
Тейлора, который запишем в виде
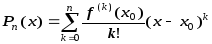 ,
где
,
где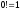 ,
,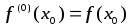 :
:
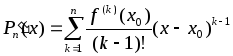
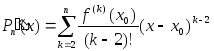
………………………….
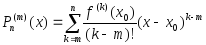
…………………………..
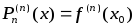 ,
,
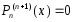 .
.
Отсюда
следует, что
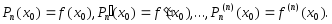 ■
■
Теорема
7.1.
Пусть функция

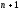 раз дифференцируема в окрестности
раз дифференцируема в окрестности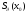 точки
точки .
Тогда для любого
.
Тогда для любого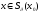 справедлива формула
справедлива формула
 ,
,
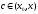 .
(2)
.
(2)
Доказательство.
Рассмотрим
функцию
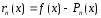 .
Теорема будет доказана, если установить,
что
.
Теорема будет доказана, если установить,
что
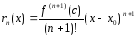 ,
,
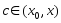 .
.
Так
как функции
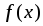 и
и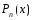
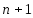 раз дифференцируемы в окрестности
раз дифференцируемы в окрестности ,
то и функция
,
то и функция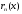 также
также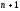 раз дифференцируема в этой окрестности.
Из леммы следует, что
раз дифференцируема в этой окрестности.
Из леммы следует, что
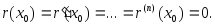
Рассмотрим
функцию
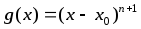 .
Тогда
.
Тогда
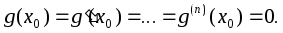
Для
пары функций
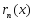 и
и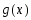 выполняются условия леммы из § 5.5. Из
этой леммы следует, что
выполняются условия леммы из § 5.5. Из
этой леммы следует, что
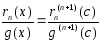 ,
,
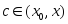 .
.
Так
как
 ,
,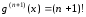 ,
то
,
то
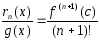
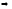
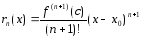 ,
,
где
точка
 лежит между точками
лежит между точками и
и .■
.■
Функция
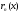 называетсяостаточным
членом формулы Тейлора,
а формула (2) называется формулой Тейлора
порядка
называетсяостаточным
членом формулы Тейлора,
а формула (2) называется формулой Тейлора
порядка
 с остаточным
членом в форме Лагранжа.
Так как точка
с остаточным
членом в форме Лагранжа.
Так как точка
 является внутренней точкой отрезка
является внутренней точкой отрезка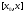 ,
то найдется такое число
,
то найдется такое число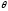 ,
,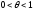 ,
что
,
что .
Теперь остаточный член в форме Лагранжа
можно записать в виде
.
Теперь остаточный член в форме Лагранжа
можно записать в виде
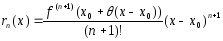 ,
,
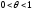 .
.
4. Формула Тейлора с остаточным членом в форме Лагранжа для функции нескольких переменных.
Теорема
7.2. Если
функция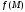 в окрестности
в окрестности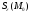 точки
точки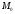 имеет непрерывные частные производные
до
имеет непрерывные частные производные
до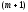 -го
порядка включительно, то
-го
порядка включительно, то
справедлива формула Тейлора с остаточным членом в форме Лагранжа
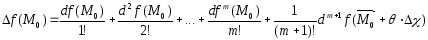 ,
,
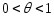 .
(1)
.
(1)
Доказательство.
Придадим переменным
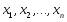 такие приращения
такие приращения ,
чтобы точка
,
чтобы точка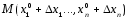 принадлежала окрестности
принадлежала окрестности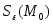 .
Рассмотрим сложную функцию от одной
переменной
.
Рассмотрим сложную функцию от одной
переменной :
:
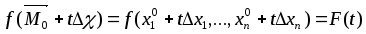 .
(2)
.
(2)
Теперь
запишем формулу Маклорена для функции
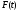 с остаточным членом в форме Лагранжа:
с остаточным членом в форме Лагранжа:
 ,
,
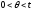 .
.
Отсюда
при
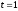 получаем
получаем
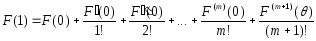 ,
,
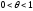 .
(3)
.
(3)
Из равенства (2) и следствия из теоремы 6.5 имеем:
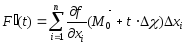
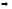

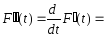
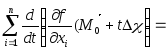
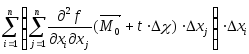
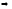
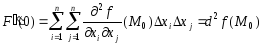 .
.
Продолжая таким образом далее, получим
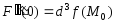 ,
. . . ,
,
. . . ,
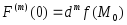 .
.
Так
как
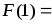
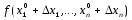 ,
,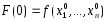 ,
то
,
то

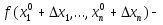
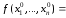
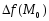 ,
,
Теперь из формулы (3) следует
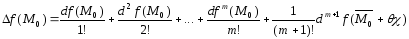
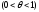 .
.
5. Критерий выпуклости функции. Доказательство . Следствие.
Теорема
8.4. Функция
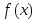 дифференцируема на интервале
дифференцируема на интервале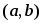 .
Следующие
условия равносильны.
.
Следующие
условия равносильны.
1.
Функция
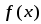 выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
 .
.
2.
Производная
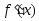 не возрастает
(не убывает)
на интервале
не возрастает
(не убывает)
на интервале
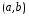 .
.
Доказательство
1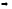 2.Возьмем на
интервале
2.Возьмем на
интервале
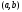 произвольные точки
произвольные точки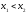 .
Проведем
.
Проведем
касательную
к графику функции
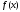 в точке
в точке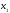 .
Тогда из выпуклости функции вверх (вниз)
следует
.
Тогда из выпуклости функции вверх (вниз)
следует
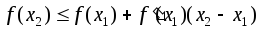
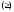 (2)
(2)
Теперь
проведем касательную к графику функции
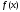 в точке
в точке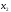 .
Тогда из выпуклости функции вверх (вниз)
следует
.
Тогда из выпуклости функции вверх (вниз)
следует
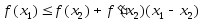
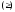 .
(3)
.
(3)
Сложим неравенства (2) и (3), и после простых преобразований получим
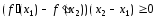

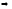
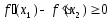
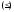
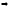
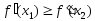
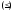 .
.
Итак,
если
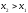 ,
то
,
то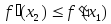
 ,
т.е. производная
,
т.е. производная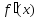 является невозрастающей (неубывающей)
функцией.
является невозрастающей (неубывающей)
функцией.
Следствие.
Функция
 дважды дифференцируема на интервале
дважды дифференцируема на интервале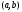 .
Тогда равносильны условия.
.
Тогда равносильны условия.
1.
Функция
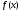 выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
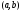 .
.
2.
Вторая
производная неположительна (неотрицательна)
на интервале
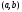 .
.
Доказательство. Используя теорему 8.4 и второе утверждение теоремы 8.1, в котором роль функции играет производная, получим следующую цепочку равносильных утверждений:
функция
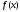 выпукла вверх
(вниз)
на интервале
выпукла вверх
(вниз)
на интервале
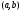
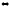
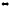 производная
производная
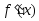 не возрастает (не убывает) на интервале
не возрастает (не убывает) на интервале
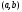
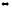
 производная
производная
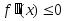
 на интервале
на интервале
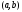 .
■
.
■
