
- •1. Формула Тейлора 2-го порядка с остаточным членом в форме Пеано для функции нескольких переменных.
- •2. Теорема о смешанных производных.
- •7.3.1. Теорема о смешанных производных
- •3. Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной.
- •4. Формула Тейлора с остаточным членом в форме Лагранжа для функции нескольких переменных.
- •5. Критерий выпуклости функции. Доказательство . Следствие.
- •6. Критерий выпуклости функции. Доказательство . Следствие.
- •7. Лемма о знакопостоянной функции .
- •8. Необходимое условие глобального экстремума функции.
- •8.3.2. Необходимое условие глобального экстремума
- •9. Метод Лагранжа отыскания экстремумов (доказательство теоремы).
- •10. Лемма о системе линейных уравнений. Следствие.
- •1. Лемма о многочлене Тейлора .
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •3. Вывод формулы для . Частный случай для.
- •4. Асимптоты функции.
- •5. Разложение синуса по формуле Маклорена.
- •6. Разложение косинуса по формуле Маклорена.
- •7. Условие строгой монотонности функции (1-е утверждение теоремы 8.1).Теорема
- •8. Условие нестрогой монотонности функции (2-е утверждение теоремы 8.1).
- •9. Необходимое условие экстремума функции нескольких переменных.
- •10. Достаточное условие экстремума функции нескольких переменных.
6. Критерий выпуклости функции. Доказательство . Следствие.
Теорема
8.4. Функция
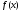 дифференцируема на интервале
дифференцируема на интервале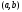 .
Следующие
условия равносильны.
.
Следующие
условия равносильны.
1.
Функция
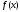 выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
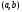 .
.
2.
Производная
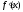 не возрастает
(не убывает)
на интервале
не возрастает
(не убывает)
на интервале
 .
.
Доказательство
2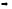 1.Возьмем
произвольную точку
1.Возьмем
произвольную точку
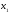 на интервале
на интервале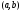 и покажем, что график функции находится
под (над) касательной, проведенной в
точке
и покажем, что график функции находится
под (над) касательной, проведенной в
точке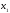 ,
т.е.
,
т.е.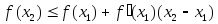
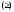 для любой точки
для любой точки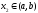 .
Возможны два случая:
.
Возможны два случая:
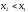 или
или
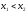 .
.
Если
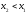 ,
то, применяя теорему Лагранжа на отрезке
,
то, применяя теорему Лагранжа на отрезке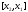 ,
получим
,
получим
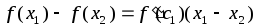 ,
,
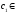
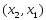 .
(4)
.
(4)
Так
как производная
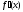 является невозрастающей (неубывающей)
функцией, то из
является невозрастающей (неубывающей)
функцией, то из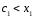 следует
следует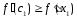
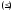 .
Отсюда и равенства (4) имеем
.
Отсюда и равенства (4) имеем
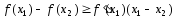
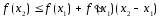
 .
.
Если
же
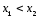 ,
то, применяя теорему Лагранжа на отрезке
,
то, применяя теорему Лагранжа на отрезке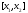 ,
получим
,
получим
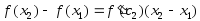 ,
,
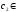
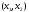 .
(5)
.
(5)
Так
как производная
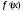 является невозрастающей (неубывающей)
функцией, то из неравенства
является невозрастающей (неубывающей)
функцией, то из неравенства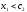 следует
следует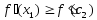
 .
Отсюда и равенства (5) имеем
.
Отсюда и равенства (5) имеем
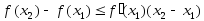
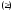
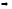
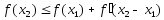
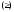 .
■
.
■
Следствие.
Функция
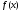 дважды дифференцируема на интервале
дважды дифференцируема на интервале .
Тогда равносильны условия.
.
Тогда равносильны условия.
1.
Функция
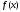 выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
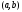 .
.
2.
Вторая
производная неположительна (неотрицательна)
на интервале
 .
.
Доказательство. Используя теорему 8.4 и второе утверждение теоремы 8.1, в котором роль функции играет производная, получим следующую цепочку равносильных утверждений:
функция
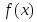 выпукла вверх
(вниз)
на интервале
выпукла вверх
(вниз)
на интервале
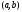
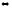
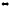 производная
производная
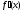 не возрастает (не убывает) на интервале
не возрастает (не убывает) на интервале
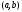

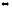 производная
производная
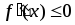
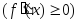 на интервале
на интервале
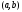 .
■
.
■
7. Лемма о знакопостоянной функции .
Лемма
1 . Если
функция
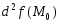 является
знакопостоянной и
является
знакопостоянной и
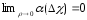 ,
то найдется
такое число
,
то найдется
такое число
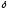 ,
что знак выражения
,
что знак выражения
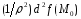
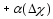 (3)
(3)
совпадает
со знаком
функции
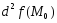 ,
если
,
если
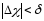 .
.
Доказательство. Перепишем формулу (2) в виде
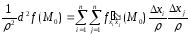 .
.
Так как
 ,
,
то
точка
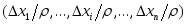 при любых значениях
при любых значениях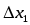 ,…,
,…,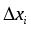 ,…,
,…,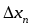 ,
одновременно не равных нулю, принадлежит
сфере
,
одновременно не равных нулю, принадлежит
сфере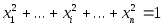 .
.
Квадратичная
функция
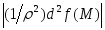 непрерывна при любых значениях
непрерывна при любых значениях
переменных,
и значит, непрерывна на сфере, которая
является замкнутым и ограниченным
множеством (следствие из теоремы 4.9) .
Так как функция
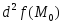 является знакоопределенной, то
является знакоопределенной, то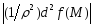 >0
в каждой точке сферы.
>0
в каждой точке сферы.
Из
2-й теоремы Вейерштрасса следует, что
функция
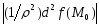 принимает свое наименьшее значение
принимает свое наименьшее значение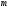 в некоторой точке сферы, которое больше
нуля, т.е.
в некоторой точке сферы, которое больше
нуля, т.е.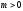 .
Отсюда следует, что
.
Отсюда следует, что
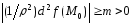 .
(4)
.
(4)
Так
как
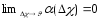 ,
то из теоремы 3.11 вытекает, что если
,
то из теоремы 3.11 вытекает, что если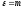 ,
то найдется такое число
,
то найдется такое число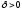 ,
что неравенство
,
что неравенство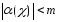 будет справедливо, как только
будет справедливо, как только .
Отсюда следует, что
.
Отсюда следует, что
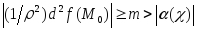 .
.
Следовательно,
знак выражения
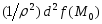
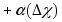 совпадает со знаком
совпадает со знаком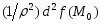 ,
как только
,
как только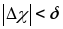 .■
.■
8. Необходимое условие глобального экстремума функции.
8.3.2. Необходимое условие глобального экстремума
Лемма.
Система
уравнений
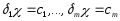 ,
,
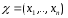 ,имеет
решения при любых значениях
,имеет
решения при любых значениях
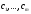 ,
если векторы
,
если векторы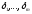 линейно независимы.
линейно независимы.
Доказательство леммы приводится в приложении 3. ■
Следствие.
Если система векторов
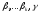 линейно независима, то найдется такой
вектор
линейно независима, то найдется такой
вектор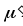
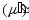 ,
что
,
что
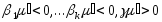 (
(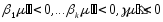 ).
(1)
).
(1)
Доказательство. Из леммы следует, что система уравнений
 (
(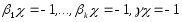 )
)
имеет
решение

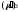 ,
которое удовлетворяет условию (1).■
,
которое удовлетворяет условию (1).■
Теорема
8.10
(необходимое
условие глобального экстремума функции).
Функция
 определена на множестве
определена на множестве
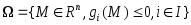 ,
,
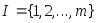 .
.
Функции
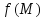 и
и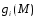 при любом
при любом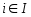 дифференцируемы
в точке глобального экстремума
дифференцируемы
в точке глобального экстремума
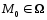 функции
функции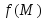 ,.
Тогда система векторов
,.
Тогда система векторов
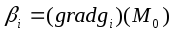 ,
,
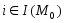 ;
;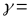
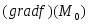 ,
,
где
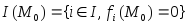 ,
линейно зависима.
,
линейно зависима.
Доказательство от противного, т.е. пусть система векторов
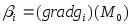 ,
,
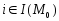 ;
;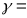
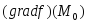
линейно
независима. Из следствия к лемме следует,
что найдется такой вектор
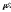
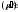 ,
что
,
что
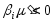 ,
,
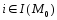 ,
,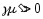 (
(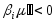 ,
,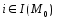 ,
,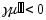 ).
).
Так
как
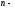 мерный
вектор
мерный
вектор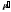
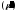 удовлетворяет условию
удовлетворяет условию
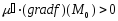
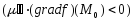 ,
,
то
из свойства градиента следует, что можно
построить такое число
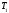 ,
что при всех
,
что при всех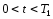
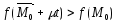
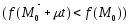 .
(2)
.
(2)
Так
как
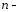 мерный
вектор
мерный
вектор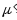
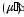 удовлетворяет условию
удовлетворяет условию
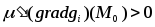 ,
,
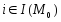 ,
(
,
( ,
,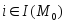 ),
),
то
можно построить такое число
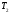 (теорема
6.9), что при всех
(теорема
6.9), что при всех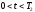 точка
точка
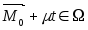 (3)
(3)
Обозначим
символом
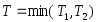 .
Тогда при всех
.
Тогда при всех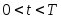 условия (2) и (3) справедливы, что противоречит
определению глобального экстремума.■
условия (2) и (3) справедливы, что противоречит
определению глобального экстремума.■
