10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.

О-я: Числовий ряд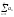- наз-ся знакододатнім або додатнім, якщо а_n, n

Аналогічно модна розглянути означення відємного ряду.

Заув-я:

З властивості 1 числових рядів випливає, що дослідження відємного ряду одразу можна звести до дослідження відповідного додатньного ряду, якщо винести мінус за знак суми.

Тому надалі розглядатимемо лише додатні ряди.

Теорема1(ознаки порівняння)

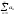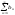Нехай і- додатні ряди і дляn викон-ся нер-ть 0 а_n b_n (1) то із збіжності ряду 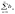(2) випливає збіжність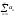(3) ,а розбіжності 3 випливає розб-ть 2.

Враховуючи властивість (3) теорема 1 працює і у тому випадку, якщо нерівність (3)виконується не для всіх n, а починаючи з деякого . При застосуванні цієї ознаки на практиці частіше частіше всього досліджуваний ряд порівнюють з рядами, збіжність або розбіжність яких вже відома. До них відносяться: геометрична прогресія

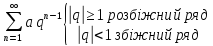
Узагальнений гармонічний ряд: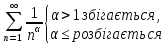

Т-ма2(гранична ознака порівняння)

Якщо задані 2 додатні числові ряда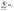(1) ,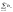(2) існує границяlim_n а_n/b_n=к, де 0<к<+, то ряди (1) і (2) збігаються або розбігаються одночасно, тобто мають однакову поведінку.

б). Оз-наки Д’аламбера і Коши.

Теорема 3 (ознака Д’аламбера):Нехай задано додатній числовий ряд 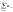(1). Якщо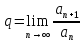 і q, то ряд (1) збіжний, q - ряд (1) розбіжний.

Теорема 4 (ознака Коши): Нехай для додатного ряду 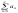існує границя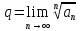, тоді якщо 0≤q даний ряд збіжний, q - ряд розбіжний.

Зауваження: Ознаки Д’аламбера і Коши рівносильні у тому розумінні, що коли 1 з цих ознак не дає відповіді на питання про збіжність (q=1), то інша ознака теж дає q=1. Для дослідження питання про збіжність або розбіжність ряду в цьому випадку застосовують інші ознаки.

в). Інтегральна ознака. Ознака Раабе.

Теорема5 (Інтегральна ознака): Нехай задано числовий ряд 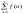(1), члени якого є значеннями неперервної додатної і монотонноспадної ф-їf(x) на [1,+), тоді ряд (1) збігається, якщо збігається невласний інтеграл , і ряд (1) розбігається, якщо цей інтеграл розбіжний.

Теорема6: (ознака Раабе) Якщо 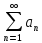– додатній числовий ряд і 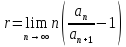, то колиr>1 ряд збігається, а коли r<1 ряд розбігається.

11. Знакопочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.

Озн.: числовий ряд назив. знакопочередним якщо знаки його членів строго передуються. Тобто будь-які два сусідні члени мають різні знаки: а₁-а₂+а₃-...+(-1)^n-1a_n+…=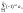 (1)

де a_n0, n>N.

Теорема 1 (ознака Лейбніца): Ряд (1) збіжний якщо1) lim_n а_n=0 2) а_n > а_n+1, n>N

Доведення: Розглянемо послідовність частинних сум ряду (1) з парним числом членів S_2n=а₁-а₂+а₃-a₄+...+a_2n-1-a_2n= (а₁-а₂)+(а₃-a₄)+...+(a_2n-1-a_2n)>0< а₁ Послідовність {S_2n} складається з додатних членів, крім того S_2n=a₁-[(а₂-а₃)+(а₄-a₅)+...+(a_2n-2-a_2n-1)+a_2n]  а₁. Оскільки весь вираз у квадратних дужках додатній тобто послідовність тобто посл-ть {S_2n}, крім того що складається з додатних членів є ще зростаючою і обмеженою зверху. За теоремою про границю обмеженої послідовності ця послідовність має границю: lim_n S_2n = S_.

Розглянемо тепер частинну суму S_2n+1 з непарним числом членів S_2n+1= S_2n+а_2n+1. (2) Перейшовши у (2) до границі при n→∞ і враховуючи першу умову теореми одержимо: lim_n S_2n+1 = lim_n S_2n+ lim_n а_2n+1 = S+0=S . Ми одержали, що lim_n S_2n+1 = lim_n S_2n = S це і означає, що lim_n S_n=S Тобто ряд(1) за озн збіжний. Теор доведено

Озн: Числовий ряд 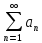назив знакозмінним якщо він містить нескінчену к-сть як додатних так і від’ємних членів

Очевидно, що розглянуті вище знакопочередні ряди є частим випадком знакозмінних рядів. Що до знакозмінних рядів справедлива наступна теорема

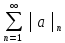Теорема 2: Нехай знакозміний ряд. Якщо збігається ряд, то збігається ряд.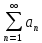

Твердження обернене до данної теореми неправильне: існують знакозмінні ряди 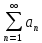які збігаються але ряди складені з модулів їх членів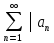│є розбіжними.

Прикладом такого ряду є ряд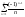

Ми довели, що він збіжний за ознакою Лейбніца. Але ряд з модулів 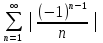=. 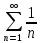є розбіжним гармонічним рядом. Зв’язку з цим по аналогії як це було у невласних інтегралах існують абсолютні і умовні збіжності.

О-ня 1: Якщо разом з рядом . 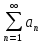збігається 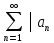ряд│ ряд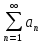називається збіжним абсолютно.

У випадку якщо ряд 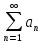збіжний а 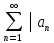ряд│ розбігається, то ряд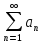називається збіжним умовно.