
- •Диференціальні рівняння
- •5.04030101 «Прикладна математика»
- •5.05010301 «Розробка програмного забезпечення»
- •Зміст дисципліни
- •Тема 1. Диференціальні рівняння: основні поняття і означення
- •Тема 2. Диференціальні рівняння першого порядку
- •2.2. Рівняння з подільними змінними
- •2.3. Однорідні диференціальні рівняння
- •2.4. Лінійні рівняння
- •2.4. Рівняння в повних диференціалах
- •Тема 3. Диференціальні рівняння вищих порядків
- •3.1. Рівняння, що допускають зниження порядку
- •3.1.1. Диференціальні рівняння виду
- •3.1.2. Рівняння другого порядку, які не містять невідомої функції
- •3.1.3. Рівняння другого порядку, які не містять незалежної змінної
- •3.2. Лінійні диференціальні рівняння вищих порядків
- •3.2.1. Лінійні однорідні рівняння го порядку.
- •Системи диференціальних рівнянь
- •Робота з підручниками та навчльними посібниками
- •Консультації
- •Лекції та практичні заняття
- •Екзамен
- •Методичні вказівки до виконання та оформлення домашньої контрольної роботи
- •Варіанти завдань домашньої контрольної роботи
Тема 2. Диференціальні рівняння першого порядку
Диференціальне
рівняння І порядку в загальному вигляді
може бути записане так:
![]() .
Якщо таке рівняння розрішити відносно
похідної
.
Якщо таке рівняння розрішити відносно
похідної![]() ,
то його можна подати у вигляді
,
то його можна подати у вигляді![]() .
.
Загальним
рішенням (загальним інтегралом) рівняння
першого порядку є функція
![]() ,
,![]() ,
яка задовольняє рівнянню при будь –
яких значеннях довільної константи
,
яка задовольняє рівнянню при будь –
яких значеннях довільної константи![]() .
.
Отже,
для знаходження частинного рішення
рівняння І порядку слід знайти значення
лише однієї константи
![]() .
Для цього достатньо задати єдину
початкову умову
.
Для цього достатньо задати єдину
початкову умову![]() ,
розв’язати
задачу Коші і знайдене значення
,
розв’язати
задачу Коші і знайдене значення
![]() підставити в загальне рішення. В
результаті отримаємо частинне рішення
підставити в загальне рішення. В
результаті отримаємо частинне рішення![]() ,
яке задовольняє початковій умові
,
яке задовольняє початковій умові![]() .
.
Розглянемо основні типи диференціальних рівнянь І порядку.
2.1.
Рівняння
![]() ,
яке може бути розв’язане шляхом простого
інтегрування обох частин рівняння,
тобто
,
яке може бути розв’язане шляхом простого
інтегрування обох частин рівняння,
тобто![]() .
.
Приклад
1. Знайти
частинне рішення рівняння
![]() ,
якщо
,
якщо![]() .
.
Розв’язання.
![]() .При
.При
![]() знаходимо:
знаходимо:![]() Підставимо знайдене значення
Підставимо знайдене значення![]() в загальне рішення і отримаємо частинне
рішення
в загальне рішення і отримаємо частинне
рішення![]() .
.
Відповідь:
![]() .
.
2.2. Рівняння з подільними змінними
Означення. Диференціальним рівнянням з подільними змінними називається рівняння
![]() , (1.1)
, (1.1)
або
![]() . (1.2)
. (1.2)
Поділимо
обидві частини рівняння (1.1) на добуток
![]() і
отримаємо рівняння
і
отримаємо рівняння
![]() . (1.3)
. (1.3)
Позначимо
![]() ,
тоді
перейдемо к рівнянню
,
тоді
перейдемо к рівнянню
![]() з поділеними змінними,
в якому кожне з двох доданків в лівій
частині залежить лише від однієї змінної.
Інтегруючи почленно останню рівність,
знайдемо загальний інтеграл даного
рівняння
з поділеними змінними,
в якому кожне з двох доданків в лівій
частині залежить лише від однієї змінної.
Інтегруючи почленно останню рівність,
знайдемо загальний інтеграл даного
рівняння
![]() .
.
Приклад
2. Розв’язати
рівняння
![]() ,
якщо
,
якщо![]() .
.
Розв’язання.
Замінимо
![]() і помножимо обидві частини рівняння на
і помножимо обидві частини рівняння на![]() :
:
![]() .
.
Поділимо
обидві частини рівняння на добуток
![]() :
:
![]() .
.
Проінтегруємо обидві частини рівняння:
![]() .
.
![]() ;
;
![]() .
Отримаємо
.
Отримаємо
![]() .
.
Помножимо
обидві частини рівняння на
![]() і скористуємося властивостями логарифмів:
і скористуємося властивостями логарифмів:

Потенціюючи, знаходимо:
![]() ,
,
звідки отримаємо загальне рішення рівняння:
![]() .
.
Розв’яжемо
задачу Коші при
![]() :
:![]() .
.
Підставимо
значення
![]() в загальне рішення рівняння і остаточно
знайдемо частинне рішення рівняння:
в загальне рішення рівняння і остаточно
знайдемо частинне рішення рівняння:
![]() .
.
Відповідь.
![]() .
.
2.3. Однорідні диференціальні рівняння
Означення
1. Функція
![]() називаєтьсяоднорідною
функцією
називаєтьсяоднорідною
функцією
![]() го
виміру,
якщо для будь – якого
го
виміру,
якщо для будь – якого
![]() виконується рівність
виконується рівність
![]() .
.
Приклад
3. Функція
![]() є однорідною функцією третього виміру,
бо
є однорідною функцією третього виміру,
бо![]() .
.
Функція
![]() є однорідною функцією нульового виміру,
тому що
є однорідною функцією нульового виміру,
тому що![]() .
.
Завдання
1. Доведіть,
що функція
![]() є
однорідною функцією першого виміру, а
функція
є
однорідною функцією першого виміру, а
функція![]() є однорідною функцією другого виміру.
є однорідною функцією другого виміру.
Означення 2. Диференціальне рівняння першого порядку
![]() , (1.4)
, (1.4)
називається
однорідним,
якщо функція
![]() є однорідною функцією нульового виміру
відносно
є однорідною функцією нульового виміру
відносно![]() і
і![]() .
.
Отже,
згідно з означенням,
![]() для
будь – якого
для
будь – якого![]() .
Оберемо
.
Оберемо![]() і отримаємо
і отримаємо![]() ,
тобто
,
тобто![]() і функція
і функція![]() залежить лише від відношення аргументів
залежить лише від відношення аргументів![]() .
Тому рівняння (1.4) може бути записане у
вигляді
.
Тому рівняння (1.4) може бути записане у
вигляді
![]() . (1.5)
. (1.5)
Введемо
допоміжну функцію
![]() ,
і оскільки
,
і оскільки![]() ,
то
,
то![]() .
Отримаємо рівняння з подільними змінними
.
Отримаємо рівняння з подільними змінними
![]() . (1.6)
. (1.6)
Розв’яжемо
його:
![]()
![]()
![]()
![]() Далі
знаходимо інтеграл в лівій частині
рівняння, замінюємо в ньому
Далі
знаходимо інтеграл в лівій частині
рівняння, замінюємо в ньому
![]() і отримаємо загальний інтеграл
і отримаємо загальний інтеграл![]() рівняння (1.4).
рівняння (1.4).
Для того, щоб розв’язати однорідне рівняння, необхідно:
Переконатися в тому, що рівняння однорідне, і записати його у вигляді (1.4).
Покласти
 ,
,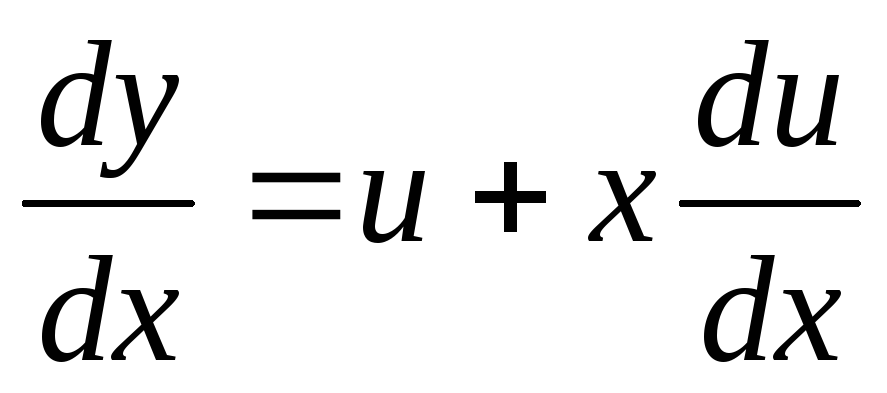 .
.Скоротити дріб на
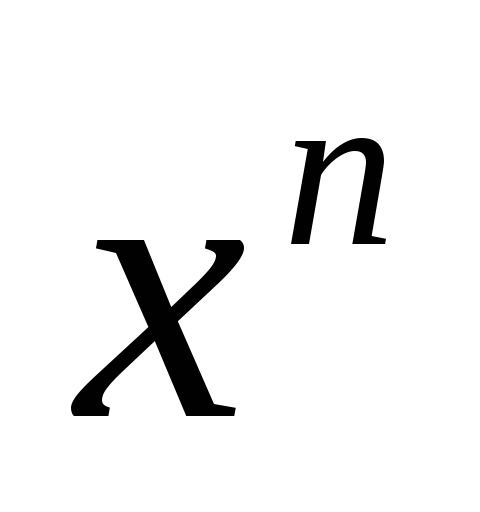 (повністю),
перенести
(повністю),
перенести в ліву частину і спростити її.
в ліву частину і спростити її.Розділити змінні (справа завжди
 )
і про інтегрувати.
)
і про інтегрувати.Замінити
 і спростити.
і спростити.
Зауважимо,
що рівняння
![]() є однорідним, якщо
є однорідним, якщо![]() і
і![]() є
однорідними функціями однакового
виміру.
є
однорідними функціями однакового
виміру.
Приклад 4.
Знайти загальний інтеграл рівняння
![]() .
.
Розв’язання.
![]()

Оскільки
![]() ,
то функція
,
то функція![]() єоднорідною
функцією нульового виміру, і задане
рівняння є однорідним.
єоднорідною
функцією нульового виміру, і задане
рівняння є однорідним.

![]()

Відповідь. ![]() .
.
Приклад 5.
Проінтегрувати рівняння
![]() .
.
Розв’язання.
Оскільки
функції ![]() і
і ![]() є однорідними
функціями другого виміру (переконайтеся
самостійно), то задане рівняння є
однорідним.
є однорідними
функціями другого виміру (переконайтеся
самостійно), то задане рівняння є
однорідним.

![]()

Відповідь. ![]() .
.
Приклад 6.
Розв’язати
задачу Коші
![]() ,
якщо
,
якщо![]() .
.
Розв’язання. ![]()

Права частина
рівняння містить функцію, яка залежить
лише від відношення аргументів
![]() ,
тому рівняння є однорідним.
,
тому рівняння є однорідним.

Якщо
![]() ,
то
,
то![]() ,
звідки
,
звідки
![]() .
Отримаємо
.
Отримаємо

Відповідь. ![]() .
.
