2.4. Лінійні рівняння

Означення. Диференціальне рівняння називається лінійним, якщо воно є рівнянням першого степеню відносно невідомої функції та її похідноїі може бути записаним у вигляді

, (1.7)

де деякі функції.

Якщо в правій частині рівняння (1.7) функція , то рівнянняназиваєтьсялінійним однорідним і розв’язується як рівняння з подільними змінними.

Розглянемо випадок, коли . Тоді лінійне рівняння (1.7) зводиться к двом рівнянням з подільними змінними за допомогоюпідстановки Бернуллі , дедопоміжні функції змінної. Знайдемоі підставимоів рівняння (1):,

. (1.8)

Оскільки функції іобираються довільно, аби їх добуток задовольняв би рівнянню (1), то функціюоберемо так, щоб в рівнянні (1.8)

. (1.9)

Рівняння (1.9) є рівнянням з подільними змінними, з якого знаходимо :

; ; ;

. (1.10)

Довільну константу в цьому випадку вважаємо дорівнюючою нулю. Підставимо рівняння (1.9) в рівняння (1.8):

. (1.11)

З рівняння (1.11) дістанемо:

, або

. (1.12)

Замінюючи в формулі (1.12) функцію її виразом (1.10), отримаємо

. (1.13)

Помножимо наі отримаємо загальний інтеграл рівняння

. (1.14)

При розв’язанні лінійних рівнянь значно простіше запам’ятати і використовувати формули (1.10) і (1.12), ніж формулу (1.14).

Приклад 7. Розв’язати рівняння .

Розв’язання. Рівняння є лінійним відносно і, причому. За формулою (1.10) знаходимо. Далі, за формулою (1.12) обчислимо. Оскільки, то.

Відповідь. .

Приклад 8. Розв’язати задачу Коші , якщо.

Розв’язання. Рівняння є лінійним відносно і, причому.

; ;.

Якщо , то, звідки. Тоді.

Відповідь. .

2.4. Рівняння в повних диференціалах

Означення. Якщо в диференціальному рівнянні

(1.15)

ліва частина є повним диференціалом деякої функції від незалежних зміннихі, то таке рівняння називаєтьсядиференціальним рівнянням в повних диференціалах.

Інакше кажучи, рівняння (1.15) є рівнянням в повних диференціалах, якщо існує така функція , що

.

В цьому випадку диференціальне рівняння (1.15) можна подати у вигляді

(1.16)

і його загальний інтеграл

. (1.17)

Нехай функції івизначені і неперервні в деякій областіі мають в цій області неперервні частинні похідні поі по. Необхідною і достатньою умовою того, щоб рівняння (1.15) було рівнянням в повних диференціалах, є виконання рівності

. (1.18)

Якщо умова (1.18) виконана, то загальний інтеграл можна записати у вигляді

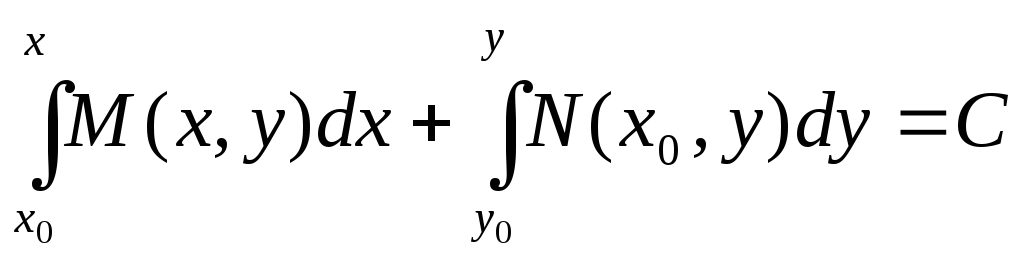, (1.19)

або

, (1.20)

де точка належить області. Тут інтегрування проводилося по одній із змінних, інша змінна є при цьому параметром.

Рішення задачі Коші з початковими умовами в області, за умови, що в точціфункціїіводночас не перетворюються на нуль, отримаємо із загального інтегралу (1.19) або (1.20) при:

, (1.21)

або

. (1.22)

Приклад 9. Проінтегрувати рівняння .

Розв’язання. В даному рівнянні . Знайдемо. Оскільки умовавиконується, то задане рівняння є рівнянням в повних диференціалах. Знайдемо загальний інтеграл рівняння, обираючи точку. За формулою (1.19) приотримаємо:

, .

Відповідь: .

Приклад 10. Розв’язати задачу Коші , якщо.

Розв’язання. .

.

, отже задане рівняння є рівнянням в повних диференціалах.

За формулою (1.21) при

, ,

,

.

Відповідь: .