Волк_Высшая математика.2010

9.3. Ряды Тейлора и Маклорена

Теорема. Если функция f (x) и ее производные всех порядков определены, непрерывны и ограничены на (a; b) , а точки х0 и х принадлежат этому интервалу, то на (a; b) функция f (x) представима степенным рядом

∞

f

(n )

(x0 )

f (x) = ∑

(x − x0 )n ,

(9.15)

n=0

n!

f (x).

который называется рядом Тейлора для функции

При x0 = 0 ряд Тейлора (8.15) называется рядом Маклорена и

формула (9.15) принимает вид

f (n ) (0) n

∞

f (x) = ∑

x

,

(9.16)

n!

n=0

или в развернутой формуле записи

f (x) = f (0)+

f ′(0)

x +

f ′′(0)

x2 +

f ′′′(0)

x3

+…+

f (n ) (0)

xn +… . (9.17)

2!

3!

1!

n!

Поскольку основные элементарные функции ex , sin x , cos x удовлетворяют условиям сформулированной выше теоремы на всей числовой прямой, то при любом x R имеют место следующие разложения:

∞

n

x

2

x

3

x

n

ex = ∑

x

=1+ x +

+…+

+…;

(9.18)

2!

n!

n=0 n!

3!

∞

(−1)n x2n+1

x3

x5

x7

n x2n+1

sin x = ∑

(2n +1)!

= x −

+

−

+

…+(−1)

+…;(9.19)

3!

5!

7!

(2n

+1)!

n=0

∞ (−1)n x2 n

x

2

x

4

x

6

n x2n

cos x = ∑

(2n)!

=1−

+

−

+…+ (−

1)

+… .

(9.20)

2!

4!

6!

(2n)!

n=0

Для −1 < x ≤1

∞

(−1)n+1 xn

x2

x3

x4

n+1

xn

ln(1 + x) = ∑

= x −

+

−

+…+(−1)

+… ,

(9.21)

n

2

3

4

n

n=0

а для −1 < x <1

111

m			m(m −1)		2		m(m −1)(m − 2)			3
(1 + x)	=1+ mx +		2!	x		+	3!		x		+…+
		m(m −1)(m − 2)…(m −(n −1))									(9.22)
	+							xn +… .
			n!

Приведенные разложения используются для приближенного вычисления определенных интегралов, для приближенного вычисления значений функций, для решения дифференциальных уравнений и т. д.

0,5

Задача 11. Вычислить определенный интеграл ∫ ln(1 + x2 )dx

0

с точностью до 0,001.

Решение. Так как разложение функции ln(1 + x) в ряд Маклорена имеет вид (9.21), то подставляя в это разложение вместо х переменную х2, получим:

ln(1+ x2 ) = x2 −	x4	+	x6	−	x8	+… .
2		3		4

Используя это разложение и почленно интегрируя, получим:

				0,5							1							x4					x6					x8
									2		2				2
				∫ ln(1 + x						)dx = ∫ x						−				+							−			+… dx =
																		2						3				4
				0							0
x3			x5		x7				x9					1				1									1					1				1
														2
=		−		+			−				+…				=							−								+					−		+…≈
	3		2 5		3	7		4		9							23		3					25			10				27		21			29 36
														0

≈ 241 − 3201 + 39681 −184321 +…≈ 241 − 3201 ≈ 0,039 .

Так как при вычислении интеграла мы получили знакочередующийся числовой ряд, то отбросив при вычислении его сумм все члены,

начиная с третьего члена 39681 , мы допустили ошибку, не превы-

шающую первого отброшенного члена (согласно признаку сходимо-

сти Лейбница). Поскольку же 39681 < 0,001, то наш интеграл вычис-

лен с точностью до 0,001.

112

Задача 12. Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения y′ = x2 + y2 , удовлетворяющего начальному условию y(0) =1.

Решение. Запишем искомое решение у(х) дифференциального уравнения в виде степенного ряда Маклорена

y(x) = y(0)+		y′(0)		x +	y′′(0)	x2	+… .	(9.23)
		1!	2!
Найдем последовательно		y(0), y′(0) и y′′(0). Из начального усло-
вия следует, что y(0) =1.	Непосредственно						из дифференциального
уравнения находим, что y′(0) = 02			+ y2 (0) =1.
Продифференцировав	обе			части			уравнения,	получим:
y′′= 2x + 2 y y′. Отсюда,	y′′(0) = 2 0 + 2 y(0) y′(0) = 2 1 1 = 2 . Под-

ставляя найденные значения производных в (9.23), получим искомое разложение

y(x) =1 + x + 22! x2 +…=1 + x + x2 +… .

113

Тема 10. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

10.1.Двойные интегралы, их вычисление

вдекартовой и полярной системах координат

Двойной интеграл определяется как конечный предел интегральной суммы от функции двух переменных z = f (x; y) по двумерной

области D и обозначается ∫∫ f (x; y)dxdy [2].

D

Если область D ограничена прямыми x = a, x = b (проектируется на ось Ox в отрезок [a; b]) и графиками функций y = ϕ1 (x) и y = ϕ2 (x) , причем ϕ2 (x) ≥ ϕ1 (x) при x [a;b], и любая прямая, параллельная оси

Oy, пересекает границу области не более чем в двух точках (рис. 10.1), то двойной интеграл вычисляется по формуле

	b	ϕ2 ( x)
∫∫ f (x; y)dxdy = ∫ dx		∫ f (x; y)dy .	(10.1)
D	a	ϕ1 ( x)

y

y = ϕ2 (x)

D

Стоящий в правой части (10.1) интеграл называется повторным интегралом и вычисляется следующим образом. Сначала вычисляют интеграл по переменной y от функции f (x; y) ,

						считая при этом, что x = const. Полу-
				y = ϕ1(x)
						чившуюся в результате новую функцию
			a			f1 (x) интегрируют	по переменной x
	O				b
						x
						и в итоге получают число, которое рав-
			Рис. 10.1			но искомому двойному интегралу.
	Если область D ограничена прямыми y = c,						y = d (проектируется
на ось			Oy	в отрезок		[c; d] ) и графиками	функций x = ψ1 ( y)

и x = ψ2 ( y) , причем ψ2 ( y) ≥ ψ1 ( y)	при y [c; d] , и любая прямая, па-
раллельная оси Oх пересекает границу области не более чем в двух
точках (рис. 10.2), то двойной интеграл вычисляется по формуле
	d	ψ2 ( y )
∫∫ f (x; y)dxdy = ∫ dy		∫ f (x; y)dx.	(10.2)
D	c	ψ1 ( y )
114

При этом сначала вычисляют интеграл по переменной x от функции f (x; y) , счи-

тая, что y = const , затем получившуюся функцию f2 ( y) интегрируют по переменной y и в результате получают число, котороеравноискомомудвойномуинтегралу.

	y
	d
				x = ψ2 (x)
		x = ψ (x)
		1

D

Задача 1. Вычислить двойной инте-

c

грал от функции

f (x; y) = x + y по облас-

O

x

ти D, ограниченной

прямыми x = 0,

y = x и y = 1.

Рис. 10.2

Решение. Изобразим область D (рис. 10.3, а).

y

y

1

y =1

1

D

D

x = 0

y = x

x = y

x

x

O

1

O

1

a

б

Рис. 10.3

Область D проектируется на ось Ox в отрезок [0;1]. В соответствии с формулой (9.1) получим:

						1			1									1							y2						1
∫∫(x + y)dxdy = ∫ dx∫(x + y)dy = ∫																				xy			+								dx =
																									2
D						0			x									0													x
1			12								x2							1 1							3x			2
= ∫ x 1 +						− x x −									dx = ∫						+ x −								dx =
			2								2														2
0																		0 2
		x x2								x3					1	1		1			1			1
	=					+		−								=		+			−		=			.
				2			2			2					0		2		2			2			2

115

Данный двойной интеграл можно вычислить и по формуле (10.2), Спроектировав область D на ось Oy в отрезок [0;1], как показано на

рис. 10.3, б. Тогда

		1	y	1	x2				y
	∫∫(x + y)dxdy = ∫ dy∫(x + y)dx = ∫						+ yx		dy =
						2
	D	0	0	0					0

1	y2			2		1	3y2		y2			1	1
= ∫			+ y		dy = ∫			dy =				=		.
		2					2		2				2
0						0						0

Замечание 1. Переход при вычислении двойного интеграла от расстановки пределов интегрирования по формуле (10.1) к расстановке пределов по формуле (10.2) называется изменением порядка интегри-

рования.

Замечание 2. Если область D не удовлетворяет вышеуказанным условиям, то ее разбивают на несколько областей, каждая из которых удовлетворяет указанным условиям.

В некоторых случаях вычисление двойного интеграла значительно упрощается, если перейти к полярной системе координат.

При переходе от декартовых координат x и y к полярным r		и ϕ по
формулам x = r cosϕ и	y = rsin ϕ двойной интеграл преобразуется
по формуле
∫∫ f (x; у)dxdy = ∫∫ f (r cos ϕ; r sin ϕ)rdrdϕ,		(10.3)
D	D

причем стоящий в правой части (10.3) интеграл также вычисляется сведением к повторному. Возможны следующие три случая.

1. Полюс находится вне области интегрирования. Область интегрирования D ограничена лучами ϕ = α и ϕ =β (α <β), граничными кривыми r = φ1 (ϕ) и r = φ 2 (ϕ), причем любой луч, выходящий из по-

люса и проходящий через область D, пересекает границу не более чем в двух точках (рис. 10.4). Тогда

	β	φ2	(ϕ)
∫∫ f (r cos ϕ; r sin ϕ)rdrdϕ = ∫ dϕ ∫ f (r cos ϕ; r sin ϕ)rdr . (10.4)
D	α	φ1	(ϕ)

2. Полюс находится на границе области, и область интегрирования D ограничена лучами ϕ = α и ϕ = β (α <β) (рис. 10.5). Тогда ин-

теграл (10.3) вычисляется по формуле

116

β

∫∫ f (r cos ϕ; r sin ϕ)rdrdϕ = ∫ dϕ

D

α

B

r = φ2 (ϕ)

D

φ(ϕ)
∫ f (r cos ϕ; r sin ϕ)rdr .	(10.5)
0

B

r = φ(ϕ)

	r = φ1(ϕ)	A	D
	α β		α β	A

O	r	O		r
Рис. 10.4			Рис. 10.5

3. Полюс находится внутри области интегрирования D (рис. 10.6), интеграл (9.3) вычисляется по формуле

∫∫ f (r cos ϕ; r sin ϕ)rdrdϕ =

D

r = φ(ϕ)

D

O r

2π φ(ϕ)

∫ dϕ ∫ f (r cos ϕ; r sin ϕ)rdr . (10.6)

0 0

y

3

D

O	3 x

Рис. 10.6

Рис. 10.7

Замечание. Если область D не удовлетворяет вышеуказанным условиям, то ее разбивают на несколько областей, каждая из которых удовлетворяет указанным условиям.

Задача 2. Вычислить ∫∫ x2 + y2 dxdy , где D – четверть круга ра-

D

диуса R = 3, лежащая в 1-м квадранте. Решение. Изобразим область D на рис. 10.7.

117

Границу области D и подынтегральную функцию удобнее выразить в полярных координатах, поэтому переходим к полярным координатам и вычисляем данный интеграл по формуле (10.4):

∫∫ x2 + y2 dxdy = ∫∫			r 2 cos2 ϕ + r 2 sin 2 ϕ rdrdϕ = ∫∫r 2 drdϕ =
D	D											D
π			π			3		3		π	9π
2	3		2							2
= ∫ dϕ∫ r		2		r								.
			dr = ∫		3				dϕ = ∫9dϕ =		2
0	0		0					0		0

Замечание. Свойства двойного интеграла аналогичны свойствам определенного интеграла. В частности, двойной интеграл по области D от функции, тождественно равной единице, равен площади области D:

∫∫1 dxdy = SD .	(10.7)
D

10.2.Тройные интегралы, их вычисление

вдекартовой и цилиндрической системах координат

Тройной интеграл определяется как конечный предел интегральной суммы от функции u = f (x; y; z) по трехмерной области V и обо-

значается ∫∫∫ f (x; y; z)dxdydz [2].

V

Если f (x; y; z) ≡1, то тройной интеграл равен объему области V . Вычисление тройного интеграла сводится к повторному, а затем

к последовательному вычислению трех определенных интегралов. Ес-
ли область V снизу ограничена поверхностью z = ψ1 (x; y),						сверху –
поверхностью z = ψ2 (x; y), а проекция этой области на плоскость xOy
есть область D, ограниченная прямыми				x = a, x = b	и графиками
функций y = ϕ1(x) и y = ϕ2 (x) , причем				ϕ2 (x) ≥ ϕ1 (x)	при	x [a; b]
(рис. 10.8), то тройной интеграл вычисляется по формуле
∫∫∫ f (x; y; z)dxdydz = ∫∫ dxdy			ψ2 (x, y )
				∫ f (x; y; z)dz =
V	D		ψ1 (x, y )			(10.8)
b	ϕ2 ( x) ψ2	(x, y )
= ∫ dx ∫ dy		∫ f (x; y; z)dz .
a	ϕ1 ( x) ψ1 (x, y )
118

В тройном интеграле сначала вычисляют интеграл по переменной z , считая x и y постоянны-

ми. Таким образом, тройной интеграл сводится к двойному, и затем можно интегрировать по переменной y , считая x постоян-

ной, и наконец, по переменной x . Получившееся число и есть искомый тройной интеграл.

z	z = ψ2 (x; y)

z = ψ1 (x; y)

O

		a					y
			y = ϕ1 (x)
					D
						y = ϕ2	(x)
b
	x			Рис.10.8

Задача 3. Вычислить ∫∫∫ xdxdydz , где V – область, ограниченная

V

плоскостями x = 1, y = 2x, z = 0 и x + y + z = 4 .

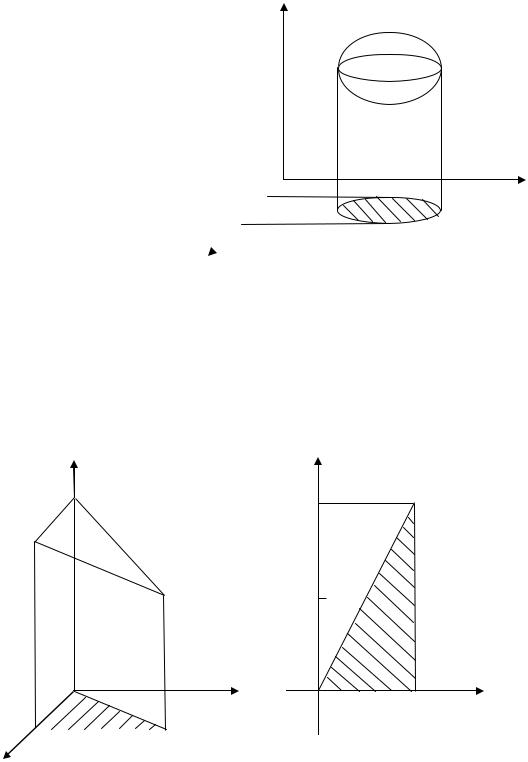
Решение. Область V – это усеченная призма, изображенная на рис. 10.9. Проекция этой призмы на плоскость xОy – это треугольник, изображенный на рис. 10.10.

z

y

4

2

z = 4 − x − y

1

y = 2x

D

O

y

x

D

y = 2x

O

1

1

x

Рис. 10.9

Рис. 10.10

В соответствии с формулой (10.8) получим:

119

z = x2 + y2

			1	2 x	4−x−y				1	2 x		(xz			04−x−y )dy =
∫∫∫ xdxdydz = ∫ dx ∫ dy						∫ xdz = ∫ dx ∫
V			0	0		0			0	0
1	2 x					1										y2				2 x
= ∫ dx ∫(x(4 − x) − xy)dy = ∫ x(4 − x)y − x																						dx =
																2
0	0					0														0
																						1
1		2		1	2			3		8x3								4					8				5
= ∫(x(4 − x)2x − x2x			)dx	= ∫(8x		−	4x		)dx =							− x						=			−1	=		.
												3											3				3
0				0																		0

В некоторых случаях вычисление тройного интеграла значительно упрощается, если от декартовой системы координат x; y; z перейти

кцилиндрическим координатам r; ϕ; z по формулам:

x= r cosϕ; y = r sin ϕ; z = z (0 ≤ r ≤ +∞, 0 ≤ ϕ≤ 2π, − ∞ < z < +∞) .(10.9)

Тройной интеграл преобразуется следующим образом:

∫∫∫ f (x; y; z)dxdydz = ∫∫∫ f (r cos ϕ; r sin ϕ; z)rdrdϕ dz . (10.10)

V V

Вычисление стоящего в правой части (10.10) интеграла осуществляется путем его преобразования к последовательному вычислению трех определенных интегралов.

Задача 4. Найти объем тела, ограниченного поверхностями z = x2 + y2 и z = 9 .

Решение. Изобразим тело, ограниченное эллиптическим параболоидом и плоскостью z = 9, перпендикулярной оси Оz

(рис. 10.11).

Проекция этого тела на плоскость xOy − это круг радиуса R = 3 (рис. 10.12), так как линией пересечения данных поверхностей является окружность x2 + y2 = 32 , лежащая в плоскости z = 9 .

Учитывая, что уравнение эллиптического параболоида в цилиндрических координатах имеет вид z = r 2 cos2 ϕ + r 2 sin 2 ϕ = r 2 , а уравнение окружности r = 3 , и полюс находится внутри области D, вычислим объем тела с помощью тройного интеграла в цилиндрических координатах:

										2 π	3	r	2	2 π	3
V = ∫∫∫1 dxdydz = ∫∫∫rdrdϕdz = ∫ dϕ∫ dr ∫ rdz =∫ dϕ∫ (r z																	0r	2	)dr =
	V		V							0	0	0		0	0				(10.11)
2 π	3	2 π		4			3		81	2 π		81		81π
	3	r
= ∫ dϕ∫ r		dr = ∫						dϕ =		∫ dϕ =			2π =		(куб. ед.).
			4						4			4		2
0	0	0					0			0

120