Волк_Высшая математика.2010

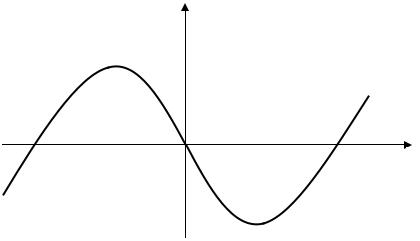
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. В этих точках изменяется направление вогнутости графика функции.

В точке перегиба M0 (x0 ; y0 ) вторая производная f ′′(x0 ) равна нулю или не существует.

Задача 4. Исследовать на выпуклость и вогнутость функцию f (x) = x3 −3x .

							′		2
	Решение.		Находим	вторую	производную:		f (x)	= 3x		−3,
	′′			′′		6x = 0 , откуда x = 0 . Видим,
	f (x) = 6x . Приравниваем f			(x) к нулю:
	что если	x < 0 ,	′′			x > 0 , то f	′′			за-
			то f (x) = 6x < 0 , а если				(x) = 6x > 0 ,
	ключаем,	что в интервале ( −∞;0)			график выпуклый, а в интервале
	(0;+∞) –	вогнутый. При		x =0	функция имеет		точку	перегиба
	(рис. 4.3).

y

O

x

Рис. 4.3

4.6.Общая схема исследования функции

ипостроения графика

При исследовании функций и построении их графиков полезно придерживаться следующей схемы:

1)найти область определения функции и интервалы непрерыв-

ности;

2)если есть точки разрыва, найти односторонние пределы функции в этих точках и изобразить на чертеже поведение функции в каждой точке разрыва;

61

3)исследовать функцию на четность и нечетность, периодич-

ность;

4)найти вертикальные, горизонтальные и наклонные асимптоты, если они есть;

5)найти интервалы монотонности функции и точки экстремума;

6)найти интервалы выпуклости и вогнутости графика функции, точки перегиба;

7)найти точки пересечения графика функции с координатными осями (если это возможно) и построить график с учетом полученных результатов.

Задача 5. Исследовать функцию	y =	x2
				и построить ее график.
		x2
			−1

Решение

1)Функция не определена при x1 = −1 и x2 =1, поэтому область определения функции D( y) = (−∞; −1) (−1;1) (1; +∞).

2)Так как в точках x1 =1 и x2 = −1 функция не определена, то это

точки разрыва функции. Исследуем поведение функции в окрестности этих точек. Для этого вычислим односторонние пределы:

y(1 + 0 ) =

lim

x2

=

lim

x2

=

1

=

1

= +∞.

x2 −1

( x +1)( x −1)

2

(1

+ 0

−1)

2

(+0)

x→1+0

x→1+0

Вычисленный односторонний предел оказался бесконечным, поэтому прямая x =1 будет вертикальной асимптотой графика функции.

y(1 − 0) = lim

x2

=

1

=

1

= −∞.

(x +1)(x −1)

2(1

− 0 −1)

2(−

0)

x→1−0

Вычислим односторонние пределы функции в точке x2 = −1:

y(−1 + 0) = lim

x2

=

1

=

1

= −∞;

(x +1)(x −1)

− 2(−1 + 0 +1)

− 2(+ 0)

x→−1+0

y(−1 − 0) = lim

x2

=

1

=

1

= +∞.

(x +1)(x −1)

− 2(−1 − 0 +1)

− 2(− 0)

x→−1−0

Односторонние пределы и в точке x = −1 оказались бесконечными, поэтому прямая x = −1 будет вертикальной асимптотой графика функции.

62

	3) Поскольку y(− x) =	(− x)2		=	x2		= y(x), то функция четная.
		(− x)2 −1			x2 −1

4) Так как односторонние пределы функции в точках x1 = −1 и x2 =1 равны бесконечности, то прямые x1 = −1 и x2 =1 будут вертикальными асимптотами графика функции.

Для нахождения наклонной асимптоты (4.1)

y = k x +b графика

функциивычислимдвапредела(4.3): k = lim

f

(x)

и b = lim( f (x)− k x):

x→ ∞

x

x→∞

k = lim

x2

∞

1

1

=

= lim

=

= 0 ;

(x

2

−1)

1

∞

x→∞ x

∞

x→∞

x 1

−

x

2

x2

x2

1

1

b = lim

−0 x = lim

= lim

=

=1.

2

−1

2

−1

1

1 −

0

x→∞ x

x→∞ x

x→∞

1 −

x2

Значит, прямая

y = 0 x +1,

т.

е.

y =1

–

это

горизонтальная

асимптота графика функции и при х→+∞, и при х→ – ∞.

5) Вычислим производную, найдем критические точки, интервалы монотонности и точки экстремума:

2

2x(x

2

−1)− x

2

x

′

2x

− 2x

y′ =

=

=

;

2

(x

2

2

−1

(x

2

2

x

−1)

−1)

y′ =

−2x

= 0 x =

0 .

(

)

2

x2 −1

В точках x1 = −1 и x2 =1 производная не существует.

Составим таблицу изменений знака производной y′ (табл. 4.1).

Таблица 4.1

x

(–∞; –1)

–1

(–1; 0)

0

(0; 1)

1

(1; + ∞)

y′

+

Не сущ.

+

0

–

Не сущ.

–

y

Возр.

Экстр.

Возр.

Макс.

Убыв.

Экстр.

Убыв.

ymax = 0

нет

нет

Так как

y′ > 0 при

x (− ∞;−1) (−1;0), то на этих интервалах

функция возрастает.

63

При x (0;1) (1; +∞) производная y′ < 0 , следовательно, на этих

интервалах функция убывает.

Поскольку y′(0) = 0 , то x = 0 – единственная критическая точка функции, а так как y′ меняет знак в точке 0 с « + » на « – », то x = 0 – точка максимума функции, причем y(0) = 0 .

6) Интервалы выпуклости и вогнутости найдем по знаку производ-

ной второго порядка

y′′. Найдем вторую производную и возможные

точки перегиба:

′

− 2x

1 (x2

−1)2 − x 2(x2 −1)2x

2(1 +3x2 )

y′′ =

= −2

=

.

(x2 −1)2

(x2 −1)4

(x

−1)3

2

В точках x1 = −1 и x2 =1 вторая производная не существует.

Составим таблицу изменений знака y′′ (табл. 4.2).

Таблица 4.2

х

(–∞; –1)

–1

(–1; 1)

1

(1; +∞)

y′′

+

Не сущ.

–

Не сущ.

+

у

(вогн.)

Не сущ.

∩ (выпукл.)

не сущ.

(вогн.)

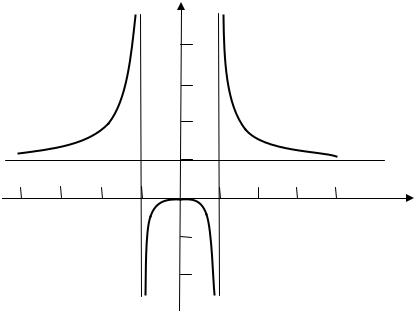
Итак, на интервалах (–∞; –1) и (1; +∞) график функции вогнутый,

ана интервале (–1; 1) – выпуклый. Точек перегиба нет.

7)Учитывая, что y(0) = 0, строим график (рис. 4.4).

y

4

3

2

1

0

–4

–3

–2

–1

1

2

3

4

x

−1

−2

Рис. 4.4

64

Задача 6. Исследовать функцию y = xe−x и построить ее график.

Решение

1)Область определения функции – вся числовая прямая, т. е.

D( y) = R .

2)Данная функция является элементарной функцией, определенной на всей числовой оси, значит, точек разрыва, а следовательно

ивертикальных асимптот нет.

3)Поскольку y(− x) ≠ y(x) и (− x) ≠ −y(x), то y(x) – ни чет-y

ная, ни нечетная функция.

4) Исследуем наличие наклонной асимптоты при x → +∞. Так как

k = lim

f ( x)

=

lim xe−x

=

lim

1

=

1

= 0 ;

x

x→+∞

x

x→+∞

x

x→+∞

e

+∞

b = lim

( f ( x)

− k x) = lim

x

∞

x′

1

1

=

=

lim

=

lim

=

= 0 ,

x

(ex )′

x

x→+∞

x→+∞ e

∞

x→+∞

x→+∞ e

+∞

то прямая у = 0 – горизонтальная асимптота графика функции при

x → +∞ (являющаяся частным				случаем наклонной						асимптоты при
x → +∞).
Исследуем наличие наклонной асимптоты при x → −∞. Так как
k = lim		f ( x)	= lim	xe−x		= lim	1	= e+∞ = +∞,
		x		x
x→−∞			x→−∞			x→−∞ ex
то при x → −∞ наклонной асимптоты нет.
5) Вычислим производную, найдем критические точки, интер-
валы монотонности и точки экстремума:
	y′ = (xe−x )′ =1 e−x − x e−x = (1− x)e−x ;
		y′ = (1 − x)e−x = 0 x =1.
Составим таблицу изменений знака производной y′ (табл. 4.3).
										Таблица 4.3
x		(–∞; –1)				1				(1; +∞)
у′		+				0				–
y		Возр.				Макс.				Убыв.
						ymax = e−1
										65

Так как y′ > 0 при x <1 и y′ < 0 при x >1, то функция при x <1 возрастает, а при x >1 убывает. Так как y′(1) = 0 , то x =1 – един-

ственная критическая точка функции. Поскольку в критической точке функция меняет знак с « + » на « – », то x =1 – точка максимума

функции и y(1) = e−1 = 1e .

6) Интервалы выпуклости и вогнутости найдем по знаку производной второго порядка y′′. Найдем вторую производную и возмож-

ные точки перегиба:

y′′ = ((1− x) e−x )′ = −e−x −(1− x) e−x = (x −2) e−x ; y′′ = (x − 2) = 0 x = 2 .

Составим таблицу изменений знака у′′ (табл. 4.4).

			Таблица 4.4
х	(–∞; 2)	2	(2; + ∞)
у′′	–	0	+
у	∩ (выпукл.)	2 e−2	(вогн.)

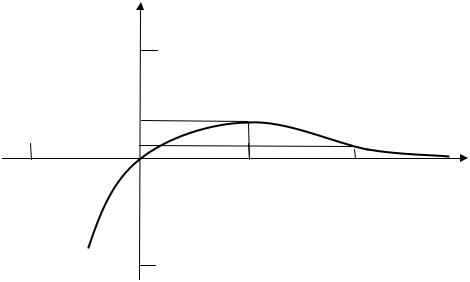
Так как y′′ > 0 при x > 2 и y′′ < 0 при x < 2 , то при x > 2 график функции вогнутый, а при x < 0 – выпуклый. Так как в точке x = 2 y′′ меняет знак, то точка M (2; 2a−2 ) – точка перегиба графика функции.

7) Учитывая, что y(0) = 0 , строим график функции (рис. 4.5).

y

	1
	e−1
					M
	e−2
−1	0		1	2		x

−1

Рис. 4.5

66

Тема 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

5.1. Первообразная и неопределенный интеграл

Определение. Функция F(x) называется первообразной для заданной функции f (x), если F′(x) = f (x).

Определение. Множество всех первообразных для функции f (x) называется неопределенным интегралом от функции f (x) и обозначается ∫ f ( x)dx .

Итак, если F ′(x) = f (x), то
∫ f (x) dx = F(x) + C .	(5.1)

При вычислении неопределенных интегралов используют свойства интегралов, таблицу неопределенных интегралов, различные методы интегрирования, а также тождественные преобразования подынтегральной функции.

Свойства неопределенных интегралов

1.∫ dF(x) = F(x)+C.

2.∫( f ( x) ± g ( x))dx = ∫ f ( x)dx ± ∫ g ( x)dx.

3.	∫ kf (x)dx = k ∫ f (x)dx, где k = const.
4.	∫ f (ax + b)dx =	1F(ax + b) + C .
		a

Таблица неопределенных интегралов

xα+1

1. ∫ xαdx = α +1 +C, (n ≠ −1). 2. ∫ dxx = ln x +C.

3. ∫ ex dx = ex +C.

4. ∫ ax dx = ax + C. lna

5.∫sin xdx = −cos x + C.

6.∫ cos xdx = sin x +C.

67

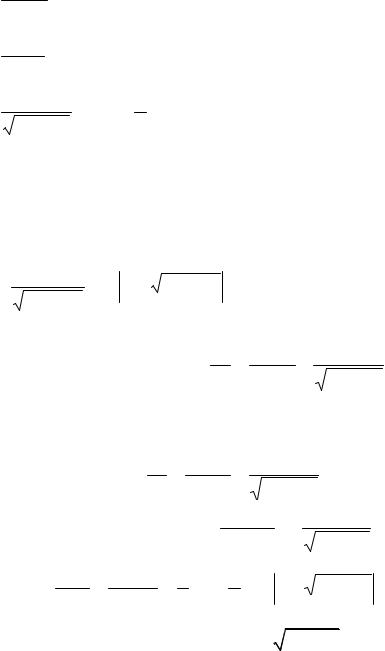
7.∫ cosdx2 x = tgx + C.

8.∫ sindx2 x = −ctgx + C.

9. ∫

dx

= arcsin

x

+ C.

a

2

− x

2

a

10 ∫

dx

=

1 arctg

x

+ C.

a

2

2

a

+ x

a

11. ∫

dx

=

1

ln

x − a

+ C.

x

2

2

2a

x + a

− a

12. ∫

dx

= ln x +

x2

± a 2

+ C.

x2

± a 2

3

1

2

1

−

+

2

−

2

Задача 1. Вычислить ∫ 4x

x

2

+ x

dx .

9

25 + x

Решение. Используя свойства и таблицу неопределенных интегралов, получим:

4x3 − 1

+

2

−

1

∫

2

2

dx =

x

2

9 + x

25 + x

3

dx −∫ x

−2

dx

+2∫

dx

− ∫

dx

=

= 4∫ x

3

2

+ x

2

5

2

+ x

2

= 4

x3+1

−

− 2 +1

+ 2arctg x

− ln x +

25 + x2

+ C =

3 +1

x−2+1

3

3

1 +

2 arc tg

x

= x4 +

−ln

x +

25 + x2

+ C .

x

3

3

5.2. Вычисление неопределенного интеграла методом замены переменной

Во многих случаях удается введением вместо переменной интегрирования x новой переменной t свести данный интеграл ∫ f (x)dx к новому интегралу, который или содержится в таблице основных

68

интегралов, или легко вычисляется другим способом. Этот метод интегрирования получил название метода замены переменной, или

интегрирование подстановкой.

Введем вместо x новую переменную t, связанную с х соотношением x = ϕ(t), где ϕ(t ) – непрерывная монотонная функция, имеющая не-

прерывную производнуюϕ′(t). Тогда имеет место формула

′	(5.2)
∫ f (x)dx = ∫ f (ϕ(t))ϕ (t)dt ,

которая называется формулой замены переменной (интегрирование подстановкой).

Задача 2. Вычислить ∫ 1 − x2 dx .

Решение. Сделав замену переменной x = sin t и учитывая, что

1 − x2 = 1 −sin 2 t = cos t,				dx = d(sin t) = costdt, получим:
	∫ 1 − x2 dx =∫cos2 tdt =			1 ∫	(1 + cos 2t)dt = 1		∫ dt +	1 ∫cos 2t(d
				2	2			2
	=	2t + sin 2t	+ C =			2arcsin x + sin(2arcsin x)			+ C =
	4				4
=	2arcsin x + 2sin(arcsin x) cos(arcsin x) + C = arcsin x + x 1 −
	4							2
	Задача 3. Вычислить ∫ex2 +1 xdx .
	Решение. Полагая t = x2				+1 и учитывая, что dt = 2xdx и

получим:
∫ex2 +1 xdx = ∫et dt	= et	+ C =	1ex2 +1	+ C .
2	2		2

2t) =

x2 + C .

xdx = dt2 ,

5.3.Вычисление неопределенного интеграла методом интегрирования по частям

Вычисление интеграла по формуле

∫udv = uv − ∫vdu (5.3)

называется интегрированием по частям.

69

Этой формулой пользуются в том случае, когда интеграл ∫ vdu

более простой, чем ∫ udv . Укажем некоторые часто встречающиеся

интегралы, которые вычисляются методом интегрирования по частям. 1. Интегралы вида

∫ Pn (x) eαx dx ;

∫Pn (x)sin αxdx ;

∫Pn (x)cos αxdx ,

где Pn (x) – многочлен n-й степени, а α некоторое число. Интегралы этих типов берутся по частям, если принять u = Pn (x), а оставшуюся часть за dv .

Задача 4. Вычислить ∫ ( x 2 + 1)	e3 x dx .
Решение. Положим u = x2 +1 и dv = e3xdx .
Тогда du = (x2 +1)′dx = 2x dx ,	v = ∫e3xdx =	1 e3x . Применяя фор-
		3

мулу интегрирования по частям, получим:

∫(x2 +1) e3 x dx = 13 (x2 +1)e3 x − 23 ∫ xe3 x dx + C .

Снова полагая u = x и dv = e3xdx , т. е. du = dx, v = 13 e3x , по-

лучим:

∫ xe3xdx = 13 xe3x − 13 ∫e3x dx = 13 xe3x − 19 e3x + C.

Итак, окончательно имеем:

∫(x2 +1) e3 x dx = 1	(x2	+1)e3 x −		2	1 xe3 x			−	1 e3 x	+ C =
3				3	3				9
= e3 x	x2	+1 −	2x	+	2		+ C.
3			3		9

2. Интегралы вида

∫ Pn (x) arcsin xdx ;

70