Волк_Высшая математика.2010

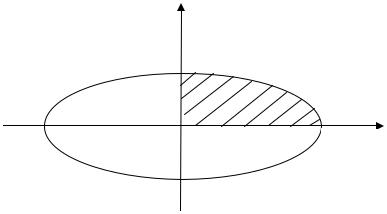
Задача 5. Найти площадь фигуры, ограниченной кривой x = acost ,

y = bsint , 0 ≤ t ≤ 2π.
Решение. Так как
	x2	+	y2		= a2 cos2 t	+ b2 sin 2 t	= cos2 t + sin 2 t =1,
	a2		b2
					a2	b2

то данные параметрические уравнения описывают эллипс. Вычислим площадь S1 части эллипса, расположенной в первой четверти

(рис. 6.5), по формуле (6.6):

S1	= ∫bsin t (a cost)′dt = −ab∫sin 2													π
											tdt = ab ∫2 (1 − cos 2t)dt =
	0								0
	π								π				2 0
	2								2
= ab		t −	1 sin2t			π	= ab	π		1 sinπ−0			+ 1 sin0				πab .
						2			−							=
	2		2			0	2	2		2			2				4

Отсюда площадь всего эллипса S = 4S1 = πab (кв. ед.).

y

b

O

a

x

Рис. 6.5

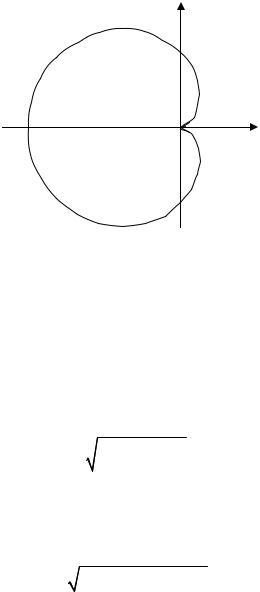
Задача 6. Найти площадь фигуры, ограниченной кривой r =1 − cos ϕ.

Решение. Данная линия является кардиоидой (рис. 6.6), функция r(ϕ) определена при всех значениях аргумента, имеет период 2π.

Искомую площадь вычислим по формуле (6.7):

81

		S =		1 2∫π(1 −cos ϕ)2 dϕ =				1 2∫π(1 − 2 cos ϕ+ cos2 ϕ)dϕ =
				2 0				2 0
=	1	2π 1 − 2cos ϕ+			1 + cos 2ϕ		dϕ =1				2π 3	− 2cosϕ+ 1 cos 2ϕ dϕ =
	2
		∫0			2			2			∫0 2		2
		= 1		3 ϕ− 2sin ϕ+		1 sin 2ϕ				2π = 3 2π			= 3π (кв. ед.),
		2		2		4				0		4	2

так как sin 2πn = 0 , n Z .

y

a

O x

Рис. 6.6

6.4. Применение определенного интеграла для вычисления длин дуг плоских кривых

Длина	L	кривой,	являющейся	графиком функции	y = f (x),
a ≤ x ≤ b , вычисляется по формуле
			b	( x))2 dx .
			L = ∫ 1 +( f ′		(6.8)
			a
Длина	L	кривой,	заданной параметрическими уравнениями
x = ϕ(t ) , y = ψ(t), α ≤ t ≤β, вычисляется по формуле
			β
		L = ∫ (ϕ′(t))2 + (ψ′(t))2 dt .			(6.9)

α

82

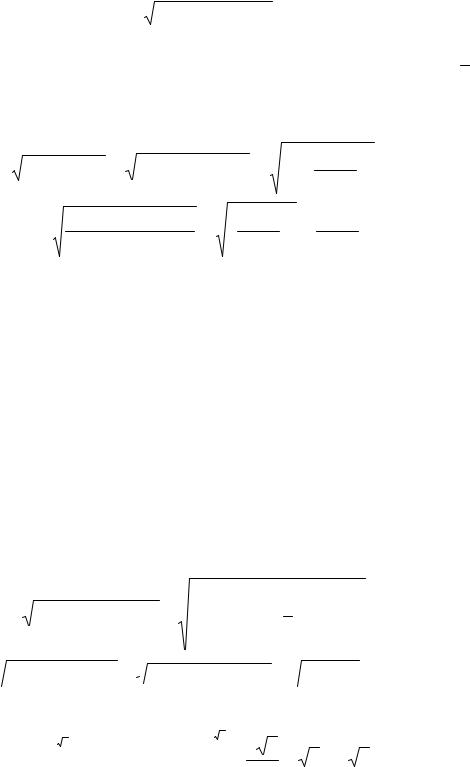
Длина L кривой, заданной в полярных координатах уравнением r = r(ϕ), α ≤ ϕ ≤β, вычисляется по формуле

β
L = ∫ r 2 (ϕ) + (r′(ϕ))2 dϕ.	(6.10)

α

Задача7. Вычислитьдлинудугикривой y = ln(1 − x2 ), если 0 ≤ x ≤ 12 .

Решение. Используем формулу (6.8), преобразовав предварительно подынтегральную функцию:

1 + ( f ′(x))2 = 1 + (ln′(1 − x2 ))2 = 1 + − 2x								2	=
						1 − x2
=	1 − 2x2	+ x4 + 4x2	=	1 + x2	2	=	1 + x2	.
	(1	2					1 − x2
		− x2 )		1 − x2

Поэтому

	1		1 + x2					1					x2 −1 + 2											1								2
2							2																	2
L = ∫					dx = −∫															dx = −∫						1			+							dx =
			1 − x	2												x	2	−1													x	2
0							0																	0									−1
							x −1								1							1		−1
															2				1				2														1
= − x + ln																= −				+ ln										= ln 3					−				.
							x +1												2			1															2
															0									+1
																						2
Задача 8. Вычислить длину дуги кривой x = t2 ,																																		y =				t	(t2 −3).
																																					3
Решение. Так как кривая задана параметрическими уравнениями,

то используем формулу (6.9), преобразовав предварительно подынтегральную функцию:

2 ′

2

1 3

′ 2

′

2

′

2

(t

)

+

t

− t

=

(ϕ (t))

+ (ψ (t)) =

3

= (2t)2 + (t 2 −1)2 = 4t 2 + t 4 − 2t 2 +1 = (t 2 +1)2 = t 2 +1.

Находим пределы интегрирования из условия у = 0 и получаем:

3		2	t3				3	3 3
L = ∫	(t		+1)dt =		+ t		=		+ 3	= 2 3 .
				3				3
0							0

83

6.5. Применение определенного интеграла для вычисления объемов тел вращения

Объем тела, образованного вращением вокруг оси Оx криволинейной трапеции, ограниченной кривой y = f (x) , осью Оx и двумя

прямыми x = a и x = b (рис. 6.7), вычисляется по формуле

b	(x)dx .
Vx = π∫ y2		(6.11)

a

Аналогично объем тела, образованного вращением вокруг оси Оy криволинейной трапеции, ограниченной кривой x = g(y) , осью

Оy и двумя прямыми y = c и y = d (рис. 6.8), вычисляется по формуле

d

( y)dy .

Vy = π∫ x2

(6.12)

c

y

y

y = f (x)

d

O a

b

x = g(y)

x

c

O

x

Рис. 6.7

Рис. 6.8

Задача9. Вывестиформулудлявычисленияобъемашарарадиуса R .

Решение. Поскольку объем шара радиуса

R равен объему тела

вращения окружности

x2 + y2

= R2

вокруг оси

Оx ,

то по формуле

(6.11) получим:

R

2

2

2

x3

R

4

3

V = ∫

(R

− x

)dx = π R

x −

=

πR

(куб. ед.).

−R

3

−R

3

84

6.6. Несобственные интегралы

Пусть функция f ( x) непрерывна на промежутке [a; + ∞) , тогда она интегрируема на любом отрезке [a; b], где a < b < +∞.

Определение. Несобственным интегралом функции f ( x) по бесконечному промежутку [a; +∞) называется предел, определяемый равенством

+∞		(		)	b		(		)
∫	f		x		b→+∞ ∫	f		x		dx .	(6.13)
					dx = lim
a					a

Если этот предел существует и является конечным, то несобственный интеграл (6.13) называется сходящимся, если же предел не существует или равен бесконечности – расходящимися.

Аналогично определяются несобственные интегралы по бесконечным промежуткам (−∞; a] и ( −∞; +∞) :

b

(

)

b

(

)

∫

f

x

dx

a→−∞ ∫

f

x

dx ,

(6.14)

= lim

−∞

a

+∞

(

)

c

(

)

b

(

)

∫

f

x

a→−∞ ∫

f

x

b→+∞ ∫

f

x

dx .

(6.15)

dx = lim

dx + lim

−∞

a

c

Пусть функция f (x) непрерывна на промежутке [ a; b ] и не ограничена при x = b , тогда несобственный интеграл от неограниченной функции f ( x) на отрезке [ a; b ] определяется равенством

b		b−ε
∫ f ( x)dx =	ε→+lim0	∫	f ( x)dx .	(6.16)
a		a

Если этот предел существует и является конечным, то несобственный интеграл (6.16) называется сходящимся, если же предел не существует или равен бесконечности – расходящимся.

Аналогично определяются несобственные интегралы от функций с бесконечными разрывами в точках a и c , если a < c < b.

+∞ dx

Задача 10. Вычислить несобственный интеграл ∫0 1 + x2 (или до-

казать его расходимость).

85

Решение. Используем формулу (6.13):

	+∞	dx			b	dx			(arctg x		b0 ) =
	∫			= lim	∫			= lim
		1 + x	2			1 + x	2
				b→+∞				b→+∞
	0				0

= lim (arctgb −arctg 0) = π −0 = π .

b→+∞ 2 2

Итак, несобственный интеграл сходится и равен π2 .

1

dx

Задача 11. Вычислить несобственный интеграл ∫0

(или до-

(x −1)2

казать его расходимость).

1

Решение.

Так

как

подынтегральная

функция

f (x) =

(x −1)2

не ограничена при x →1 −0 , то используем формулу (6.15):

1

dx

1−ε

d(x −1)

1−ε

−1 =

= lim

= lim

−1

= lim

−1

−1

−1 = +∞.

0

( x −1)

2

0 ( x

−1)

2

1 −ε −

1

−0

ε→+0

x −1

0

∫

∫

ε→+0

ε→+0

Итак, несобственный интеграл расходится.

86

Тема 7. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

7.1. Общие понятия. Обыкновенные дифференциальные уравнения 1-го порядка. Решение дифференциальных уравнений с разделяющимися переменными, однородных и линейных

Определение. Дифференциальным уравнением называется урав-

нение, связывающее независимую переменную х с искомой функцией y(x) и ее производными, записывается в виде

′ ′′	(n )	)= 0 .	(7.1)
F(x; y; y ; y ; …; y

Определение. Порядком дифференциального уравнения называется наивысший порядок производной, существенно входящей в уравнение.

Уравнение (7.1) – дифференциальное уравнение n-го порядка. Определение. Решением или интегралом дифференциального

уравнения называется всякая функция, которая будучи подставленной в уравнение обращает его в тождество.

Дифференциальное уравнение первого порядка в общем случае записывается в виде

F(x; y; y′) = 0.

(7.2)

Если дифференциальное уравнение (7.2) можно разрешить относительно y′, то оно называется обыкновенным дифференциальным уравнением 1-го порядка, разрешенным относительно производной и записывается

y′ = f (x; y) .			(7.3)
Задача, в которой требуется найти решение дифференциального
уравнения (7.3), удовлетворяющее начальному условию
y		x= x0 = y0 ,	(7.4)

называется задачей Коши.

Определение. Общим решением дифференциального уравнения 1-го порядка называется функция y = ϕ(x; c) , зависящая от аргумен-

та х и произвольной постоянной c и удовлетворяющая следующим двум условиям:

87

1)при любом значении произвольной постоянной с она обращает уравнение в тождество;

2)для любых начальных условий (7.4) существует единственное

значение произвольной постоянной c = c0 такое, что решение y = ϕ(x; c0 ) удовлетворяет данному начальному условию.

Определение. Решение, полученное из общего решения при конкретном значении c = c0 , называется частным решением дифференци-

ального уравнения.

Рассмотрим решение некоторых типов дифференциальных уравнений 1-го порядка.

Дифференциальное уравнение вида

	dy	= f (x) f	2	(y)	(7.5)
	dx	1
называется уравнением с разделяющимися					переменными. Если

f2 ( y) ≠ 0 , то, разделив переменные в (7.5) и проинтегрировав обе части

равенства, получим общее решение:
	dy		= f1 (x) dx ,	∫	dy		=	∫	f1 (x) dx + c .
	f2 (y)				f2 (y)

Задача 1. Решить уравнение y′ = xy .

Решение. Разделив переменные в уравнении dydx = xy , получим

dyy = dxx . Поэтому ∫ dyy = ∫ dxx +ln c , т. е. ln y = ln x + ln c , ln y = ln cx .

Итак, y = cx – искомое общее решение. Решение y = 0 получается из формулы общего решения при c = 0 .

Если правая часть уравнения				(7.3) представима	в виде
y
f (x; y) = ϕ		, то уравнение
x
		y
		y′ = ϕ			(7.6)
		x

называется однородным уравнением 1-го порядка. Для решения этого уравнения вводят новую функцию u(x) = y(xx) .

88

Тогда y = u x , y	′	′
		= u x + u , и уравнение (7.6) принимает вид

u′x + u = f (u). Разделяя переменные в этом уравнении, последовательно получим:

x dy = f (u) − u ; ∫

du

= ∫ dx

+ c .

f (u) − u

dx

x

Перейдя после интегрирования к функции

y(x) , получим общее

решение исходного уравнения.

Задача 2. Решить уравнение xy′ = y ln

y

.

x

Решение. Разделив обе части исходного уравнения на х, полу-

чим, y′ =

y

ln

y

.

Так как

это однородное

уравнение, то введем

x

x

y

Тогда y

′

′

функцию

u = x

.

и исходное уравнение примет

= u x + u ,

′

du

du

dx

вид u x + u

= u lnu , откуда

x dx = u(ln u −1),

=

x .

u(ln u −1)

Проинтегрировав обе части последнего соотношения, получим:

∫

dx

c

= ∫

du

; ln

x

+ ln

c

= ∫

d(ln u)

+ ln

;

x

u(ln u −1)

ln u −1

ln

cx

= ∫ d(ln u −1) = ln

ln u −1

.

ln u −1

y

Итак, cx = lnu −1, ln u = cx +1, u = ecx+1 ,

= ecx+1 .

x

Отсюда получаем y = x ecx+1 – общее решение уравнения.

Дифференциальное уравнение вида

y′ + p(x) y = q(x) ,

(7.7)

где p(x) и q(x)

– непрерывные функции от переменной x, называется

линейным уравнением 1-го порядка.

y(x) = u(x) v(x) . Тогда

Решение этого уравнения ищут в виде

y′ = u′v + uv′

и

(7.7) преобразуется

в

u′v + uv′ + p(x) uv = q(x) , или

u′v + u(v′ + p(x)v) = q(x) . Функцию v(x)

находят из условия

v′ + p(x)v = 0 .

(7.8)

89

После чего, решая уравнение
u′v = q(x) ,	(7.9)

находят функцию u(x) .

Таким образом, решение линейного дифференциального уравнения 1-го порядка (7.7) сводится к решению двух уравнений (7.8) и (7.9) с разделяющимися переменными.

Замечание. При решении уравнения (7.8) произвольную постоянную с полагают равной нулю, находят частное решение.

Задача 3. Найти частное решение уравнения y′ + 2xy = xe−x2 , удов-

летворяющее начальному решению y(0) =1.

Решение. Решение данного линейного дифференциального урав-

нения будем искать в виде

y(x) = u(x) v(x). Так как y

′

′

′

, то

= u v

+ uv

′

+ u(v

′

+ 2xv) = xe

−x2

.

получим u v

Найдем v(x)

из условия

v′ + 2xv = 0

(уравнение (7.8)). Имеем

dv = −2xv ,

∫ dv = −∫ 2xdx,

ln

v

= −x2 , v(x) = e−x2 .

dx

v

Далее найдем u ( x) из условия u′ e−x2

= x e −x2 (уравнение (7.9)).

Получим u′ = x , du = xdx , u = ∫ xdx + c , т. е.

u ( x) =

x2

+ c .

− x2

2

2

x

2

– общее решение исходного

Следовательно, y(x) =

2

+ c e

x = 0 и

y(0) =1, получим:

уравнения. Подставляя в общее решение

x2

−

x2

1 = (0 + c) 1, т. е. c =1. Следовательно, y(x) =

+1 e

2 – искомое

2

частное решение уравнения.

7.2. Решение дифференциальных уравнений 2-го порядка, допускающих понижение порядка

Дифференциальное уравнение называется уравнением, допускающим понижение порядка, если путем введения новой переменной, его можно свести к уравнению более низкого порядка.

Дифференциальное уравнение 2-го порядка в общем случае записывается в виде

90