Волк_Высшая математика.2010

Определение. Смешанным произведением трех векторов a , b

и c называется число, равное векторному произведению a ×b , умно-

женному скалярно на вектор c , и обозначается abc .

Для векторов, записанных в координатной форме, смешанное

произведение вычисляется по формуле

x1

y1

z1

abc =

x2

y2

z2

.

(1.17)

x3

y3

z3

Из определения скалярного

произведения

a b =

a

b

cosϕ и

формулы (1.15) можно найти косинус угла ϕ между векторами a и b :

cosϕ =	ab	=		x1x2 + y1 y2 + z1z2							(1.18)
	a b		x12 + y12 + z12 x22 + y22 + z22 .
Поскольку площадь параллелограмма, построенного на векторах
a и b , равна
		a ×b		=		a			b	sin ϕ,	(1.19)

то площадь S треугольника, построенного на векторах a и b , вычисляется по формуле

S =	1		a ×b		.	(1.20)
	2

Наконец, из определения смешанного произведения векторов a ,

b и c вытекает, что объем треугольной пирамиды, построенной на этих векторах, определяется формулой

V =	1		abc		.	(1.21)
	6

1.3. Основные сведения из аналитической геометрии

Общее уравнение прямой на плоскости в декартовой системе координат имеет вид

Ax + By + C = 0 .

(1.22)

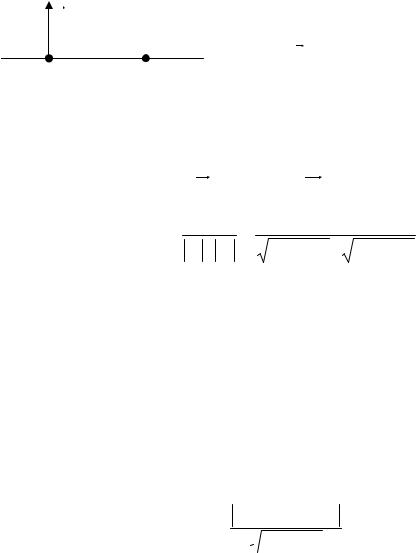
Вектор n ={A; B} называется нормальным вектором прямой. Он перпендикулярен прямой (рис. 1.4).

21

	n		Уравнение прямой, проходящей че-
			рез точку M 0 (x0 ; y0 ) перпендикулярно
			вектору n ={A; B}, имеет вид
	М0(х0; у0)		М(х; у)
			A(x − x0 )+ B(y − y0 ) = 0 . (1.23)
	Рис. 1.4

Если две прямые заданы уравнениями А1х + В1у + С1 = 0 и А2х +

+ В2у + С2 = 0, то угол ϕ между ними определяется как угол между их
нормальными векторами n1 ={A1; B1} и n2 ={A2 ; B2 }:
cosϕ = n1 n2 =		A2		A1 A2 + B1 B2			.	(1.24)
n1 n2				+ B2		A2	+ B2
		1		1		2	2
Следовательно, условие перпендикулярности двух прямых cosϕ = 0
или
A1 A2 + B1 B2 = 0 ,								(1.25)
а условие параллельности имеет вид
	A1	=	B1		.			(1.26)
	A
			B
2				2
Расстояние от точки M0 (x0 ; y0 )				до прямой (1.22) вычисляется по
формуле

d = Ax0 + By0 +C .

A2 + B2

Рассмотрим другие виды уравнений прямой на плоскости. Уравнение прямой, проходящей через заданную точку M 0 (x0 ; y0 )

параллельно вектору s ={m; n}, имеет вид

x − x0	=	y − y0	.	(1.27)
m
		n

Вектор s ={m; n} называется направляющим вектором прямой.

Уравнение прямой, проходящей через две точки M1(x1; y1) и M2 (x2 ; y2 ) , записывается по формуле

x − x1			=	y − y1			.	(1.28)
x	2	− x		y	2	− y
		1				1

22

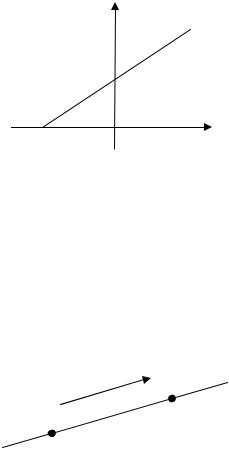
Угловым коэффициентом прямой называется тангенс угла α на-

клона прямой к оси Ох (рис. 1.5). Уравнение прямой с угловым коэффициентом k имеет вид

y = k x +b .

(1.29)

y

b

α

0	x

Рис. 1.5

а условие параллельности:

Уравнение прямой с угловым коэффициентом k, проходящей через заданную точку M0 (x0 ; y0 ) , записывается по

формуле

y − y0 = k(x − x0 ).

(1.30)

Если две прямые заданы уравнениями y = k1x + b1 и y = k2 x +b2 , то условие перпендикулярностиэтихпрямыхимеетвид

k1 k2 = −1,	(1.31)
k1 = k2.	(1.32)

Рассмотрим далее различные виды прямой в пространстве. Каноническое уравнение прямой в пространстве (рис. 1.6) имеет вид

s

x − x0

=

y − y0

=

z − z0

, (1.33)

M (x; y; z)

m

n

p

где

M

0

(x

;

y

; z

0

) –

точка, лежащая на

M0 (x0 ; y0 ; z0 )

0

0

прямой, а s ={m; n; p} – направляющий

Рис. 1.6

векторпрямой.

Уравнение прямой в пространстве, проходящей через две точки

M1(x1; y1; z1) и M2 (x2 ; y2 ; z2 )

записывается по формуле

x − x1

=

y − y1

=

z − z1

.

(1.34)

x

2

− x

y

2

− y

z

2

− z

1

1

1

Параметрическое уравнение прямой в пространстве имеет вид

x = x0 + mt,

y = y0 + nt,

− ∞ < t < +∞.

(1.35)

z = z0 + pt,

23

Общее уравнение плоскости в декартовой системе координат имеет вид

	Ax + By +Cz + D = 0 .	(1.36)
	Вектор	n ={A; B;C} называ-
n
	ется нормальным вектором плос-

		•	кости. Он перпендикулярен плос-
	M (x; y; z)		кости (рис. 1.7). Уравнение плос-
			кости, проходящей через точку
	M0 (x0 ; y0 ; z0 )
			M0 (x0 ; y0 ; z0 ) перпендикулярно
	Рис. 1.7		вектору n ={A; B;C}, имеет вид
	A(x − x0 )+ B(y − y0 )+C(z − z0 ) = 0 .			(1.37)
Уравнение плоскости,			проходящей через три точки M1(x1; y1; z1) ,

M2 (x2 ; y2 ; z2 ) и M3 (x3; y3; z3 ) , записывается по формуле

x − x1 x2 − x1 x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 . (1.38) z3 − z1

Если две плоскости заданы уравнениями А1х + В1у + С1z + D1= 0 и А2х + В2у + С2z + D2 = 0, то угол ϕ между ними определяется как угол между их нормальными векторами n1 ={A1; B1;C1} и n2 ={A2 ; B2 ;C2 }:

cosϕ = n1

n2

=

A1 A2 + B1 B2 + C1C2

.

(1.39)

n1

n2

A2 + B2 + C 2

A2

+ B2

+ C 2

1

1

1

2

2

2

Следовательно, условие перпендикулярности двух прямых имеет

вид cosϕ = 0 или

A1 A2 + B1B2 +С1С2 = 0 ,

(1.40)

а условие параллельности:

A1

=

B1

= C1 .

(1.41)

A

B

C

2

2

2

Расстояние от точки M0 (x0 ; y0 ; z0 ) до прямой (1.36) вычисляется по формуле

24

d = Ax0 + By0 +Cz0 + D .	(1.42)
A2 + B2 +C2

Рассмотрим кривые второго порядка.

Линии, задаваемые уравнением второй степени относительно текущих координат х и у, называются кривыми второго порядка. Простейшей кривой второго порядка является окружность.

y

0

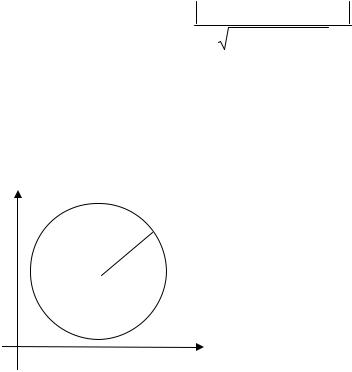
Определение. Окружностью

M (x; y) называется геометрическое место

Rточек плоскости, равноудаленных от данной точки этой плоскости,

•называемой центром окружности

M 0 (x0 ; y0 )	(рис. 1.8).
	Уравнение окружности радиу-
x	са R с центром в точке M 0 (x; y0 )
	имеет вид
Рис. 1.8	(x − x0 )2 + (y − y0 )2 = R2 . (1.43)

Уравнение окружности радиуса R с центром в начале координат записывается формулой

x2 + y2 = R2 .

(1.44)

Параметрическое уравнение окружности радиуса R с центром в начале координат имеет вид

x = R cost,	0 ≤t ≤ 2π.	(1.45)
y = Rsin t,

Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек этой плоскости (фокусов эллипса F1 и F2 ) есть величина постоянная (большая, чем расстояние между фокусами).

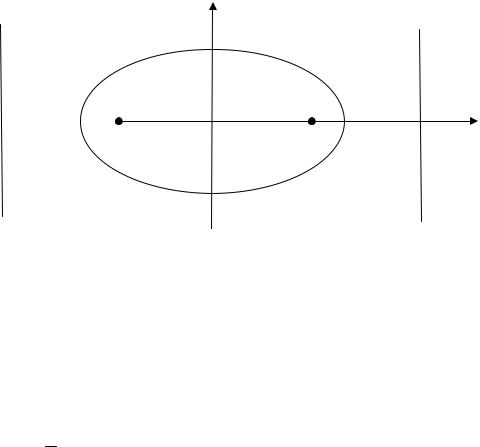
Если оси координат по отношению к эллипсу расположить так, как указано на рис. 1.9, то каноническое уравнение эллипса будет представлено следующим выражением:

	x2	+	y2	= 1.	(1.46)
	a2		b2
					25

y

B2 (0; b)

−a

x =

x =

a

ε

ε

A2 (a; 0)

A1 (−a; 0)

0

F1 (−c; 0)

F2 (c; 0)

x

B1 (0; −b)

Рис. 1.9

Точки пересечения эллипса с осями координат называются вер-

шинами эллипса. Вершины эллипса имеют координаты

А1

(− а; 0 ),

А2 (а; 0 ), B1 (0; −b),

B2 (0; b). Числа a и b называются соответственно

большей и малой полуосями эллипса. Расстояние между фокусами эллипса обозначим через 2с, тогда полуфокусное расстояние с связано

с полуосями соотношением a2 −b2 = c2 .

Число ε = aс , где а – большая полуось, называется эксцентриси-

тетом эллипса. Эксцентриситет характеризует вытянутость эллипса вдоль большей полуоси. Чем больше эксцентриситет, тем больше вытянутый эллипс. Для эллипса 0 < ε <1 (для окружности ε = 0 ).

Две прямые x = −aε , x = aε , перпендикулярные большей полуоси,

называются директрисами эллипса.

Параметрическое уравнение эллипса имеет вид

	x = a cost,	0	≤ t ≤ 2π.	(1.47)
	y = bsin t,

Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых модуль разности расстояний от двух данных точек этой плоскости (фокусов гиперболы F1 и F2 ) есть

величина постоянная (меньше расстояния между фокусами и отлична от нуля).

Если оси координат по отношению к гиперболе расположить так, как указанонарис. 1.10, токаноническоеуравнениегиперболыимеетвид

26

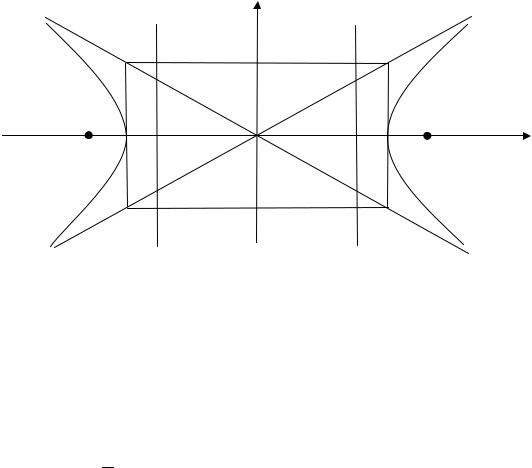
	x2	−	y2	=1.	(1.48)
	a2		b2

Точки А1(− а; 0 ) и А2 (а; 0 ) пересечения гиперболы с осью Ох на-

зываются вершинами гиперболы. Ось Ох называется действительной осью, а ось Оу – мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Расстояние между фокусами гиперболы обозначим через 2с, тогда полуфокусное рас-

стояние с связано с полуосями соотношением с2 − а2 = b2 .

−a

y

a

x =

x =

ε

ε

B2 (0; b)

A (−a; 0)

A2 (a; 0)

1

F2 (c; 0)

x

F1 (−c; 0)

0

B1 (0; −b)

Рис. 1.10

Две прямые

y = −b x ,

y = b x

(1.49)

a

a

называются асимптотами гиперболы. К ним приближаются ветви гиперболы при неограниченном удалении от начала координат.

Число ε = aс , где а – действительная полуось, называется эксцен-

триситетом гиперболы. Очевидно, что для гиперболы ε >1.

Две прямые x = −aε , x = aε , перпендикулярные действительной

полуоси, называются директрисами эллипса.

Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до некоторой данной

27

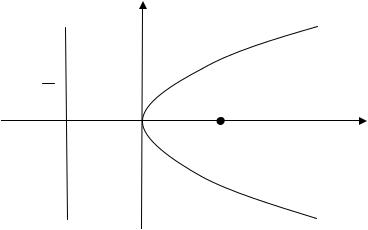
точки F этой плоскости, называемой фокусом, равно расстоянию до некоторой данной прямой, называемой директрисой (рис. 1.11).

y

x = − 2p

0	p			x
	F		; 0
		2

Рис. 1.11

Каноническое уравнение параболы в выбранной декартовой системе координат имеет вид

y2 = 2 px ,

(1.50)

где p – расстояние от фокуса до директрисы. В этой же системе координат уравнение директрисы имеет вид

x = −	p	.	(1.51)
2

Эксцентриситет параболы ε =1.

Замечание. Эллипс, гипербола и парабола и только эти кривые обладают общим геометрическим свойством – отношение расстояния от любой точки каждой из этих кривых до фокуса к расстоянию от этой точки до ближайшей директрисы есть величина постоянная, равная эксцентриситету ε.

1.4. Полярная система координат

Если на плоскости заданы фиксированная точка О, называемая полюсом, и исходящий из полюса луч с выбранной на нем единицей масштаба, называемый полярной осью, то говорят, что на плоскости задана полярная система координат. В этом случае положение любой точки М на плоскости определяется двумя числами r и ϕ, где r – расстояние

28

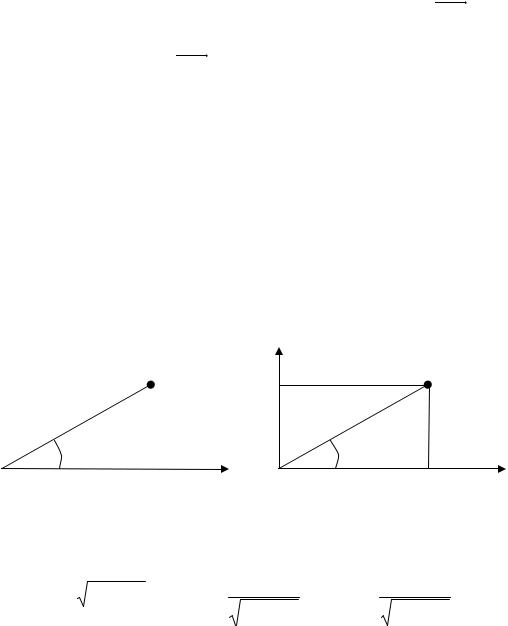
от точки М до точки О, ϕ – угол, образуемый вектором OM с положительным направлением полярной оси. Угол ϕ, отсчитываемый от

полярной оси до вектора OM в направлении против часовой стрелки, считается положительным, а отсчитываемый в противоположном направлении – отрицательным (рис. 1.12).

Обычно считают, что 0 ≤ ϕ< 2π, 0 ≤ r < ∞ . Если r = 0 , точка М совпадает с полюсом О и угол ϕ для нее не определен.

Пусть наряду с полярной системой координат на плоскости выбрана прямоугольная декартова система координат так, что начало координат совпадает с полюсом О, а ось Оx совпадает с полярной осью (рис. 1.13). Тогда прямоугольные координаты x и y точки М связаны с ее полярными координатами r и ϕ соотношениями

x = r cosϕ;

y = r sin ϕ.

(1.52)

y

M (r; ϕ)

x

M (x; y)

r

r

y

ϕ

ϕ

O

r

O

x

Рис. 1.12

Рис. 1.13

Из (1.51), в частности, вытекает, что

r =

x2 + y2 ; cos ϕ =

x

;

sin ϕ =

y

.

(1.53)

+ y2

x2

x2

+ y2

Рассмотрим далее применение вышеизложенных теоретических сведений к решению типовых задач.

Задача2. Даны координаты вершин пирамиды A1 A2 A3 A4 : A1 (3; 3; 9) ,

A2 (6; 9;1) , A3 (1; 7; 3) , A4 (8; 5; 8) . Найти: 1) длину ребра A1 A2 ; 2) угол между ребрами A1 A2 и A1 A4 ; 3) угол между ребром A1 A4 и гранью A1 A2 A3 ; 4) площадь грани A1 A2 A3 ; 5) объем пирамиды; 6) уравнение прямой A1 A2 ; 7) уравнение плоскости A1 A2 A3 ; 8) уравнение высоты, опущенной из вершины A4 на грань A1 A2 A3 .

29

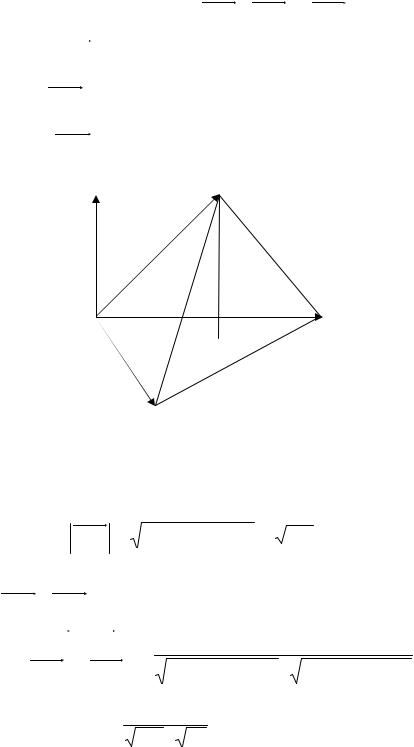
Решение. Сделаем схематический чертеж (рис. 1.14). По формуле (1.10) найдем координаты векторов A1 A2 , A1 A3 и A1 A4 :

A1 A2 ={6 − 3; 9 − 3;1 − 9}={3; 6;−8};

A1 A3 ={1 − 3;7 − 3; 3 − 9}={− 2; 4; − 6};

A1 A4 ={8 − 3;5 − 3; 8 − 9}={5; 2;−1}.

n

A4

A1

• D

A2

A3

Рис. 1.14

1) Длину ребра A1 A2 найдем по формуле (1.11):

A A =

32 + 62 + (−8)2 =

109 .

1

2

2) Угол ϕ между ребрами A1 A2 и A1 A4

найдем как угол между

векторами A1 A2 , A1 A4

по формуле (1.18):

cos ϕ =

A1 A2 A1 A4

=

3 5 + 6 2 + (−8) (−1)

=

A1 A2

A1 A4

32

+ 62 + (−8)2

52 + 22 + (−1)2

=

35

30 ≈ 0,6121,

109

откуда ϕ = arccos 0,6121 ≈52°15'.

3) Для нахождения угла α между ребром

A1 A4 и гранью

A1 A2 A3

найдем нормальный вектор n , перпендикулярный плоскости

A1 A2 A3 ,

30