
Волк_Высшая математика.2010
.pdf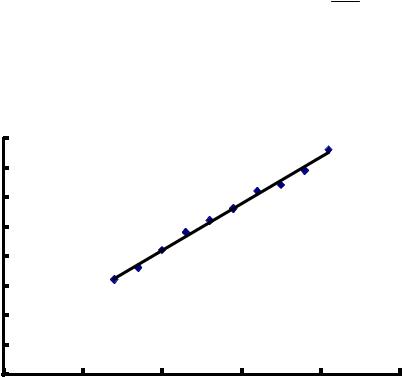

Для нахождения коэффициентов а и b запишем нормальную систему (13.12). Для вычисления коэффициентов системы (13.12) составим табл. 13.7.
|
|
|
|
Таблица 13.7 |
|
x |
y |
x2 |
x y |
|
i |
i |
i |
i i |
1 |
14 |
32 |
196 |
448 |
2 |
17 |
36 |
289 |
612 |
3 |
20 |
42 |
400 |
840 |
4 |
23 |
48 |
529 |
1104 |
5 |
26 |
52 |
676 |
1352 |
6 |
29 |
56 |
841 |
1624 |
7 |
32 |
62 |
1024 |
1984 |
8 |
35 |
64 |
1225 |
2240 |
9 |
38 |
69 |
1444 |
2622 |
10 |
41 |
76 |
1681 |
3116 |
∑ |
275 |
537 |
8305 |
15942 |
Система (13.12) для нашего примера имеет вид:10b + 275a = 537,
275b + 8305a = 15942.
Из нее находим коэффициенты a и b : a = 1,58 ; b = 10,2 . Искомая эмпирическая функция: y = 1,58x +10,2 . На рис. 13.3 построим график
полученной прямой. График эмпирической зависимости соответствует точечной диаграмме.
162
13.A1 (4; 2; 0); A2 (6;1;1); A3 (4; 6; 6); A4 (1; 2; 6).
14.A1 (3; 5;10); A2 (5; 5; 4); A3 (3; 8; 4); A4 (5; 8; 2).
15.A1 (4; 6; 3); A2 (0; 7;1); A3 (4;1; 5); A4 (3; 9; 8).
16.A1 (5; 7; 8); A2 (9; 5; 5); A3 (−3; 7;1); A4 (6; 9; 2).
17. A1(4; 9; 3); A2 (2; 4; 3); A3 (7; 6; 3); A4 (3; 6; 7).
18.A1 (1; 9; 9); A2 (3; 5; 4); A3 (5; 8; 3); A4 (6; 4; 8).
19.A1 (1; 7; 3); A2 (3; 3; 9); A3 (6; 9;1); A4 (8; 5; 8).
20.A1 (−1;1; 6); A2 (3;1; 4); A3 (−1; 6;1); A4 (0; 4; −1).
Задача 21. Составить каноническое уравнение эллипса, большая полуось которого равна 10, эксцентриситет 0,6 и фокусы лежат на оси Ox . Изобразить эллипс на рисунке.
Задача 22. Составить каноническое уравнение эллипса, сумма полуосей которого равна 8 и расстояние между лежащими на оси Ox фокусами 8. Изобразить эллипс на рисунке.
Задача 23. Составить каноническое уравнение эллипса, если расстояния от лежащего на оси Oy фокуса до концов его большой оси
равны 9 и 1. Изобразить эллипс на рисунке.
Задача 24. Составить каноническое уравнение эллипса, вытянутого вдоль оси Oy , если расстояние между директрисами равно 12 и рас-
стояние между фокусами равно 8. Изобразить эллипс на рисунке.
Задача 25. Составить каноническое уравнение гиперболы, фокусы которой лежат на оси Oy , действительная полуось равна 6, а эксцен-
триситет 53 . Изобразить гиперболу на рисунке.
Задача 26. Составить каноническое уравнение гиперболы, если расстояние между лежащими на оси Ox фокусами равно 20, а уравне-
ние асимптот y = ± 43 x . Изобразить гиперболу на рисунке.
164

Задача 27. Составить каноническое уравнение гиперболы, если расстояние между лежащими на оси Oy фокусами равно 20, а рас-
стояние между вершинами 12. Изобразить гиперболу на рисунке.
Задача 28. Составить каноническое уравнение гиперболы, если расстояние между лежащими на оси Oy фокусами равно 26, сумма
полуосей равна 17, а действительная полуось больше мнимой. Изобразить гиперболу на рисунке.
Задача 29. Составить каноническое уравнение параболы, вершина которой совпадает с началом координат, а прямая x = 3 является директрисой. Изобразить параболу на рисунке.
Задача 30. Составить каноническое уравнение параболы, вершина которой совпадает с началом координат, а фокус находится в точке F(0; −1,5) . Изобразить параболу на рисунке.
Тема 2. Предел и непрерывность функции
Задачи 31–40. Найти предел функции, не используя при этом правило Лопиталя.
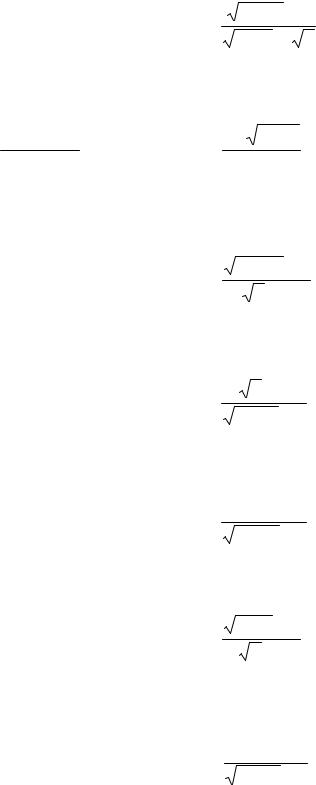
31. a) lim |
3x2 + x −10 |
; |
б) lim |
1 + x − 1 + 2x |
; |
||
x→∞ |
x2 + 2x −3 |
|
x→0 |
x2 +3x |
|
||
в) lim |
1−cos 2x |
; |
|
|
2x +3 |
x−1 |
|
x sin 3x |
|
г) lim |
2x +5 |
. |
|
||
x→0 |
|
|
x→∞ |
|
|
||
32. a) lim |
x2 −7x +12 |
; |
|
б) lim |
|
5 + x −3 |
; |
||||||||
|
|
|
|
x − 4 |
|||||||||||
x→3 |
x2 −8x +15 |
|
|
x→4 |
|
|
|||||||||
в) lim |
|
|
xtgx |
; |
|
|
|
г) lim(1 − 5x) |
x+1 |
|
|||||
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
x |
|||||||||||
|
|
|
|
|
|||||||||||
x→0 1 − cos 4x |
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|||
33. a) lim |
x3 + x2 +3x |
|
; |
|
б) lim |
|
x |
; |
|||||||
|
|
|
4 + x − 2 |
||||||||||||
x→∞ |
2x3 − x +10 |
|
|
x→0 |
|
|
|||||||||
в) lim |
tg2x −sin 2x |
|
г) lim |
x |
1−3 x |
|
|||||||||
x2 |
|
|
|
; |
|
|
|
. |
|
||||||
|
|
|
|
|
|||||||||||
x→0 |
|
|
|
|
x→∞ |
x −1 |
|
|
|||||||
165
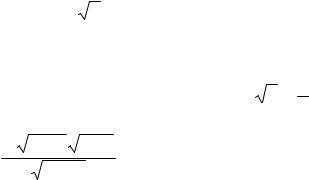
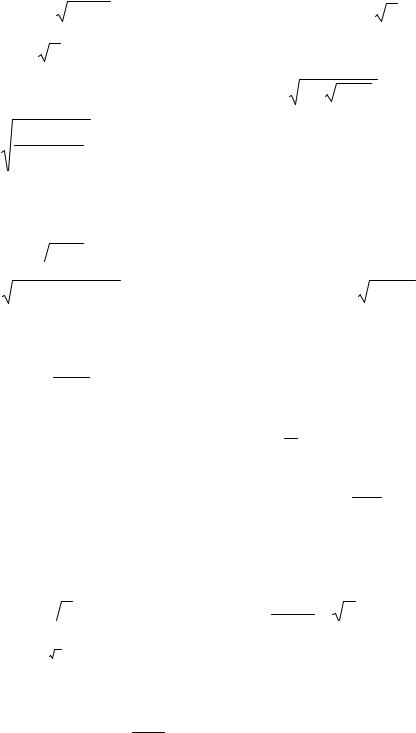


 x
x 