
Волк_Высшая математика.2010
.pdf
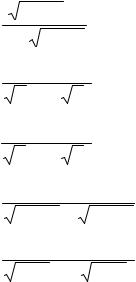

131.y = x2 , x = y2 .
132.y = 2x − x2 , y = 0 .
133.xy = 4, x =1, x = 4, y = 0 .
134.y =1 + cos x, x = −π2 , x = π2 , y = 0 .
135.y =1 + sin x, x = 0, x = π, y = 0 .
136.y = 1 + ex , x = 0, x = 1, y = 0.
137.+ y2 =1. 4 9
138.y = x2 +1, y = 3, x = 0 .
139.x = 4 y − y2 , x = 0 .
140.y = x3 , y =1, x = 0 .x2
Задачи 141–150. Вычислить несобственный интеграл (или доказать его расходимость).
141. |
+∞ |
|
|
|
|
|
|
|
|
|
142. |
1 |
|
dx . |
|||||
∫ xe−x2 dx . |
|
∫ |
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
1 − x |
|
|
|
||
|
+∞ |
ln xdx |
|
|
|
|
e |
|
dx |
|
|
|
|
|
|||||
143. |
∫ |
. |
|
|
144. |
∫ |
|
. |
|
|
|
||||||||
|
|
|
xln x |
|
|
|
|||||||||||||
|
2 |
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
+∞ |
|
|
dx |
|
|
|
|
+∞ dx |
|
|
|
|
||||||
145. |
∫ |
|
|
|
|
|
|
. |
|
146. |
∫ |
|
|
|
. |
|
|
||
9x |
2 |
+1 |
|
|
xln x |
|
|
||||||||||||
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
+∞ |
|
x2 dx |
|
|
|
|
2 |
|
dx |
|
|
|
|
|||||
147. |
∫ |
|
|
|
|
|
|
|
. |
|
148. |
∫ |
|
|
|
|
|
. |
|
|
x |
3 |
+ |
|
|
(x −1) |
2 |
||||||||||||
|
0 |
|
|
1 |
|
|
1 |
|
|
|
|||||||||
|
+∞ |
|
|
|
|
|
dx |
|
|
|
2 |
|
dx |
|
|
|
|
||
149. |
∫ |
|
|
|
|
|
|
. |
150. |
∫ |
|
|
|
2 . |
|||||
|
2 |
|
+ 2x + 2 |
|
4 − x |
||||||||||||||
|
−1 x |
|
|
|
|
0 |
|
|
|
||||||||||
Тема 7. Обыкновенные дифференциальные уравнения
Задачи 151–160. Найти общее решение дифференциальных уравнений первого порядка.
173

151. |
xy′ + y = 3. |
|
|
|
|
|
152. |
xy′ − y = |
x2 |
− y2 . |
||||||||||||
|
(1 + x |
2 |
)y |
′ |
|
2xy = (1 + x |
2 |
) |
2 |
|
|
|
′ |
|
|
|
|
|
y |
|
||
153. |
|
− |
|
|
. |
154. |
xy |
− y = y ln x . |
||||||||||||||
|
|
|
|
|
||||||||||||||||||
155. |
y′ − y = ex . |
|
|
|
|
|
156. |
2x3 y′ = y(2x2 |
− y2 ). |
|||||||||||||
157. |
y′ + 2xy = 3x2 e−x2 . |
|
|
|
|
158. |
2x2 y′ + x2 |
+ y2 = 0 . |
||||||||||||||
|
(x +1)y |
′ |
|
|
|
3 |
|
|
|
|
|
|
′ |
|
|
y |
|
|
||||
|
+ y |
= x + x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
159. |
|
|
|
|
160. |
xy |
= y ln x . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
Задачи 161–170. Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка.
|
|
′′ |
|
|
|
y′ |
|
|
2 |
|
|
′′ |
|
|
|
|
|
161. |
y |
+ 2 x = x . |
162. |
y |
= ln x . |
|
|
||||||||||
|
|
|
|
|
|||||||||||||
163. |
y |
′′ |
+ y |
′ |
tg x = sin 2x . |
164. |
y |
′′ |
|
′ |
2 |
||||||
|
|
|
|
(1 + y) − 5(y ) |
= 0 . |
||||||||||||
165. |
|
′′ |
|
|
|
|
′ |
. |
|
166. |
yy |
′′ |
′ 2 |
|
|
||
y xln x = y |
|
|
|
= (y ) . |
|
|
|||||||||||
167. |
y′′ − y′ctg x = sin x . |
168. |
(y − 2)y′′ = 2(y′)2 . |
||||||||||||||
169. |
xy′′ = y′. |
|
|
170. |
y′′tg x = y′+1. |
|
|
||||||||||
Задачи 171–180. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
171. |
y |
′′ |
+ 4 y = 0, |
y(0) = 0, |
′ |
|||||||
|
y (0) = 2 . |
|||||||||||
172. |
y |
′′ |
− 6 y |
′ |
+ 9 y = 0 , |
y(0) =1, |
′ |
|||||
|
|
y (0) =3 . |
||||||||||
173. |
y |
′′ |
+ 4 y |
′ |
+ 4 y = 0 , |
y(0) =1, |
′ |
|||||
|
|
y (0) = −1. |
||||||||||
174. |
y |
′′ |
+ 25y = 0 , |
y(0) =1, |
′ |
|||||||
|
y (0) =10. |
|||||||||||
175. |
y |
′′ |
+ y |
′ |
− 20 y = 0 , |
y(0) = 2, |
′ |
|||||
|
|
y (0) =1. |
||||||||||
176. |
4 y |
′′ |
+ 4 y |
′ |
+ y = 0 , |
y(0) = 0, |
′ |
|||||
|
|
y (0) = 2 . |
||||||||||
177. |
y |
′′ |
+ 6 y |
′ |
+13y = 0 , |
y(0) =1, |
′ |
|||||
|
|
y (0) = −3. |
||||||||||
178. |
y |
′′ |
+8y |
′ |
+16 y = 0 , |
y(0) = 2, |
′ |
|||||
|
|
|
y (0) = −1. |
|||||||||
179. |
y |
′′ |
+ 2 y |
′ |
+ 2 y = 0 , |
y(0) = 3, |
′ |
|||||
|
|
y (0) = 2 . |
||||||||||
180. |
y |
′′ |
+5y |
′ |
= 0 , |
y(0) = 7, |
′ |
|||||
|
|
|
y (0) = −20 . |
|||||||||
174
Задачи 181–190. Найти общее решение линейного дифференциального уравнения второго порядка.
181.y′′−3y′+ 2 y = 4 e3 x .
182.y′′− 4 y = 8x3 .
183.y′′ + 4 y′ +13y = (18x + 6)ex .
184.y′′ + 6 y′ + 8y = 7e3 x .
185.y′′ − 2 y′ + y = 4sin 2x − 3cos 2x .
186.y′′+ 2 y′+10 y =18 e−x .
187.y′′ − 6 y′ + 9 y = 2cos x +14sin x .
188.y′′ − 6 y′ + 5y = 5x2 −12x + 7 .
189.y′′ + 3y′ = (4x − 2)e−x .
190.y′′− 2 y′+ 26y = 25 cos x + 2 sin x .
Задачи 191–200. Найти решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
|
dx |
= −3x − y, |
|
|
|
191. |
dt |
x(0) = 0, |
y(0) =1. |
||
|
|
dy |
= x − y, |
|
|
|
|
|
|
||
|
dt |
|
|
|
|
|
dx |
= −7x + y, |
|
|
|
192. |
dt |
x(0) = 0, |
y(0) =1. |
||
|
|
dy |
= −2x −5y, |
|
|
|
|
|
|
||
|
dt |
|
|
|
|
|
dx |
= 2x + y, |
|
|
|
193. |
dt |
x(0) = 2, |
y(0) = −1. |
||
|
|
dy |
= 6x + y, |
|
|
|
|
|
|
||
|
dt |
|
|
|
|
|
dx |
= 3x − y, |
|
|
|
194. |
dt |
x(0) = 2, |
y(0) = 3. |
||
|
|
dy |
= 4x − y, |
|
|
|
|
|
|
||
|
dt |
|
|
|
|
175
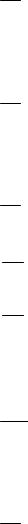

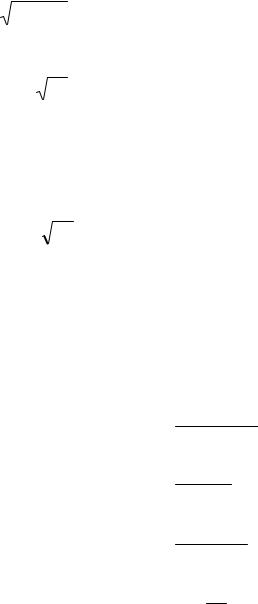
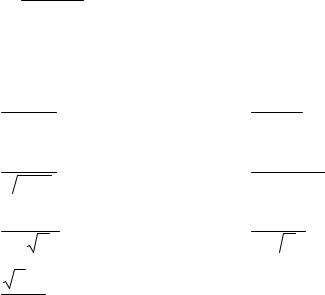



 n
n


 1
1