Волк_Высшая математика.2010

Решение. По условию Mξ = 400 . Для						показательного закона рас-
пределения M		=	1	= 400 . Следовательно,		λ =	1	. Искомую вероят-
	ξ		λ			400
ность p(ξ ≥ 600)			будем искать, используя вероятность противопо-
ложного события и формулу (12.47):
p(ξ ≥ 600) =1 − p(0 ≤ ξ < 600) =1−(e−					0	− e−600400 )= e−			3	≈ 0,22 .
					400				2

Задача 14. Случайная величина ξ распределена по нормальному закону. Математическое ожидание и среднеквадратическое отклонение этой величины соответственно равны 30 и 10.

Найти: а) вероятность попадания случайной величины в интервал (20; 50); б) вероятность p( ξ − Мξ < σξ ) .

Решение. а) По условию α = 20 ; β = 50; a = 30 ; σ =10 . По формуле (12.49) и прил. 2 получим:

p(20 < ξ < 50) = Φ 50 −30 −Φ 20 −30 = Φ(2) −Φ(−1) =10 10

= Φ

(

2

)

( )

= 0,4772 +0,3413 = 0,8185 .

+ Φ

1

б) По формуле (12.50)

получим:

p(

ξ − Мξ

σ

ξ

= 2 0,3413 = 0,6826 .

< σξ) =

2Φ

= 2Φ(1)

σξ

151

Тема 13. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

13.1. Статистический ряд и его описание

Математическая статистика занимается установлением закономерностей, которым подчинены массовые, однородные, случайные явления, на основеизучениястатистических данных– результатовнаблюдений.

Генеральной совокупностью называется множество всех возможных значений случайной величины ξ.

Выборкой объема n называется множество x1, x2 , , xn наблюдае-

мых значений изучаемой случайной величины, которые соответствуют n независимым испытаниям (опытам).

Размах выборки W – разность между максимальным и минимальным значениями элементов выборки: W = xmax − xmin .

Статистический ряд – совокупность пар (xi ; ni ), i =1,k , где xi − разные элементы выборки, ni – частота появления выборочного

k

значения xi . Очевидно, что ∑ni = n .

i=1

Величины ωi = nni , i =1,k называются относительными частотами,

k

и для них ∑ωi =1.

i=1

Обычно статистический ряд записывают в виде табл. 13 1.

					...	Таблица 13.1
xi		x1		x2			xk
ni	n1			n2	...	nk
ωi		n1		n2	...		nk
		n		n			n

При изучении непрерывной случайной величины или при большом объеме выборки ее элементы объединяются в группы, и записывают интервальный статистический ряд (табл. 13.2).

Если все интервалы имеют одинаковую длину h, то h = Wk . Коли-

чество интервалов выбирают по формуле

k =1+3,2lg n .

(13.1)

152

						Таблица 13.2
Интервал	[xmin ; x2 )			[x2 ; x3 )	...	[xk ; xmax ]
Середина интервала		x1*		x*2	...		x*k
Частота	n1			n2	...	nk
Относительная частота		n1		n2	...		nk
		n		n			n

Полигоном частот статистического ряда называется ломаная линия с вершинами в точках (xi ; ni ), i =1, k .

Полигоном относительных частот статистического ряда называ-

	ni
ется ломаная линия с вершинами в точках xi ;	, i =1, k .
	n

Гистограммой относительных частот статистического интер-

вального ряда называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группирования с высотой

	прямоугольников	ni	. Площадь каждого прямоугольника равна ni ,
		nh
						n
	а сумма площадей всех прямоугольников равна 1.
	Эмпирической функцией распределения F* (x) называется функция
			F* (x) = ∑	ni	.	(13.2)
			xi < x n

Эта функция непрерывна слева, обладает всеми свойствами функции распределения случайной величиныF(x) = P(ξ < x) и является

приближенным представлением последней.

13.2. Статистическая оценка параметров распределения

Анализ полигона, гистограммы и эмпирической функции распределения дает возможность сделать предположение о законе распределения изучаемой случайной величины. Данный закон может быть установлен и на основании теоретических предположений.

Затем возникает задача оценки параметров предполагаемого закона распределения по полученной выборке. Оценкой параметра называют функцию от выборки, значение которой является приближенным

153

значением параметра. Оценки параметров подразделяются на точечные и интервальные.

Точечные оценки задаются одним числом, а интервальные – границами доверительного интервала. Точечные оценки должны удовле-

творять определенным требованиям.

~

Несмещенной называется статистическая оценка Θ, математиче-

ское ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. M (Θ~ )= Θ.

Эффективной называется статистическая оценка, которая (при данном объеме выборки) имеет минимально возможную дисперсию.

Состоятельной называется статистическая оценка, которая при n → ∞ стремится по вероятности к оцениваемому параметру, т. е.

P(

~

< ε)→ 1.

Θ − Θ

n→∞

Точечной оценкой математического ожидания является выбороч-

ное среднее

1

k

x =

∑ xi ni .

(13.3)

n i=1

Для интервального статистического ряда (табл. 13.2)

k

x =

1 ∑ xi ni .

(13.4)

n i=1

Точечной оценкой дисперсии является выборочная дисперсия

в ,

D

которая вычисляется по формуле

1

k

2

1 k

2

2

Dв =

.

∑ ni (xi − x) =

∑ xi ni − x

n i=1

n i=1

Эта оценка является смещенной. Несмещенной оценкой дис-

персии Dξ является s2 = n n−1 Dв . Для статистического ряда выборки объема n она вычисляется по формуле

		1	n	1	n	n
	s2 =		∑(xi − x)2 =		∑ xi2 −			x2.
						n −1
		n −1 i=1		n −1 i=1

Для интервального статистического ряда (табл. 13.2)

s2 =	1 ∑(xi* − x)2 ni =		1 ∑(xi* )2 ni − n				x 2 .
		k		k
	n −1	i=1	n −1	i=1	n −1

(13.5)

(13.6)

154

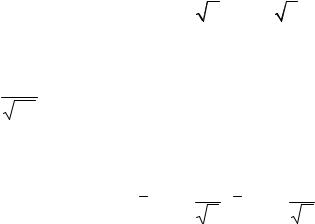
Оценкой среднеквадратического отклонения служит корень из несмещенной оценки дисперсии, т. е. s.

Доверительным интервалом для параметра Θ называется интервал (α1; α2 ), который покрывает неизвестный параметр Θ с заданной

надежностью γ =1−α, т. е. P(α1 < Θ < α2 ) = γ. Число γ =1 − α называется доверительной вероятностью, а значение α – уровнем значимости. На практике обычно используют уровни значимости: 0,1; 0,05; 0,01.

Доверительный интервал для математического ожидания нормально распределенной случайной величины ξ при данном уровне

значимости α и известной дисперсии Dξ = σξ2 имеет вид

						σξ		σξ
				x −tγ			, x +tγ		,		(13.7)
						n
								n
где tγ определяется из условия 2Φ(tγ )= γ =1 − α, или											Φ(tγ )= γ / 2 , и
	1	x	t2
Φ(x) =		∫e−		dt − функция Лапласа (см. прил. 2).
			2
	2π 0
При неизвестной дисперсии генеральной совокупности использу-
ется формула
					−tα; ν	s	, x +tα; ν		s		(13.8)
				x		n			n	,
где tα; ν	определяется с помощью таблицы значений распределения

Стьюдента по данному числу степеней свободы ν = n −1 и уровню

значимости α (прил. 3). Здесь s − оценка среднеквадратического

отклонения (13.4). Отметим, что при объеме выборки n > 30 вместо

распределения Стьюдента можно пользоваться нормальным распределением.

Задача 1. Даны результаты наблюдения случайной величины, записанные в табл. 13.3.

1.Построить гистограмму относительных частот.

2.Найти эмпирическую функцию распределения и построить ее

график.

3.Определить гипотетическую плотность закона распределения.

4.Вычислить выборочное среднее значение x и несмещенную

оценку дисперсии s2 .

155

Таблица 13.3

36	39	43	45	26	34	50	33	36	57
29	40	31	34	17	47	39	35	41	28
25	30	39	36	49	42	24	27	20	52
36	33	18	32	56	37	40	29	31	46
38	19	28	33	42	26	35	37	34	48
44	22	36	49	30	27	40	32	41	43
45	38	24	37	46	36	29	25	39	52
50	21	38	34	41	47	29	31	28	35
44	55	39	30	27	32	34	40	54	36
25	53	45	33	43	37	26	42	28	51

5)Найти доверительный интервал для математического ожидания

сдоверительной вероятностью γ = 0,95.

Решение. Поскольку объем выборки достаточно большой: n =100 , то строим интервальный статистический ряд. Количество интервалов вычисляем по следующей формуле (13.1):

k =1 + 3,2lg100 =1 + 6,4 = 7,4 .

Принимаем k = 7 . Размах выборки W = 57 −17 = 40.

Длина интервала: h = 407 . Принимаем h = 6 .

Находим количество элементов выборки в каждом интервале и

строим интервальный статистический ряд (табл. 13.4).

1) Строим гистограмму относительных частот (рис. 13.1) (значе-

ние высот вычислено и записано в четвертой строке табл. 13.4).

Таблица 13.4

Интервал					[17–23)	[23–29)	[29 –35)	[35–41)	[41–47)	[47–53)	[53–59]
[xi – xi + 1)
Середина интер-					20	26	32	38	44	50	56
вала, xi
Частота, ni					6	15	22	26	16	10	5
Относительная
частота, ωi		=	ni		0,06	0,15	0,22	0,26	0,16	0,1	0,05
			n
Высота,	ni				0,01	0,025	0,037	0,043	0,027	0,017	0,008
	hn
156

ni

hn

0,04

0,03

0,02

0,01

O	17	23	29	35	41	47	53	59	x

Рис. 13.1

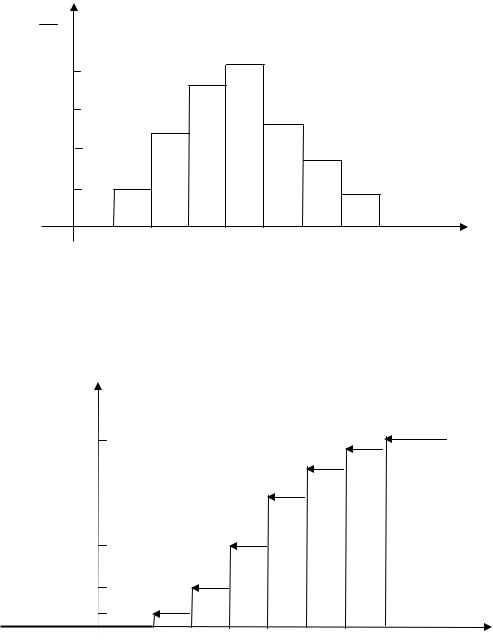
Строим график функции распределения (рис. 13.2).

F (x)

1,00

0,43

0,21

0,06

O

x

20 26 32 38 45 50 56

Рис. 13.2

2) Найдем эмпирическую функцию распределения F (x) по фор-

муле (13.2). Данная функция является кусочно-постоянной, ее значе-

ния получаются накоплением относительных частот в точках xi и изменяются в пределах от 0 до 1.

Запишем функцию в следующем виде:

157

0,	если	x ≤ 20,
	если	20 < x ≤ 26,
0,06,
0,21,	если	26 < x ≤ 32,
	если	32 < x ≤ 38,
0,43,
F (x) =		38 < x ≤ 44,
0,69,	если
0,85,	если	44 < x ≤ 50,
	если	50 < x ≤ 56,
0,95,
	если	x > 56.
1,

3)По виду гистограммы выдвигаем гипотезу о нормальном законе распределения случайной величины. Данный закон содержит два параметра a и σ: Mξ = a ; Dξ = σ2 .

4)Найдем точечную оценку математического ожидания по фор-

муле (13.4):

x = 1001 (20 6 + 26 15 + 32 22 + 38 26 + 44 16 +50 10 +56 5) = = 3686100 = 36,86 .

Несмещенную оценку дисперсии найдем по формуле (13.6):

s2 = 991 (16,862 6 +10,862 15 + 4,862 22 +1,142 26 + 7,142 16 +

+13,142 10 +19,142 5) = 8402,0499 =84,87 .

Тогда s = 9,2 .

Функция плотности соответствующего нормального закона распределения имеет вид

	1	e	−	(x−36,86)2
f (x) =				2 9,22	.
	9,2 2π

5) Найдем доверительный интервал для математического ожидания при неизвестной дисперсии по формуле (13.8) с уровнем значимости a = 0,05 . Число степеней свободы будет ν = n −1 = 99 . По прил. 3 определим tα; ν = t0,05; 99 =1,98 .

158

Тогда получим:
	−1,98	9,2	; 36,86	+1,98	9,2		= (35,04; 38,68).
36,86		100			100

13.3. Эмпирические зависимости. Метод наименьших квадратов

При исследовании многочисленных физических, химических, технологических и других процессов очень часто сталкиваются со следующей задачей: в итоге опыта получен ряд значений переменных x и y , требуется по полученным данным найти аналитическое

выражение зависимости между x и y . Такая зависимость называет-

ся эмпирической.

Пусть заданы результаты наблюдений (табл. 13.5).

						Таблица 13.5
X	x1		x2		…		xn
Y	y1		y2		…		yn
Нужно получить такую эмпирическую зависимость
	y = f (x; a0 ; a1; a2 ; ...; am ),						(13.9)
где a0 , a1, a2 , …, am –		такие параметры,			при которые		значения
y = f (x; a0 ; a1; a2 ; ...; am )		в точках xi мало			отличались от опытных

данных yi , i =1, n.

Задача определения эмпирической зависимости состоит из двух этапов:

1) определение вида функциональной зависимости (выбор класса функций, которому должна принадлежать искомая функция

y= f (x; a0 ; a1; a2 ; ...; am );

2)определение параметров эмпирической зависимости.

Определение вида зависимости может быть произведено на основе теоретических представлений о характере изучаемой зависимости или из геометрических соображений. На плоскости xOy строят точки

M i (xi ; yi ) , i =1, n и по характеру их расположения выбирают вид функциональной зависимости.

159

Например, расположение экспериментальных точек может навести на мысль о линейной или квадратичной, или экспоненциальной, или другой зависимости.

Однако общего метода для нахождения наилучшего типа эмпирической зависимости, соответствующей опытным данным, указать нельзя.

После того, как определен класс, которому должна принадлежать искомая эмпирическая зависимость, встает вопрос о нахождении конкретных значений параметров a0 , a1, a2 , …, am .

Одним из основных методов нахождения параметров эмпирической зависимости является метод наименьших квадратов. Этот метод не решает вопроса о выборе общего вида аналитической функции, а дает возможность при заданном типе аналитической функции подобрать наиболее вероятные значения для ее параметров.

Сущность метода наименьших квадратов состоит в том, что параметры a0 , a1, a2 , …, am выбираются из условия минимума суммы

квадратов уклонений

S = n	f	(	x; a ; a ; a ; ...; a			m )	− y		2 .	(13.10)
∑			0	1	2			i
i=1
Известно, что если	в	качестве			функции			f	берется	многочлен
f (x) = a0 + a1x + a2 x2 +	+ am xm ,			то	функция				S = S (a0 ; a1; a2 ; ...; am )

имеет одну точку экстремума, в которой достигается минимум. В этом случае коэффициенты многочлена a0 , a1, a2 , …, am представляют со-

бой решение системы линейных уравнений m +1-го порядка:

		n	n	2		n	m	n
a0n		+ a1 ∑ xi	+ a2 ∑ xi		+…	+ am ∑ xi		= ∑ yi ,
	n	i=1	i=1			i=1		i=1
		n	n			n		n
a0	∑ xi	+ a1 ∑ xi2	+ a2 ∑ xi3 +…			+ am ∑ xim+1		= ∑ xi yi ,	(13.11)
	i=1	i=1	i=1			i=1		i=1
	n	n	n			n		n
a0	∑ xim + a1 ∑ xim+1		+ a2 ∑ xim+2 +…+ am ∑ xi2m					= ∑ xim yi .
	i=1	i=1	i=1			i=1		i=1

Данная система называется нормальной и решается любым известным методом (Гаусса, Крамера, матричным).

В частном случае, когда y зависит от x линейно: y = ax +b , система для нахождения коэффициентов имеет вид:

160