Волк_Высшая математика.2010

в качестве которого можно взять векторное произведение векторов A1 A2 и A1 A3 , вычисляемое по формуле (1.16):

n = A A × A A =

i

j

k

6

−8

i −

3

−8

j +

3 6

k =

3

6

−8

=

1

2

1

3

4

− 6

− 2

− 6

− 2 4

− 2

4

− 6

= −4 i + 34 j + 24 k .

Синус искомого угла α равен косинусу угла β между векторами n

и A1 A4 , так как сумма этих углов равна π2 . Поэтому

										n A1 A4																						−4 5 +34 2 + 24															(		−1
	sin α = cosβ =																										=																						)						=
										n								A1 A4										(			)	2 +342 + 242														52 +			22 +			(	)	2
																														−4																							−1
				=		24															≈ 0,1048, т. е. α ≈ arcsin 0,1048 ≈6°1'.
					1748										30
	4) Площадь грани A1 A2 A3 вычислим по формуле (1.20):
S =	1		A A × A A							= 1										n			= 1					(− 4)2				+ 342 + 242											=			1748 =							437 ≈ 20,9 .
	2		1	2	1	3									2								2																							2
	5) Объем V пирамиды A1 A2 A3 A4																															найдем по формулам (1.17) и (1.21):
					V =				1							A A A A A A																			1							3	6			−8
																																		=								− 2 4				− 6			=
							6								1						2						1	3		1		4		6
																																										5	2			−1
					= 1			3								4 − 6											−	6		− 2 − 6							+ (−8)								− 2			4			=
					6											2							−1							5				−1												5		2

=16 3 8 − 6 32 −8 (−24) = 16 24 = 4 (куб. ед.).

6)Уравнение прямой A1 A2 найдем по формуле (1.33):

x −3

=

y −3

=

z −9

, т. е.

x −3

=

y −3

=

z −9

.

6 −3

3

9 −3 1 −9

6

−8

31

7) Уравнение плоскости A1 A2 A3 найдем по формуле (1.38):

x −3

y −3 z −9

x −3 y −3 z −9

6 −3

9 −3

1 −9

= 0 , т. е.

3

6

−8

= 0 ;

1 −3 7 −3

3 −9

− 2

4

− 6

(x −3)

6

−8

− (y −3)

3 −8

+ (z −9)

3 6

= 0;

4

− 6

− 2

− 6

− 2 4

− 4(x −3) + 34( y −3) + 24(z −9) = 0.

Отсюда, − 4x + 34 y + 24z −306 = 0 , или 2x −17 y −12z −153 = 0 –

искомое уравнение плоскости.

8) Из полученного выше уравнения плоскости следует, что ее нормальный вектор n ={2; −17; −12}.

Нормальный вектор n перпендикулярен плоскости A1 A2 A3 , поэтому

его можно взять за направляющий вектор высоты, опущенной из вершины A4 на эту плоскость. Следовательно, уравнение этой высоты

можно найти по формуле (1.33):

x 2−8 = y−−175 = z−−128 .

Задача 3. Найти уравнение окружности, описанной около тре-

угольника с вершинами А(–1; 1), В(2; –1), С(4; 0).

Решение. Сначала найдем координаты центра окружности. Центр окружности, описанной около треугольника, лежит на пересечении перпендикуляров, проведенных к серединам сторон треугольника.

Поэтому для решения этой задачи поступим следующим образом:

1)составим уравнения сторон AB и AC;

2)найдем координаты середин сторон AB и AC;

3)составим уравнения прямых, перпендикулярных сторонам AB

иAC и проведенных через их середины;

4)найдем координаты центра окружности;

5)найдем радиус описанной окружности;

6)запишем уравнение описанной окружности.

Для наглядности решения сделаем рис. 1.15.

1) Уравнения сторон AB и AC найдем по формуле (1.28). Уравнение стороны AB будет:

32

x −

(

−1

y −1

x +1

y −1

2

1

2

)

=

,

или

=

, т. е.

y = − 3 x +

3 ;

kAB = −

3 .

2 −

(

−1

−1 −1

3

−2

)

Уравнение стороны AС:

x − (−1)

=

y −1

,

или

x +1

=

y −1

,

т. е.

y = −

1 x +

4

;

kAC = −

1 .

4 − (−1)

5

−1

5

0 −1

5

5

2) Найдем координаты точек M и N, являющихся серединами сторон AB и AC соответственно, по формулам

xM

=

xA + xB

=

−1 + 2

=

1

; yM

=

yA + yB

=

1−1

= 0 ;

2

2

2

2

2

xN

=

xA + xC

= −1 + 4

=

3

; yN

=

yA + yC

=

1 + 0

=

1 .

2

2

2

2

2

2

Итак, M 1

; 0

и N

3

; 1

– середины сторон AB и AC.

2

2

2

3) Для составления уравнений прямых, проходящих через точки M и N перпендикулярно сторонам треугольника, используем формулу (1.30), найдяпредварительноугловыекоэффициентыпрямыхизусловия(1.31).

Так как

kAB = −

2

(см.

найденное

уравнение прямой

AB),

то

1

= 3 ,

3

k

= −

значит,

уравнение первой прямой, проходящей через

1

kAB

2

точку М, имеет вид

(y − y

M

) = k (x − x

M

),

т. е. y − 0 = 3

x −

1 , или

y = 3 x − 3 .

1

2

2

4

2

Поскольку kAC = −

1

(см. найденное уравнение прямой AC),

то

1

5

k2

= −

= 5 , значит, уравнение второй прямой, проходящей через

kAC

= 5 x −

3 , или

точку N,

имеет вид

y − y

N

= k

2

(x − x

N

), т.

е. y − 1

2

2

y= 5x − 7 .

4)Решив систему из двух уравнений, найдем координаты точки О1 – точкипересеченияпрямых, являющейсяцентромискомойокружности:

33

y =	3 x −	3	,			3 x − 3 = 5x −7,		x =	25	,
									14
	2	4				2	4			25		27 .
y = 5x −7						y = 5x −7		y = 5			−7 =
										14		14
Итак, точка O1			25		;	27	– центр искомой окружности.
			14			14

y

	2	O1
A	1	N
	O		C
−1	M 1	2	4	x

–1

B

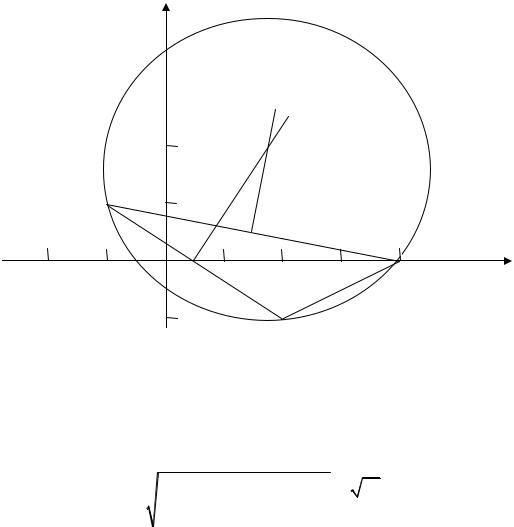
Рис. 1.15

5) Радиус R описанной окружности равен расстоянию от центра окружности до любой из вершин треугольника. Расстояние между точками О1 и А в соответствии с формулами (1.10) и (1.11) равно

O1 A =	25		2		27		2		10	= R .
		− 2		+		− 2		=
									14
	14			14

6) По формуле (1.43) запишем уравнение искомой окружности:

		25	2		27		10
	x −			+ y −		=			.
		14					196
					14

Задача 4. Оси эллипса совпадают с осями координат. Большая полуось расположена на оси Ох. Записать уравнение эллипса и сделать

34

чертеж с изображением директрис, если известно, что расстояние между фокусами равно 2c = 6 , а эксцентриситет ε = 53 .

Решение. Из условия задачи вытекает, что c = 3 . Из определения эксцентриситета имеем ε = ac = a3 = 53 , следовательно a = 5 . По формуле,

связывающей а, b и c, находим

b = a2 −c2 = 25 −16 = 4 .

Следовательно, искомое уравнение имеет вид

x2 + y2 =1. 25 16

Уравнения директрис:

	x = a	=	5	=	25	;	x = − a	= −	5	= −	25 .
			3		3				3
	ε						ε				3
			5						5

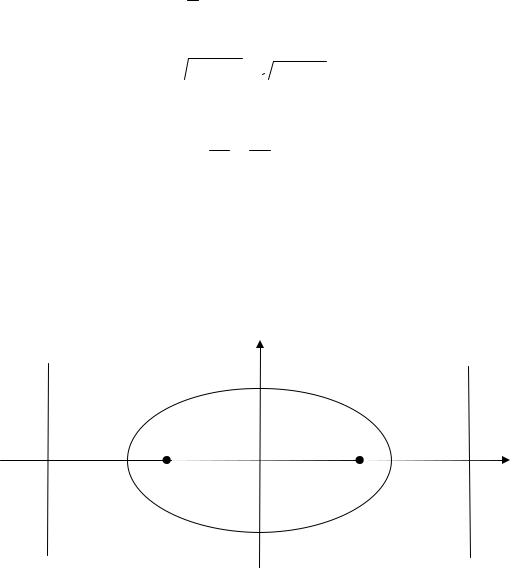
Эллипс и директрисы изображены на рис. 1.16.

y

x = −	25		B2	(0; 4)	x =	25
	3					3

A (−5; 0)		F1 (−3; 0)		O				A2 (5; 0)	x
						F (3; 0)
1						2

B1 (0; − 4)

Рис. 1.16

Задача 5. Фокусы гиперболы расположены на оси Ох симметрично началу координат. Записать уравнение гиперболы и сделать чертеж с изображением директрис и асимптот, если известно, что расстояние

между директрисами равно 12 54 , а уравнения асимптот y = ± 34 x .

35

Решение. Так как фокусы гиперболы расположены на оси Ох, то уравнение гиперболы имеет вид

	x2	−	y2	=1.
	a2		b2

Найдем а и b. Поскольку расстояние между директрисами равно

12 54 , то уравнение правой директрисы определяется выражением

x = a

=

32 . Учитывая то, что ε =

с

, c = a2 +b2 и

b

= 3

, имеем

a

a

ε

5

4

x =

a

=

a2

=

a2

=

a

=

a

=

4a

=

32

.

ε

c

a2 +b2

b 2

9

+1

5

5

+1

16

a

Следовательно, a =8, b = 6 , а уравнение гиперболы

x2

−

y2

=1.

64

36

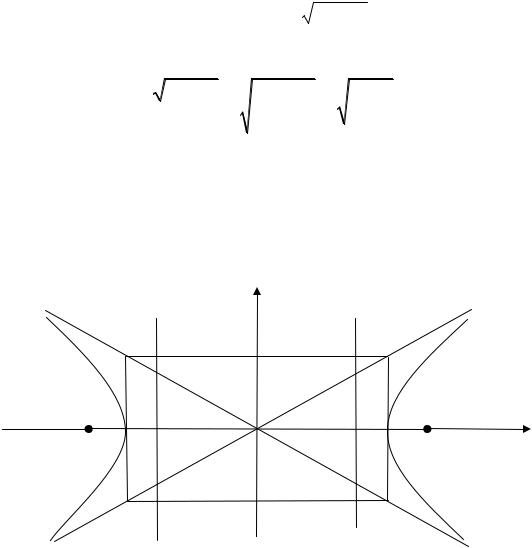
Искомая гипербола изображена на рис. 1.17.

y

x =

−

32

x =

32

5

5

B2 (0; 6)

A1 (−8; 0)

A2 (8; 0)

F1 (−10; 0)

F2 (10; 0)

x

O

B1 (0; − 6)

Рис. 1.17

Задача 6. Составить уравнение линии, каждая точка которой равноудалена от точки A(2; 2) и от оси абсцисс. Сделать чертеж.

36

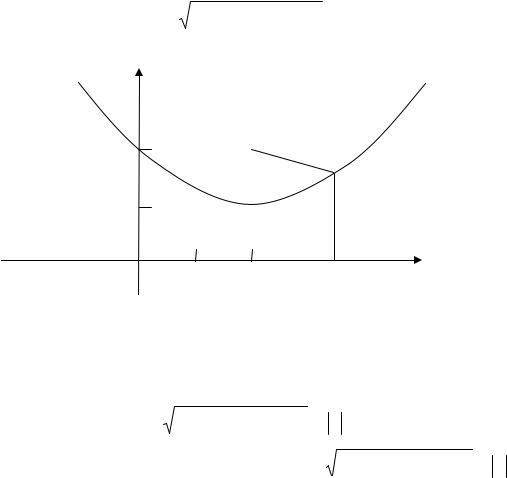
Решение. Пусть M (x; y) – произвольная точка искомой линии (рис.

1.18). Расстояние MA запишем в соответствии с формулами (1.10) и (1.11) в виде

MA = (x − 2)2 + (y − 2)2 .

y

•

2

A

M

1

B

O

1

2

N

x

Рис. 1.18

Расстояние от точки М до оси абсцисс, т. е. до точки N(x; 0), такое,

что MN Ox, составит:

MN = (x − x)2 + (y −0)2 = y .

Так как по условию задачи MA = MN , то

(x − 2)2 + (y − 2)2 = y ,

или, возведя обе части последнего уравнения в квадрат и выполнив тождественные преобразования, получим:

x2 − 4x + 4 + y2 − 4 y + 4 = y2 , т. е. y = 14 (x − 2)2 +1.

Последнее уравнение есть уравнение параболы, ветви которой направлены вверх, а вершина находится в точкеB(2;1).

37

x → a .

Тема 2. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

2.1.Понятие предела функции

иосновные теоремы о пределах

Множество точек, удовлетворяющих условию a < x < b , называется интервалом и обозначается (a; b) или ]a; b[ . Интервалы могут

быть конечными и бесконечными. Если один из концов интервала включается в множество, то множество называется полуинтервалом. Например, [a; b) .

Множество точек, удовлетворяющих условию a ≤ x ≤ b , называется отрезком и обозначается [a; b].

Окрестностью конечной точки x0 называется любой интервал, содержащий эту точку. Если из окрестности удалить точку x0 , то ок-

рестность называется проколотой.

Определение. Конечное число А называется пределом функции f (x) при x → a , если для любого ε > 0 существует такая проколотая

окрестность точки а, что для всех х из этой окрестности выполняется

неравенство f (x)− A < ε и записывается lim f (x) = A.

x→a

Введем понятие бесконечного предела функции при

Определение. Говорят, что lim f (x) = ∞, если для любого сколь

x→a

угодно большого числа M > 0 существует такая окрестность точки а,

что для всех х из этой окрестности выполняется неравенство f (x) > M .

Рассмотрим односторонние пределы. Если x → a и x < a, то это записывается в виде x → a −0 . Если же x → a и x > a, то это записывается в виде x → a + 0 . Числа

f (a −0) = lim f (x) и	f (a + 0) = lim f (x)
x→a −0	x→a +0

называют пределом слева функции f (x) в точке a и пределом справа функции f (x) в точке a (если эти числа существуют), соответственно.

Для существования предела f (x) при x → a необходимо и достаточно, чтобы имело место равенство f (a −0) = f (a + 0).

При вычислении пределов используют следующие основные теоремы о пределах.

38

Если существуют конечные пределы lim f (x) и lim g(x), то:
			x→a	x→a
1)	lim( f (x) + g(x)) = lim f (x) + lim g(x);
	x→a	x→a	x→a
2)	lim(	f (x) g(x) ) = lim f (x) lim g(x);
	x→a	x→a	x→a

		f (x)			lim f (x)
3)	lim			=	x→a		(если
					lim g(x)
	x→a g(x)
					x→a
4)	lim(c f (x)) = c lim f (x)
	x→a				x→a

lim g(x) ≠ 0 );

x→a

.

(2.1)

(2.2)

(2.3)

(2.4)

Для элементарных функций во всех точках из области их определения

lim f (x) = f (x0 ).

(2.5)

x→x0

Иногда полезно использовать равенства

))

x→a

(

ln f

(

x

))

= ln

(x→a

(

x

;

(2.6)

lim

lim f

lim f (x)

(2.7)

lim e f (x) = ex→a

.

x→a

Наконец, следует знать два замечательных предела:

1-й замечательный предел:

lim sin x

=1;

(2.8)

x→0

x

2-й замечательный предел:

lim 1+

1 x

1

lim(1 + α)

= e .

= e

, или

α

(2.9)

x→∞

x

α→0

Число e ≈ 2,718282

есть иррациональное число.

Логарифм по

основанию е называется натуральным логарифмом и записывается ln x , а функция y = ex называется экспонентой.

Поскольку lim f (x) = f (x0 ) (2.5), то при вычислении пределов,

x→x0

прежде всего, вместо x подставляем предельное значение (обычно это

39

записывается в квадратных скобках) и, если значение f ( x0 ) опреде-

лено, применяем основные теоремы о пределах.

Однако часто при подстановке в

f (x)

вместо x предельного зна-

0

;

;

[

0 ∞

]

;

[

∞ −∞

]

чения x получаются выражения вида:

0

∞

; 1∞

0

∞

и другие, которые называются неопределенностями. Полученные неопределенности нужно «раскрывать» специальными методами, учитывая характер стремления к пределу отдельных функций, составляющих данную функцию.

Рассмотрим основные приемы раскрытия некоторых видов неопределенностей.

1)При нахождении предела отношения двух многочленов при x → ∞, числитель и знаменатель дроби полезно разделить на xn , где n – наивысшая степень этих многочленов.

Задача 1. Вычислить lim

x

2 + 2x −10

.

x→∞ 3x2 − 5x +1

Решение. Вычислим данный предел:

2

10

lim

x2 + 2x −10

= ∞

= lim

1

+ x

− x2

=

1+ 0 −0 = 1 .

5 1

x→∞

3x

2

−5x +1

∞

x→∞

3 − 0 + 0 3

3

− x

+

x2

При решении задачи применили деление числителя и знаменателя

дроби на x2 и использовали соотношения (2.1)–(2.3).

Иногда аналогичный прием можно применить и для дробей, со-

	держащих иррациональности.				P(x)
	2) При нахождении предела lim						(а – конечное число) отно-
				x→a Q(x)
	шения двух многочленов P(x)			и Q(x) , где					P(a) = Q(a) = 0 , следует
	сократить дробь один или несколько раз на бином x − a .
	Задача 2. Вычислить lim		x2	−3x + 2		.
			x2	−7x +10
	x→2
	Решение. Используя формулу разложения квадратного трехчлена
	на множители ax2 +bx2 + c = a(x − x )(x − x							2	) , где x и	x – корни
				1					1	2

квадратного трехчлена, получим:

40