7

Замечания:

1.В частности, в неравенстве (2) за m1 можно взять наименьшее значение | f ¢(x)| при a < x < b.

2.Оценка (2) значительно завышена. Каждый из ниже рассматриваемых методов уточнения приближенного корня имеет свою оригинальную оценку.

3.Если e>0 – погрешность приближенного корня и |f( x )|< e, то не следует считать, что x является хорошим приближенным точного корня x, и, наоборот, если |f( x )|>e – полагать, что x есть грубое значение точного корня x. Более того, если уравнение f(x) = 0 умножить на произвольное число N ¹ 0, то получается равносильное уравнение Nf(x) = 0, причем число |Nf(x)| можно сделать сколь угодно большим или сколь угодно малым за счет выбора множителя N. На рис. 2 демонстрируется это утверждение.

y y

e f () e

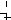
x x

xx

x

x

|f( x )| >e и |x – x | < e

|f( x )| < e и |x – x | >e

Рис. 2

1.2.3 Метод половинного деления

Для нахождения корня уравнения (1), принадлежащего отрезку [a; b], делим этот отрезок пополам. Если

æ	a +	b ö	= 0,
fç	2	÷
è		ø

то по определению

» 4,656613×10–10.

		8
	æ	a +	b ö
x = ç		2	÷
является корнем уравнения (1). Если	è		ø
	a +	b ö
æ			¹ 0,
fç	2	÷
è		ø

то выбираем ту из половин
é	a;	a +	bù	é	a + b	ù	,
ê		2	ú	или ê	2	; bú
ë			û	ë		û

исходного отрезка, на концах которых функция f(x) имеет противоположные знаки. Новый суженный отрезок [a1; b1] снова делим пополам и проводим то же рассмотрение. В результате получаем на каком-то этапе или точный корень x уравнения (1) или бесконечную последовательность вложенных друг в друга отрезков

[a1; b1], [a2; b2], ..., [an; bn], ...

таких, что

sgn f(an)× sgn f(bn) < 0

и			1
	bn – an =			(b – a).	(4)
			2n
Число x = liman	= limbn	является корнем уравнения (1).
n→ ∞	n→ ∞

Оценку погрешности на n-м шаге вычисления можно получить из следующих рассуждений: так как и точный корень x и срединная точка xn лежит на интервале [an; bn], то расстояние между ними не может быть больше половины длины этого интервала. Поэтому

	|x – xn| £	bn − an	для всех n.
		2

Объединив последний результат с результатом (4), получим

|x – xn| £	b − a	для всех n.	(5)
	2n+ 1

Достоинством метода деления пополам является то, что формула (5) дает предопределенную оценку точности вычисляемого решения. Например, если начальная длина интервала изоляции корня равна b – a = 2 и число повторяемых делений пополам равно 31, то в силу (5) ошибка ограничена значением

|e31| = 2232 = 2131

Можно показать, что n повторяемых делений пополам, необходимых для гарантии того, что n-я срединная точка xn является приближением к нулю функции и ошибка приближения меньше, чем наперед заданное значение e, равно

n =	é	ln( b -	a ) - ln( e	)ù	,	(6)
	ê		ln( 2 )	ú
	ë			û