9

где [ ] – операция взятия целой части числа.

1.2.3.1Алгоритм метода половинного деления

1.Ввести исходные данные: a, b – границы интервала изоляции корня уравнения (1); e – погрешность приближенного корня, . e >0; b > a.

2.Выполнить проверку применимости метода: если sgn f(a)×sgn f(b) > 0, то метод не применим; конец вычислений. Иначе выполнить 3.

3.Выполнить цикл пока b – a > e, т. е. длина отрезка изоляции корня больше

заданной точности e.

3.1. Вычислить x = (a + b)/2; x – срединная точка интервала [a;b] есть при-

ближение нуля f(x).

3.2. Если sgn f(x) = 0, то получено решение; выполнить выход из цикла.

Иначе	3.3. Если sgn f(x)= sgnf(a), то	принимаем a = x
	иначе принимаем b = x.
4.	Конец цикла.
5.	Вывод x – приближенного значения корня.
6.	Конец алгоритма.

1.2.4 Метод итераций
Заменим уравнение (1) равносильным уравнением
x = j(x).	(8)

Если любая точка x0 интервала [a; b] изоляции корня есть приближение нуля функции f(x), то следующее приближение получается так:

x1 = j(x0).

Подставляя теперь в правую часть последнего равенства вместо x0 число x1, получим новое число

x2 = j(x1).

Повторяя этот процесс, будем иметь последовательность чисел xn = j(xn–1) n = 1, 2, …

Если эта последовательность сходящаяся, т.е.

lim xn = ξ ,

n→ ∞

то, переходя к пределу в равенстве (9) и предполагая функцию ной, найдем:

nlim→ ∞ xn = j( nlim→ ∞ xn–1).

В силу (10) получаем

x = j(x),

(9)

(10)

ϕ (x) непрерыв-

10

т.е. в пределе значения аргумента и функции совпадают. Таким образом, предел ξ является корнем уравнения (1) и может быть вычислен по формуле (9) с любой степенью точности.

Достаточные условия сходимости итерационного процесса дает теорема 3.

Теорема 3. Пусть функция ϕ(x) определена и дифференцируема на отрезке [a; b], причем все ее значения ϕ(x) [a; b]. Тогда, если существует правильная дробь q такая, что

при a < x < b, то:

|ϕ ' (x) | ≤ q < 1

(11)

1) процесс итерации

(9) сходится независимо

от начального значения

x0 [a; b];

ξ = lim

2) предельное значение

xn

является единственным корнем уравне-

ния (1) на отрезке [a; b].

n→ ∞

Для оценки приближения используется формула

ξ − xn

≤

qn

x1 − x0

.

(12)

1 −

q

Если f(x) = x – ϕ(x), то оценку приближения можно выполнить по формуле

ξ − xn

≤

q

xn − xn-1

,

1

1 −

q

откуда, в частности, при q =

, получаем

2

|ξ – xn| ≤ |xn – xn–1|.

Из последнего неравенства следует, что, если |xn – xn–1| < ε, то и |ξ – xn| < ε.

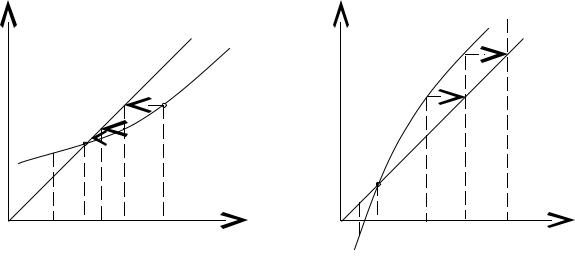
Метод итераций геометрически может быть пояснен следующим образом. Построим на плоскости xOy графики функций y = x и y = ϕ ( x ) . Каждый действительный корень ξ уравнения (8) является абсциссой точки М пересечения

кривой y =	ϕ ( x ) с прямой y = x (рис. 3).
Для	ϕ ′(x) > 0 и ϕ ′( x ) < 1 кривая y = ϕ ( x ) пересекает биссектрису y = x

(рис. 3а) слева направо и лежит под биссектрисой. Итерационный процесс, начи-

	ная с точки x0 монотонно сходится, приближаясь справа к ξ.
	В случае ϕ ′( x ) > 1 кривая	y = ϕ ( x ) находится над биссектрисой y = x ,
	пересекая ее слева направо, и процесс монотонно расходится (рис. 3б).
	y	y
	y=ϕ(x)	y=ϕ(x)	y=x
	y=x

M

	M
α ξ x2 x1 x0=β	α ξ x0=β x1 x2	x
а	б

11

Рис. 3. Геометрическая интерпретация итерационного процесса для уравнения x = ϕ ( x ) при ϕ ′( x ) > 0 .

В случае ϕ ′(x) < 0 кривые для ϕ ′(x) < 1 и ϕ ′(x) > 1 приведены на рис. 4 и

представляют соответственно сходящийся и расходящийся процессы с колебаниями вокруг истинного значения корня.

	y
y=x	y=ϕ(x)	y=x

y=ϕ(x)

α x1 ξ x2	x0=β	x	3	x ξ x	0	x	x
				1		б	2
	а

Рис. 4. Геометрическая интерпретация итерационного процесса

для уравнения x = ϕ ( x ) при ϕ ′( x )< 0: а) – для ϕ ′( x ) < 1; б) – для ϕ ′( x ) > 1 .

Уравнение (1) можно записать в виде равенства (8), выбирая различным образом функцию y = ϕ ( x ) . Для метода итераций выгодно то представление (8), при котором выполнено неравенство (11), причем, чем меньше q, тем быстрее, вообще говоря, последовательные приближения сходятся к корню (это следует из оценки приближения (12)).

Рассмотрим достаточно общий прием приведения уравнения (1) к виду (8),

для которого обеспечено выполнение неравенства (11). Пусть искомый корень ξ уравнения лежит на отрезке [a; b], причем, f '(x)>0 и

0 < m ≤ f '(x) ≤ M

(13)

при a ≤ x ≤ b. В частности, за m можно взять наименьшее значение производной f '(x) на отрезке [a; b], а за M – наибольшее значение f '(x) на отрезке [a; b]. Если производная f '(x) на отрезке [a; b] отрицательна, то вместо уравнения f(x) = 0 рассматриваем уравнение –f(x) = 0. Заменим уравнение (1) эквивалентным ему уравнением

12
x = x – λf(x), λ > 0.	(14)

Правая часть в полученном уравнении в соответствии с (8) есть функция

ϕ(x)= x – λf(x).

Тогда

ϕ '(x) = 1 – λf '(x).

Подберем параметр λ таким образом, чтобы на интервале [a; b] выполнялось неравенство (11), т.е.

0 ≤ ϕ '(x) = 1 – λf '(x) ≤ q < 1. Отсюда и на основании неравенства (13) получаем

0 ≤ 1 – λM ≤ 1 – λm ≤ q < 1.

Тогда, выбрав

	λ =	1	,	(15)
		M

получим

q = 1 – Mm < 1,

и неравенство (11) выполнено.

Замечания:

1.За число q в теореме 3 можно принять наименьшее значение модуля производной |ϕ ' (x)| при a < x < b.

2.В случае ϕ '(x) < 0 и |ϕ '(x)| < 1 имеет место неравенство

	ξ − xn		≤		xn − xn-1		.	(16)

3. В общем случае, из выполнения неравенства |xn – xn–1| < ε не следует выполнение неравенства |ξ – xn| < ε (см. рис.5).

y

	y=x
y=ϕ(x)
çξ-xnç	xn		xn-1
x		ε	x