
- •Самарская государственная академия путей сообщения
- •Рабочая программа
- •1. Линейная алгебра
- •2. Векторная алгебра и аналитическая геометрия
- •3. Комплексные числа
- •4. Введение в математический анализ
- •Рекомендуемая литература
- •Порядок выполнения и защиты контрольных работ по высшей математике
- •1. Задания для контрольной работы №1 Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •2. Методические указания к контрольной работе № 1
- •2.1. Линейная алгебра
- •Алгоритм построения обратной матрицы:
- •3. Решение типового варианта контрольной работы № 1
- •4. Задания для контрольной работы №2 Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •5. Методические указания к контрольной работе № 2
- •5.1. Аналитическая геометрия
- •5.2. Кривые второго порядка
- •6. Решение типового варианта контрольной работы № 2
- •7. Задания для контрольной работы №3 Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •Задание № 6
- •8. Методические указания к контрольной работе № 3
- •8.1. Комплексные числа
- •8.2. Введение в математический анализ
- •9. Решение типового варианта контрольной работы № 3
- •Библиографический список
- •Оглавление
- •Гуменникова Юлия Валерьевна
Задание № 4
Привести к каноническому виду уравнение
кривой второго порядка
![]() ,
определить тип линии и построить эту
кривую (табл. 4).
,
определить тип линии и построить эту
кривую (табл. 4).
Таблица 4
|
№ вари-анта |
Коэффициенты уравнений кривой |
№ вари-анта |
Коэффициенты уравнений кривой | ||||||||
|
A |
C |
D |
E |
F |
A |
C |
D |
E |
F | ||
|
9.1. |
1 |
1 |
–6 |
10 |
–15 |
9.16. |
4 |
4 |
–12 |
4 |
–3 |
|
9.2. |
1 |
4 |
0 |
–1 |
5 |
9.17. |
9 |
5 |
18 |
–30 |
9 |
|
9.3. |
2 |
0 |
8 |
–1 |
12 |
9.18. |
36 |
–4 |
–72 |
16 |
–88 |
|
9.4. |
9 |
4 |
–54 |
–32 |
109 |
9.19. |
–4 |
9 |
16 |
18 |
29 |
|
9.5. |
4 |
–9 |
–8 |
–36 |
–68 |
9.20. |
4 |
36 |
–16 |
72 |
–92 |
|
9.6. |
4 |
9 |
–40 |
36 |
100 |
9.21. |
9 |
4 |
54 |
8 |
49 |
|
9.7. |
9 |
–26 |
–54 |
–64 |
–127 |
9.22. |
1 |
4 |
–2 |
56 |
181 |
|
9.8. |
3 |
3 |
–24 |
12 |
58 |
9.23. |
7 |
–2 |
–42 |
–16 |
17 |
|
9.9. |
5 |
1 |
10 |
–6 |
–6 |
9.24. |
9 |
–4 |
0 |
24 |
–72 |
|
9.10. |
1 |
–1 |
6 |
0 |
8 |
9.25. |
–1 |
4 |
–4 |
8 |
–4 |
|
9.11. |
1 |
7 |
6 |
–28 |
–12 |
9.26. |
1 |
1 |
6 |
–4 |
0 |
|
9.12. |
3 |
–8 |
–6 |
–24 |
–36 |
9.27. |
1 |
1 |
–4 |
6 |
0 |
|
9.13. |
9 |
4 |
18 |
–8 |
–19 |
9.28. |
1 |
4 |
4 |
–16 |
–8 |
|
9.14. |
2 |
0 |
–4 |
–1 |
–4 |
9.29. |
1 |
–1 |
0 |
–4 |
0 |
|
9.15. |
9 |
–4 |
–36 |
–8 |
–4 |
9.30. |
25 |
9 |
–100 |
54 |
–44 |
Задание № 5
Даны уравнения линии в полярной системе координат. Требуется: 1) построить линию на промежутке от = 0 до= 2с шагом, равным; 2) найти уравнение линии в прямоугольной декартовой системе координат и назвать линию.
|
10.1.
|
10.2.
|
10.3.
|
|
10.4.
|
10.5.
|
10.6.
|
|
10.7.
|
10.8.
|
10.9.
|
|
10.10.
|
10.11.
|
10.12. |
|
10.13. |
10.14. |
10.15. |
|
10.16.
|
10.17.
|
10.18.
|
|
10.19.
|
10.20.
|
10.21. |
|
10.22.
|
10.23.
|
10.24.
|
|
10.25.
|
10.26.
|
10.27.
|
|
10.28.
|
10.29.
|
10.30.
|
5. Методические указания к контрольной работе № 2
5.1. Аналитическая геометрия
Выберем в
пространстве две упорядоченные точки
АиВ. Соответствующий направленный
отрезок![]() называетсявектором.
называетсявектором.
Расстояние между точками АиВназываетсямодулем илидлинойвектора.Для модуля вектора![]() используются обозначения
используются обозначения![]() ,а. Вектор
,а. Вектор![]() называетсяединичнымвектором,
если
называетсяединичнымвектором,
если![]() = 1.
= 1.
Несколько векторов называются
коллинеарными, если все они
расположены на прямых, параллельных
одной и той же прямой. Если векторы![]() и
и![]() коллинеарны, то записывают
коллинеарны, то записывают![]()
Несколько векторов называются компланарными,если существует плоскость, параллельная всем прямым, на которых эти векторы расположены.
Составим суммы векторов, умноженных на числа
![]()
Выражения такого вида называются линейными комбинациями векторов.
Если некоторый вектор представлен в виде линейной комбинации каких-либо векторов, то говорят, что он разложен по этим векторам.
Базисом в пространственазывают любые три упорядоченных некомпланарных вектора. При этом любой вектор пространства является их линейной комбинацией.
Если (![]() )
– базис в пространстве, то любой вектор
)
– базис в пространстве, то любой вектор
![]()
при этом
числа
![]() называютсякоординатамивектора
называютсякоординатамивектора![]() в базисе (
в базисе (![]() ).
Записывают
).
Записывают![]()
Выберем в пространстве точку Ои
возьмем упорядоченную тройку ортогональных
единичных векторов (![]() )
–базис в пространстве.
)
–базис в пространстве.
Совокупность точки Ои базиса (![]() )
называетсяортогональной декартовой
системой координат.При этом принята
следующая терминология:О –начало
координат; прямые, проходящие через
начало в направлении базисных векторов
–оси координат; плоскости, проходящие
через оси координат –координатные
плоскости. На
рис. 5.1 показана правая система координат.
)
называетсяортогональной декартовой
системой координат.При этом принята
следующая терминология:О –начало
координат; прямые, проходящие через
начало в направлении базисных векторов
–оси координат; плоскости, проходящие
через оси координат –координатные
плоскости. На
рис. 5.1 показана правая система координат.
Е
x b

![]()
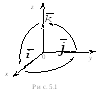 слиА(х1,у1, z1),B(х2,у2,
z2) – точки,
заданные в декартовой системе координат,
то координаты и модуль вектора
слиА(х1,у1, z1),B(х2,у2,
z2) – точки,
заданные в декартовой системе координат,
то координаты и модуль вектора![]() можно найти по формулам
можно найти по формулам
![]() , (5.1)
, (5.1)
![]() . (5.2)
. (5.2)
Скалярным произведениемдвух векторов называется число, равное произведению модулей векторов, умноженному на косинус угла между векторами
![]()
Если векторы заданы координатами, то скалярное произведение вычисляется по формуле
![]() 5.3)
5.3)
С помощью скалярного произведения можно найти угол между векторами через их координаты:
![]() (5.4)
(5.4)

 Векторным
произведением вектора
Векторным
произведением вектора![]() на вектор
на вектор![]() называется вектор
называется вектор![]() ,
модуль которого равен площади
параллелограмма, построенного на
векторах
,
модуль которого равен площади
параллелограмма, построенного на
векторах![]() и
и![]() ,
а направление ортогонально к векторам
,
а направление ортогонально к векторам![]() и
и![]() ,
причем векторы (
,
причем векторы (![]() )
образуют правую тройку векторов (рис.
5.2).
)
образуют правую тройку векторов (рис.
5.2).
![]() .
.
Обозначается векторное произведение
![]() .
.
Если векторы заданы координатами, то векторное произведение находится по формуле
 . (5.5)
. (5.5)
С помощью
векторного произведения можно вычислить
площадь треугольника
![]() ,
где
,
где![]() ,
,![]() –
векторы, на которых построен треугольник.
–
векторы, на которых построен треугольник.
Смешанное произведениетрех векторов определяется следующим образом:
![]()
Модуль смешанного произведения выражает объем параллелепипеда, построенного на перемножаемых векторах.
Если известны координаты векторов, то
 (5.6)
(5.6)
Линейное уравнение вида
![]() (5.7)
(5.7)
называется общим уравнением плоскости.
Вектор ![]() ,
составленный из коэффициентов при x,
y, z
, направлен по нормали к плоскости (5.7)
и называется нормальным
вектором плоскости.
,
составленный из коэффициентов при x,
y, z
, направлен по нормали к плоскости (5.7)
и называется нормальным
вектором плоскости.
Уравнение
плоскости, проходящей через данную
точку М(![]() )
имеет вид
)
имеет вид
![]() .
.
Уравнение
плоскости, проходящей через три точки
![]() ,
,![]() ,
,![]() ,
не лежащие на одной прямой, имеет вид
,
не лежащие на одной прямой, имеет вид
 . (5.8)
. (5.8)
Канонические уравнения прямой линии имеют вид
![]()
Здесь ![]()
некоторая фиксированная точка,
принадлежащая данной прямой;
некоторая фиксированная точка,
принадлежащая данной прямой; ![]()
направляющий вектор
прямой, т.е. вектор, лежащий на прямой,
параллельной данной.
направляющий вектор
прямой, т.е. вектор, лежащий на прямой,
параллельной данной.
Уравнение прямой,
проходящей через две точки ![]() ,
,
![]() ,
имеет вид
,
имеет вид
![]() . (5.9)
. (5.9)
Если точки
A(x1,y1,z1),B(x2,y2,z2)
иM(x,y,z)
лежат на одной прямой и![]() ,
то координаты точкиMможно найти по формулам
,
то координаты точкиMможно найти по формулам
![]() ;
;![]() ;
;![]() ,
,![]() . (5.10)
. (5.10)
Общее уравнение прямой на плоскостиимеет вид
![]() ,
,
причем хотя бы один из коэффициентов отличен от нуля.
Ненулевой
вектор
![]() = (А,В), перпендикулярный к данной
прямой, называетсянормальнымвекторомпрямой на плоскости.
= (А,В), перпендикулярный к данной
прямой, называетсянормальнымвекторомпрямой на плоскости.
Уравнение прямой на плоскости с угловым коэффициентомk имеет видy=kx + b(k=tg, где– угол наклона прямой к осиOх).
Условия параллельностииперпендикулярностидвух прямых с угловыми коэффициентамиk1иk2определяются соответственно равенствами
k1=k2,k1= –1 /k2.
Уравнение прямой, проходящей через точку М(х0,у0), параллельно данной прямойy=k2x + bимеет вид
![]() . (5.11)
. (5.11)
Уравнение прямой, проходящей через точку М(х0,у0), перпендикулярно данной прямойy=k1x + bимеет вид
![]() .
(5.12)
.
(5.12)
Расстояние d от точкиM(x0,y0) до прямойАх + Ву + С= 0 определяется по формуле
![]() . (5.13)
. (5.13)

 .
. .
.