5.2. Кривые второго порядка

Эллипсомназывается множество всех точек плоскости, для которых сумма расстояний от двух постоянных точек –фокусов, есть величина постоянная, равная 2а. Каноническое уравнение эллипса имеет вид

(5.14)

График эллипса симметричен относительно осей координат, а,b– полуоси эллипса (рис. 5.3). Точкии, где, называютсяфокусами эллипса. Числоназываетсяэксцентриситетомэллипса.

Если а > b, то прямыех=а/называютсядиректрисамиэллипса (еслиа < b, тодиректрисы определяются уравнениямиу=b/). Каждая директриса обладает следующим свойством: еслиr– расстояние от произвольной точки эллипса до некоторого фокуса,d– расстояние от той же точки до односторонней с этим фокусом директрисы, то отношениеr/dесть постоянная величина, равная эксцентриситету эллипса:r/d=.

Гиперболойназывается множество всех точек плоскости, для которых модуль разности расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная 2а. Каноническое уравнение гиперболы имеет вид

. (5.15)

График (рис. 5.4) симметричен относительно осей координат. Точки и, гденазываютсяфокусамигиперболы. Число–эксцентриситетгиперболы. Еслиа > b, то прямыех=а/называютсядиректрисамигиперболы.

Параболойназывается множество всех точек плоскости, равноотстоящих от данной точки, называемойфокусом, и данной прямой, называемойдиректрисой. Каноническое уравнение параболы имеет вид

(5.16)

График симметричен относительно оси(рис. 5.5).

Точка называетсяфокусом параболы. Прямаях= –р/ 2 называетсядиректрисой параболы. Считают, что для параболы.

Линия, которая в пространстве R²определяется уравнением

,

называется линией второго порядка.

После преобразования этого уравнения приходим к уравнению эллипса, гиперболы, параболы или вырожденной кривой.

Для определения положения точки на плоскости, кроме рассмотренной декартовой системы применяетсяполярная система координат. В этой системе любая точкаMфиксируется путем задания ее расстоянияrдо точкиOи угламежду осьюOx и вектором.При этом точкаOи осьOxвыбираются заранее, точкаOназываетсяполюсом,Ox–полярной осью,–полярным радиусомточкиM,–полярным угломточкиM. Записьозначает, что точкаMимеет координатыrи(рис. 5.5). В соответствии с определением.

Формулы, выражающие декартовы координаты точки через полярные, имеют вид

Формулы, позволяющие определить полярные координаты ипо декартовым координатамx,yточкиM, имеют вид

,

6. Решение типового варианта контрольной работы № 2

 Задание 1.По трем заданным точкамА(3, 1),В(–13, –11),С(–6, 13) построить треугольник и средствами векторной алгебры найти: 1) длину стороныВС; 2) уравнение линииВС; 3) уравнение высоты, проведенной из точкиА; 4) длину высоты, проведенной из точкиА; 5) площадь треугольникаАВС; 6) угол между сторонамиВАиВС; 7) координаты точкиN– середины стороныАС; 8) координаты точкиМ, делящей сторонуАВв отношении 2:3, считая от точкиА.

Решение. Чертеж треугольника приведен на рис. 6.1.

1. Вычислим координаты векторапо формуле (5.1)

= (–6–(–13); 13–(–11)) = (7, 24).

Вычислим длину вектора по (5.2)

= .

2. Запишем уравнение прямойВС в виде (5.9)

.

Уравнение прямой ВС:.

3. Уравнение высотыАDможет быть получено различными способами.

 способ. Заметим, что векторявляется нормальным вектором для прямойАDи точкаАпринадлежит прямойАD, следовательно,

.

Итак, АD:.

 способ. Запишем уравнение высоты, проведенной из точкиАв форме уравнения прямой с угловым коэффициентомk, при этом воспользуемся свойствами угловых коэффициентов взаимно перпендикулярных прямых.

Определим угловой коэффициент прямой ВС. Для этого разрешим уравнение прямой относительноу, имеем

.

Подставим полученные данные в (5.12) и получим

.

Запишем полученное уравнение в форме общего уравнения плоскости:

.

Заметим, что результаты в первом и втором слyчаях совпадают.

Итак, прямая АDзадается уравнением.

4. Длину высотыАDтакже можно определить различными способами.

 способ. Поскольку координаты точкиАизвестны, найдем координаты точкиD. Заметим, что точкаDлежит на пересечении прямыхВСиАD, следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Составляем систему из уравнений, задающих прямыеВСиАD:

Решим систему по формулам Крамера:

,

,,

;D(–8,52; 4,36).

Теперь воспользуемся формулой (5.2) для вычисления длины отрезка

.

 способ.Длину отрезкаАDможно рассматривать как расстояние от точкиА(3, 1) до прямойВС (), поэтому воспользуемся формулой (5.13)

.

5. Найти площадь треугольникаАВС.

В предыдущих пунктах были определены величина основания и длина высоты. Поэтому целесообразно применить формулу. Имеем(кв. ед.).

6. Для вычисления величины угла между сторонамиВАиВС(угол) воспользуемся формулой (5.4):

,,

.

.

 = аrcсos0,8 = 3650 (если воспользоваться калькулятором или компьютером, то результат может быть записан в виде 36,87).

7. Для нахождения координат середины отрезкаАСвоспользуемся формулой (5.10), где= 1. Имеем

.

8. Координаты точкиМ, найдем по формуле (5.10), где= 2 / 3:

;.

Окончательно: .

Ответ: = 25; уравнение прямойВС:; уравнение прямойАD:;;(кв. ед.); = 3650;;.

 Задание 2.По четырем заданным точкамА₁(4, 2, 5),А₂(0, 7, 2),А₃(0, 2, 7),А₄(1, 5, 0) построить пирамиду и средствами векторной алгебры найти: 1) длину ребраА₁А₂; 2) угол между ребрамиА₁А₂иА₁А₄; 3) площадь граниА₁А₂А₃; 4) объем пирамидыА₁А₂А₃А₄; 5) уравнение прямойА₁А₂; 6) уравнение плоскостиА₁А₂А₃.

Чертеж пирамиды приведен на рис. 6.2.

1. Найдем координаты и длину векторапо формулам (5.1), (5.2)

=,

.

2. Для определения угла, вычислим координаты и модули векторов, направленных по сторонам этого угла:

,;

.

Угол определим по формуле (5.4)

.

По таблицам находим .

3. Для вычисления площади граниА₁А₂А₃воспользуемся свойствами векторного произведения двух векторов, на которых построен треугольникА₁А₂А₃, и формулой (5.5):

,

= (–4, 5,–3),,

=

=,



(кв. ед.).

4. Для вычисления объема воспользуемся формулой смешанного произведения (5.6):

,

(куб. ед.).

5. Для определения уравнения прямойА₁А₂воспользуемся уравнением (5.9). Имеем

,

окончательно получаем уравнение прямой А₁А₂

.

6. Уравнение плоскостиА₁А₂А₃запишем в форме уравнения плоскости, проходящей через три точки (5.8)

.

Разделим обе части уравнения на 10, окончательно уравнение плоскости А₁А₂А₃примет видx+ 2y+ 2z – 18 = 0.

Ответ:;;(кв. ед.);(куб. ед.); уравнение прямойА₁А₂:; уравнение плоскостиА₁А₂А₃:x+ 2y+ 2z – 18 = 0.

Задание 3. Составить канонические уравнения:а) эллипса, зная, что расстояние между фокусами равно 8, а малая полуось равна 3;б) гиперболы, если она проходит через точку (–5, 3) и имеет эксцентриситет= 2;в) найти координаты фокуса и уравнение директрисы параболы .

Решение.

а). По условию, т.е.. Воспользуемся формулой, откуда:

или a = 5.

Тогда каноническое уравнение эллипса примет вид (5.14)

.

Выполним чертеж (рис. 6.3).

б

). Так как гипербола проходит через точку (–5, 3), то координаты этой точки удовлетворяют каноническому уравнению гиперболы (5.15), имеем

. (6.1)

По условию . Далее, используя формулу, получаем

.

Подставим последнее равенство в (6.1) и получим

.

Окончательно имеем:.

Получили равностороннюю гиперболу. Выполним чертеж (рис. 6.4).

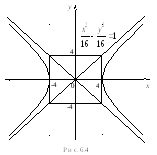
в). Из канонического уравнения параболы заключаем, что 2р= 8р= 4,р/ 2 = 2. Таким образом, уравнение директрисы запишется в видеу= –2, фокусом является точкаF(0, 2).

Выполним чертеж (рис. 6.5). 

Задание 4.Привести к каноническому виду уравнение кривой второго порядка, определить тип линии и построить эту кривую

.

Решение. Так как отсутствует член, содержащий произведениеху(В= 0), то поворота осей нет. Выделим полные квадраты. Для этого преобразуем уравнение

,

,

.

Сделаем перенос начала координат

тогда начало новой системы координат будет в точке , а уравнение примет вид. Преобразуем полученное уравнение и получим уравнение эллипса с полуосямиа= 3,b= 2:

.

Итак, в системе координатуравнение кривой принимает канонический вид. Оси координатипараллельны осям координатОхиОусоответственно, а начало перенесено в точку.

Используя полученные в процессе преобразования кривой данные, выполним построение кривой (рис. 6.6). 

Задание 5.Линия задана уравнениемв полярной системе координат. Требуется построить линию по точкам от= 0 до = 2с шагом/ 8. Найти уравнение данной линии в декартовой системе координат и назвать линию.

Решение. Составим табл. 5 для вычисления значенийr.

Таблица 5

	0	 / 8	 / 4	3 / 8	 / 2	5 / 8	3 / 4	7 / 8		…
r	1,5	1,52	1,58	1,67	1,8	1,95	2,096	2,21	2,25

Построим линию, учитывая, что (рис. 6.7).

Для перехода в декартовую систему координат воспользуемся формулами

,.

Получим уравнение

,

которое после преобразований примет вид





,



.

Получили уравнение эллипса с центром в точке О(–4; 0) и полуосямиа= 5,b= 3.