Полную группу можно определить так: если

для любой пары (i  j), тогда A₁, A₂, … , A_n - полная группа событий.

Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов.

Обозначим число благоприятствующих событию А исходов через М, а число всех исходов - N.

	(2.1)
где M - целое неотрицательное число, 0 M N

Другой тип объективной вероятности определяется исходя из относительной частоты (частости) появления события. Если, к примеру, некоторая фирма в течение времени провела опрос 1000 покупателей нового сорта напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток как 20/1000=0,02. В этом примере 20 - это частота наступления события, а 20/1000=0,02 - это относительная частота.

Относительной частотой события называется отношение числа испытаний m, при которых событие появилось, к общему числу проведенных испытаний n.

	(2.2)
где m - целое неотрицательное число, 0 m n

Статистической вероятностью события А называется относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний. Будем обозначать её Р^*(А). Следовательно,. При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. Р^* (A)  Р(A)

Для определения вероятности выпадения 1 или 2 при подбрасывании кости нам необходимо только знать “модель игры “, в данном случае - кость с 6 гранями. Мы можем определить наши шансы теоретически, без подбрасывания кости, это - априорная (доопытная) вероятность. Во втором примере мы можем определить вероятность только по результатам опыта, это - апостериорная (послеопытная) вероятность. То есть классическая вероятность - априорная, а статистическая - апостериорная.

Какой бы вид вероятности не был выбран для их вычисления и анализа используется один и тот же набор математических правил.

Свойства вероятности, вытекающие из классического определения.

1. Вероятность достоверного события равна 1, то есть Р() = 1.

Действительно, если событие А = , то M = N, значит Р() = N/N = 1.

2.Если событие невозможное, то его вероятность равна 0, то есть Р()= 0.

Если А = , то оно не осуществится ни при одном испытании, то есть M = 0 и Р() = 0/N = 0.

3.Вероятность случайного события есть положительное число, заключенное между 0 и 1.

В самом деле, та к как 0 M N , то 0 M/ N 1, то есть 0 Р(А) 1.

4. Сумма вероятностей противоположных событий равна 1, то есть . В самом деле,

А отсюда:

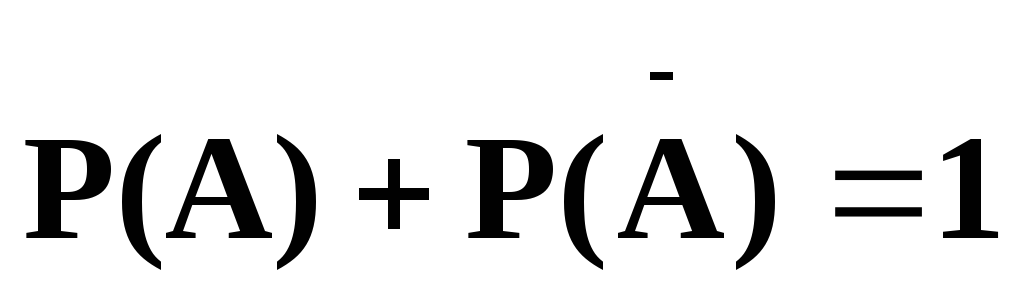
(2.3)

2.2. Правила сложения и умножения вероятностей. Зависимые и независимые события

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления, то есть:

Р (А+В) = Р(А) + Р(В) - Р(АВ)

или (2.4)

Для несовместных событий их совместное наступление есть невозможное событие , а вероятность его равна нулю. Следовательно, для несовместных событий правило сложения вероятностей принимает следующий вид:

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Для несовместных событий A, B:
или	(2.5)

Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, то есть:

P(A₁+A₂+A₃+...+A_n)=P(A₁)+P(A₂)+P(A₃)+...P(A_n)

или

(2.6)

В случае нескольких совместных событий необходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повторный учет областей пересечения событий. Рассмотрим три совместных события.

A	AB	B
	ABC
AC	C	CB

Рис. 2.3

Для случая трех совместных событий можно записать:

Р(А + В + С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС).

Сумма вероятностей событий А₁, А₂, А₃, ... , А_n, образующих полную группу, равна 1, то есть:

P(A₁) + P(A₂) + P(A₃) + ... + P(A_n) = 1

или

(2.7)

Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:

P(AB) = P(A)  P(B),
P(A B) = P(A) P(B)	(2.8)

или

События А₁, А₂, ..., A_n (n > 2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Распространим теоремы умножения на случаи n независимых и зависимых в совокупности событий.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

P(A₁ A₂A₃…A_n) = P(A₁) P(A₂)  P(A₃) … P(A_n) (2.9)

Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого:

	Р(АВ) = P(B)  Р(А/В)	(2.10)
	Р(АВ) = P(B)  Р(А/В)
	или Р(АВ) = P(A)Р(В/А)
	Р(АВ) = Р(A)(В/А)
Вероятность события В при условии появления события А:
P(B/A) = или P(B/A) =			(2.11)
.

Вероятность совместного наступления конечного числа n зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, т.е.

P(A1  A2  A3 ... Аn) = Р(A1)  P(A2 / A1) P(A3 / A1  A2). . . . P(An / A1  A2  A3 … An-1) ( 2.12)

Если события А₁, А₂, ... A_n - зависимые в совокупности, то вероятность наступления хотя бы одного из них соответственно равна:

(2.13)

Вероятность появления хотя бы одного события из n независимых в совокупности, равна разности между 1 и произведением вероятностей событий, противоположных данным, то есть:

(2.14)