2.5. Смешанное произведение трех векторов, его свойства, геометрический смысл, вычисление.

Определение:

(a x b)c – векторно-скалярное или смешанное произведение векторов.

1. Компланарность векторов a,b,c – принадлежность к одой плоскости или параллельным плоскостям. (можно снести на одну плоскость)

2. Упорядоченная тройка векторов, такая тройка векторов о которых известно, какой из них является первым, вторым и третьим.

3. Правая и левая тройка векторов.

x- вектор а

y- вектор b

z- вектор c

(a,b,c) (b,c,a) (c,a,b) правые

(b,a,c) (a,c,b) (c,b,a) левые

Теорема 1:

Смешанное произведение векторов (a x b)c равно объему параллелепипеда ( построенного на векторах a,b,c) взятому со знаком +, если тройка правая, и – если тройка левая.

Док-во:

Если a,b,c компланарны, то (a x b)c =0 (очевидно)

(a x b) |_c

Пусть a не коллинеарно b тогда a x b=Se (S- площадь параллелограмма)

(a,b , a x b,) – правая тройка

Se*c=S*|e|*пр_eс=S*пр_ec=S*H=V (если a,b,c – правая)

Если левая, то пр_ec=-H, (a x b)c=-V

Следствия:

1. (a x b)c=(b x c)a=a(b x c)=abc

2. Компланарность abc=0

Теорема 2:

Пусть a={x1,y1,z1} b={x2,y2,z2} c={x1,y1,z1} – векторы заданные декартовыми координатами. Тогда

|x1 y1 z1|

abc=|x2 y2 z2|

|x3 y3 z3|

Док-во:

abc=(a x b)c ↔ a x b=| i j k|=(y1z2-z1y2)i-(x1z2-x2z1)j+(x1y2-x2y1)k

|x1 y1 z1|

|x2 y2 z2|

abc – скалярное произведение (a x b) и с ↔ (a x b)c=x3(y1z2-z1y2)-y3(x1z2-x2z1)+z3(x1y2-x2y1)=| x1 y1 z1 |

|x2 y2 z2|

|x3 y3 z3|

3.1. Прямая линия на плоскости. Различные уравнения прямой. Угол между прямыми, условия параллельности и перпендикулярности прямых на плос­кости.

Нормальный и направляющий вектор прямой

Нормальный вектор прямой – любой ненулевой вектор, ортогональный этой прямой. n |_ L

Направляющий вектор прямой называется любой ненулевой вектор, параллельный этой прямой.

Определение:

Уравнение данной линии ( в выбранной системе координат) называется уравнением вида F(x,y)=0. Линия – геометрическое место точек удовлетворяющее этому уравнению.

Линия определяется уравнением y=f(x) – график функции f(x).

Векторное уравнение прямой на плоскости.

Составим общее векторное уравнение.

Очевидно, что MM0 |_ n, откуда скалярное произведение M0M*n=0, поскольку M0M=r-r0, то (r-r0)n=0, или rn-r0n=0.

Обозначив C=-r0n, получим rn+C=0 (общее векторное уравнение)

Составим векторное параметрическое уравнение:

Воспользуемся тем, что M0M||q или (r-r0)||q, откуда r-r0=tq (векторное параметрическое уравнение прямой а плоскости)

Общее уравнение прямой на плоскости:

Теорема:

В декартовой системе координат каждая прямая определяется уравнением первой степени.

Док-во:

(y-b)/x=k=tgα

(y-b)/x=k → y-b=kx → kx-y+b=0 уравнение первой степени.

Если α=90 → x=a также уравнение первой степени.

Общее уравнение прямой на плоскости:

Ax+By+C=0

Неполное уравнение первой степени:

а) С=0 → Ax+By=0 – уравнение прямой проходящей через начало координат.

б) A=0 → By+C=0 → y=-C/B

B≠0 (прямая параллельная оси Ох)

в) B=0 → Ax+C=0 → x=-C/A (прямая параллельная оси Ох)

Уравнение прямой в отрезках:

Ax+By+C=0 → Ax+By=-C → -Ax/C-By/C=1 → x/-CA+y/-CB=1 → x/a+y/b=1 (2)

(2) уравнение прямой в отрезках.

a,b – отрезки, отсекаемые прямой на координатных осях ( не длины отрезков)

Каноническое уравнение прямой на плоскости. (типовое, традиционное)

Задача:

Найти уравнение прямо проходящей через заданную точку М1(x1,y1) и имеющий заданный направляющий вектор q.

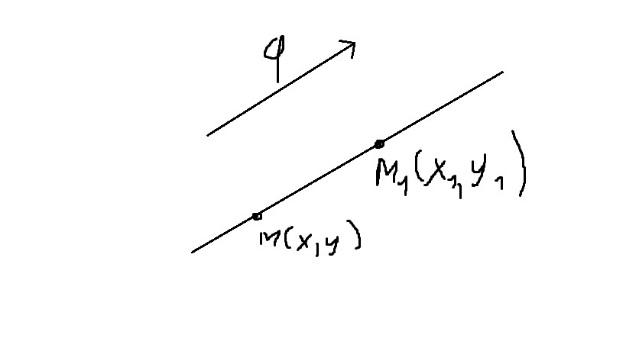
q={q1,q2}

MM1={x-x1,y-y1}

MM1||q → (x-x1)/q1=(y-y1)/q (6) уравнение канонической прямой

Если в (6) в знаменателе 0, то в числителе также 0.

Параметрическое уравнение прямой:

(x-x1)/q1=(y-y1)/q2 → (x-x1)/q1=t (y-y1)/q2=t → x=x1+q1*t

y=y1+q2*t

(7) параметрическое уравнение прямой.

Уравнение прямой проходящей через 2е заданные точки.

M1(x1,y1) M2(x2,y2)

M1M2={x2-x1,y2-y1}=q → (x-x1)/(x2-x1)=(y-y1)/(y2-y1)

Векторное уравнение прямой

L: Ax+By+C=0

Ax0+By0+C=0 ↔ M0(x0,y0) принадлежит L

A(x-x0)+B(y-y0)=0 ↔ n |_ τ

n{A,B} τ{x-x0,y-y0}

→ n-нормаль к L (вектор нормали)

→ n*τ=0 (9) векторное уравнение прямой.

Уравнение прямой с угловым коэффициентом:

L1: y=k1x+b1

L2: y=k2x+b2

tgα1=k1

tgα2=k2

φ=α2-α1

tgφ=tg(α2-α1)=(tgα2-tgα1)/(1+tgα1*tgα2)=(k2-k1)/(1+k1*k2)

а) Если поменять α1 и α2 местами, то изменится знак (мы рассматриваем один из смежных углов)

б) Ортогональность φ=π/2 → tgα1*tgα2=-1 → tgα1=-1/tgα2

в) Уравнение прямой проходящей через заданную точку с заданным угловым коэффициентом y-y0=k(x-x0)

Угол между двумя прямыми:

а) Общие уравнения:

L1:A1x+B1y+C1=0 | n1={A1,B1}

L2:A2x+B2y+C2=0 | n2={A2,B2}

φ=угол между(n1,n2) → cosφ=(n1*n2)/(|n1|*|n2|)=(A1A2+B1B2)/(√(A²1+B²1)+√( A²2+B²2))

б) Прямые заданы канонически:

L1: (x-x1)/l1=(y-y1)/m1 |q1={l1,m1}

L2: (x-x2)/l2=(y-y2)/m2 |q2={l2,m2}направляющие векторы

cosφ=(q1*q2)/(|q1|*|q2|=(l1l2+m1m2)/(√(l²1+m²1)+√( l²2+m²2))

Условие параллельности:

Если прямые параллельны, то их нормальные векторы, а также их направляющие векторы коллинеарны. Поэтому координаты этих векторов пропорциональны

n1||n2 → A1/A2=B1/B2

q1||q2 →l1/l2 =m1/m2

k1=k2

Условие перпендикулярности:

Если прямые перпендикулярны, то их направляющие векторы ортогональны

n1 |_n2 →n1*n2=0 A1A2+B1B2=0

q1 |_ q2 →q1*q2=0 l1*l2+m1*m2=0

k1*k2=0

Нормальное Уравнение

n |_ L; P – точка пересечения

p=|OP| расстояние от начала координат до прямой. Положительное направление нормали – как на рисунке ( исходит из начала координат и пересекает L)

Если L проходит через начало координат, то не определено положение направления.

p и α известны, запишем уравнение L

Полярные координаты:

ρ=√(X²m+Y²m) Xm= ρcosβ; Ym= ρsinβ

пр_nОМ=p= ρsinα*sinβ=(ρcosβ)cosα+(ρsinβ)sinα=Xm*cosα+Ym*sinα → X*cosα+Y*sinα=0 (19) Нормальное уравнение плоскости.

Теорема:

Если точка M*(x*,y*), а прямая L – задана уравнением X*cosα+Y*sinα=0, то

δ=(x*)*cosα+(y*)*sinα-p (20)

Док-во:

пр_nОМ*=(x*)*cosα+(y*)*cos(90-α)= (x*)*cosα+(y*)*sinα → δ=(x*)*cosα+(y*)*sinα-p

δ(M*,L)=|δ|

Приведение уравнения прямой к нормальному виду:

Ax+By+C=0 – общее уравнение

xcosα+ysinα-p=0 –нормальное уравнение

cosα/А=sinα/В=-Р/С=μ

μ – нормирующий множитель =сonst