10.4. Екстремум функції двох змінних

10.4.1. Основні поняття

Поняття максимуму, мінімуму, екстремуму функції двох змінних аналогічні відповідним поняттям функції однієї незалежної змінної (див. п. 25.4).

Нехай функція визначена в деякій області , точка

Точка називаєтьсяточкою максимуму функції якщо існує такий – окіл точки, що для кожної точки , відмінної від, з цього околу виконується нерівність.

Аналогічно визначається точка мінімуму функції: для всіх точок ,відмінних від,із– околу точки виконується нерівність:.

На рисунку 5: – точка максимуму, – точка мінімуму функції .

Значення функції в точці максимуму (мінімуму) називається максимумом (мінімумом) функції. Максимум і мінімум функції називають її екстремумами.

Відзначимо, що, за означенням, точка екстремуму функції лежить всередині області визначення функції; максимум і мінімум мають локальний (місцевий) характер: значення функції в точці порівнюється з її значеннями в точкахдостатньо близьких до 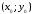. В областіфункція може мати декілька екстремумів або не мати жодного.

Рис. 5

10.4.2. Необхідні і достатні умови екстремуму

Розглянемо умови існування екстремуму функції.

Теорема 10.4.1. (необхідні умови екстремуму). Якщо в точці диференційовна функція має екстремум, то її частинні похідні в цій точці рівні нулю: , .

Зафіксуємо одну із змінних. Покладемо, наприклад . Тоді отримаємо функцію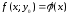однієї змінної, яка має екстремум при. Отже, згідно необхідній умові екстремуму функції однієї змінної (див. п. 25.4), 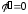, тобто .

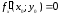Аналогічно можна показати, що .

Геометрично рівності і означають, що в точці екстремуму функції дотична площина до поверхні, що зображає функцію, паралельна площині, так як рівняння дотичної площини(див. формулу (3.2)).

Зауваження. Функція може мати екстремум в точках, де хоча б одна з частинних похідних не існує.

Наприклад, функція має максимум в точці(див. рис. 6), але не має в цій точці частинних похідних.

Точка, в якій частинні похідні порядку функції рівні нулю, тобто, ,, називається стаціонарною точкою функції .

Стаціонарні точки і точки, в яких хоча б одна частинна похідна не існує, називаються критичними точками. Рис.6

В критичних точках функція може мати екстремум, а може і не мати. Рівність нулю частинних похідних є необхідною, але не достатньою умовою існування екстремуму. Розглянемо, наприклад, функцію . Для неї точкає критичною (в ній і перетворюються в нуль). Проте екстремуму, в ній функція не має, так як в достатньо малому околі точкизнайдуться точки для яких(точки І і III четвертей) і(точки II і IV четвертей).

Таким чином, для знаходження екстремумів функції в даній області необхідно кожну критичну точку функції піддати додатковому дослідженню.

Теорема 10.4.2. (достатня умова екстремуму). Нехай в стаціонарній точці деякого її околу функція має неперервні частинні похідні до другого порядку включно. Обчислимо в точці значення ,

Позначимо

Тоді:

1. якщо , то функціяв точцімає екстремум:

максимум, якщо ;

мінімум, якщо ;

2. якщо , то функція в точці екстремуму не має.

У випадку екстремум вточці може бути, може не бути. Необхідні додаткові дослідження.

Приймемо без доведення.

Приклад 1. Знайти екстремум функції .

 Тут Точки, в яких частинні похідні не існують, відсутні.

Знайдемо стаціонарні точки, розв’язуючи систему рівнянь:

Звідси одержуємо точки і

Знаходимо частинні похідні другого порядку даної функції:

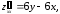
В точці маємо:, звідситобто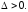

Оскільки , то в точці функція має локальний максимум

В точці :і, значить. Проведемо додаткове дослідження. Значення функціїв точцірівне нулю: . Можна помітити, що при,при , . Значить, в околі точки 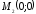функціяприймає як негативні, так і позитивні значення. Отже в точці функція екстремуму не має.