
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
Нехай
функція
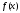 неперервна на проміжку
неперервна на проміжку
![]() і має нескінченний розрив при
і має нескінченний розрив при
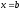 .
Якщо існує скінчена границя
.
Якщо існує скінчена границя
 ,
то її називають невласним
інтегралом другого роду
і
позначають
,
то її називають невласним
інтегралом другого роду
і
позначають
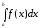 .
.
Таким чином, за означенням
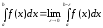 .
.
Якщо
границя в правій частині існує, то
невласний інтеграл
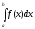 збіжний.
Якщо ж вказана границя не існує або
нескінченна, то говорять, що інтеграл
збіжний.
Якщо ж вказана границя не існує або
нескінченна, то говорять, що інтеграл
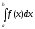 розбіжний.
розбіжний.
Аналогічно,
якщо функція
 має нескінченний розрив в точці
має нескінченний розрив в точці
 ,
то вважають
,
то вважають
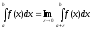 .
.
Якщо
функція
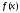 має розрив у внутрішній точці
має розрив у внутрішній точці
 відрізка
відрізка
![]() ,
то невласний інтеграл другого роду
визначається формулою
,
то невласний інтеграл другого роду
визначається формулою
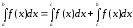 .
.
В цьому випадку інтеграл зліва називають тим, що збіжний, якщо обидва невласні інтеграли, що стоять справа, сходяться.
У
разі, коли
 ,
невласний інтеграл другого роду
,
невласний інтеграл другого роду
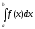 (розрив в точці
(розрив в точці
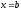 )
можна використовувати геометрично як
площу нескінченно високої криволінійної
трапеції (див. рис. 173).
)
можна використовувати геометрично як
площу нескінченно високої криволінійної
трапеції (див. рис. 173).

(рис.173)
Приклад
9.6.4.
Обчислити
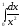 .
.
○
При
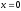 функція
функція
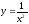 має нескінченний розрив;
має нескінченний розрив;
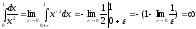 ,
інтеграл розбіжний. ●
,
інтеграл розбіжний. ●
Сформулюємо ознаки для невласних інтегралів другого роду.
Теорема
9.6.3.
Нехай
на проміжку
![]() функції
функції
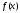 і
і
 неперервні при
неперервні при
 мають нескінченний розрив і задовольняють
умову
мають нескінченний розрив і задовольняють
умову
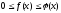 .
.
Із
збіжності інтеграла
 витікає збіжність інтеграла
витікає збіжність інтеграла ,
а з розбіжності інтеграла
,
а з розбіжності інтеграла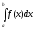 витікає розбіжність інтеграла
витікає розбіжність інтеграла .
.
Теорема
9.6.4.
Нехай
функції
 і
і
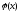 неперервні на проміжку
неперервні на проміжку
 і в точці
і в точці
 мають розрив. Якщо існує границя
мають розрив. Якщо існує границя
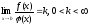 ,
то інтеграли
,
то інтеграли
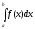 і
і
 одночасно сходяться або розходяться.
одночасно сходяться або розходяться.
Приклад 9.6.5. Чи збіжний інтеграл
○
Функція
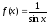 має на
має на
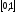 єдиний розрив в точці
єдиний розрив в точці
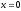 .
Розглянемо функцію
.
Розглянемо функцію
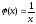 .
Інтеграл
.
Інтеграл
 розбіжний. І оскільки
розбіжний. І оскільки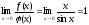 ,
то інтеграл
,
то інтеграл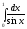 також розбіжний. ●
також розбіжний. ●
Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
9.7.1. Схеми застосування визначеного інтеграла
Нехай
вимагається знайти значення якої-небудь
геометричної або фізичної величини А
(площа фігури, об'єм тіла, тиск рідини
на вертикальну пластину і т.д.), пов'язаної
з відрізком
![]() зміни незалежної змінної
зміни незалежної змінної .
Вважається, що ця величина А адитивна,
тобто така, що при розбитті відрізка
.
Вважається, що ця величина А адитивна,
тобто така, що при розбитті відрізка![]() точкою
точкою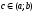 на частини
на частини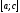 і
і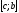 значення величини А, відповідає всьому
відрізку
значення величини А, відповідає всьому
відрізку![]() ,
рівне сумі її значень, відповідних
,
рівне сумі її значень, відповідних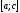 і
і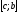 .Для
знаходження цієї величини А можна
керуватися однією з двох схем: перша
схема (або метод інтегральних сум) і
друга схема (або метод диференціала).Перша
схема базується на означенні визначеного
інтеграла.
.Для
знаходження цієї величини А можна
керуватися однією з двох схем: перша
схема (або метод інтегральних сум) і
друга схема (або метод диференціала).Перша
схема базується на означенні визначеного
інтеграла.
Точками
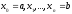 розбити відрізок
розбити відрізок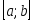 на
на
 частин.
Відповідно до цього величина А, яка
цікавить нас, розіб'ється на
частин.
Відповідно до цього величина А, яка
цікавить нас, розіб'ється на
 «елементарних доданків»
«елементарних доданків»
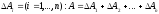 .
.Подати кожний «елементарний доданок» у вигляді добутку деякої функції (визначуваної з умови задачі), обчисленої в довільній точці відповідного відрізка на його довжину:
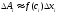 .
.
При
знаходженні наближеного значення
 допустимі деякі спрощення:
допустимі деякі спрощення:
дугу на елементарній ділянці можна замінити хордою, що стягує її кінці; змінну швидкість на елементарній ділянці можна приблизно вважати постійною і т.д.
Отримаємо наближене значення величини А у вигляді інтегральної суми:
 .
.
Шукана величина А дорівнює границі інтегральної суми, тобто
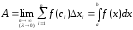 .
.
Вказаний «метод сум», як бачимо, заснований на поданні інтеграла як суми нескінченно великого числа нескінченно малих доданків.
Перша схема бала застосована для з'ясування геометричного і фізичного змісту визначеного інтеграла.
Друга схема є дещо видозміненою першою схемою і називається «метод диференціала» або «метод відкидання нескінченно малих вищих порядків»:
На відрізку
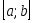 вибираємо довільне значення
вибираємо довільне значення
 і розглядаємо
і розглядаємо
змінний
відрізок
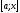 .
На цьому відрізку величина А стає
функцією
.
На цьому відрізку величина А стає
функцією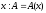 ,
тобто вважаємо, що частина шуканої
величини А є невідомою функцією
,
тобто вважаємо, що частина шуканої
величини А є невідомою функцією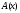 ,
де
,
де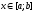 —
один з параметрів величини А;
—
один з параметрів величини А;
Знаходимо головну частину приросту
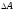 при зміні
при зміні
 на малу
на малу
величину
 ,
тобто знаходимо диференціал
,
тобто знаходимо диференціал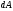 функції
функції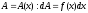 ,
де
,
де ,
визначена з умови задачі, функція змінної
,
визначена з умови задачі, функція змінної (тут також можливі різні спрощення);
(тут також можливі різні спрощення);
Вважаючи, що
 ,
знаходимо шукану величину шляхом
,
знаходимо шукану величину шляхом
інтегрування
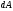 в межах від
в межах від
 до
до
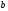 :
:
 .
.
