
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
Приклад 9.7.9. Дано циклоїда
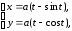
 .
.
Знайти
площу поверхні, утвореної обертанням
її навколо осі
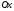 .
.
○ При
обертанні половини
дуги циклоїди навколо осі
 площа поверхні обертання дорівнює
площа поверхні обертання дорівнює

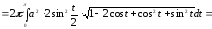

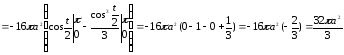 ,
,
тобто
 .
Отже,
.
Отже,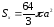 .
●
.
●
9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
Нехай
матеріальна точка
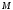 переміщується вздовж осі
переміщується вздовж осі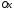 під дією змінної сили
під дією змінної сили ,
направленої паралельно цій осі. Робота,
виконана силою при переміщенні точки
,
направленої паралельно цій осі. Робота,
виконана силою при переміщенні точки
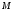 з положення
з положення
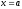 в положення
в положення
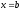 ,
,
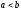 ,
знаходиться по формулі
,
знаходиться по формулі
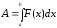 (9.7.10)
(9.7.10)
Приклад 9.7.10. Яку роботу потрібно затратити, щоб розтягнути пружину на 0,05 м, якщо сила 100 H розтягує пружину на 0,01 м?
○ За
законом Гука пружна сила, що розтягує
пружину, пропорційна видовженню
 ,
тобто
,
тобто
 ,
де
,
де
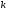 —коефіцієнт
пропорційності. Згідно з умовою задачі,
сила
—коефіцієнт
пропорційності. Згідно з умовою задачі,
сила
 розтягує пружину на
розтягує пружину на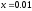 м;
отже,
м;
отже,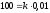 ,
звідси
,
звідси ;
отже,
;
отже,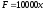 .
.
Шукана робота за формулою (9.7.10) дорівнює
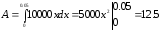 (Дж).
●
(Дж).
●
Приклад
9.7.11.
Знайти
роботу, яку необхідно затратити, щоб
викачати через край рідину з вертикального
циліндрового резервуару висоти
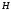 м
і радіусом основи
м
і радіусом основи
 м.
м.
○ Робота,
затрачена на підняття тіла вагою
 на висоту
на висоту
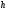 ,
дорівнює
,
дорівнює
 .
Але різні шари рідини в резервуарі
знаходяться на різних глибинах і висота
підняття (до краю резервуару) різних
шарів не однакова.
.
Але різні шари рідини в резервуарі
знаходяться на різних глибинах і висота
підняття (до краю резервуару) різних
шарів не однакова.
Для розв’язку поставленої задачі застосуємо другу схему (метод диференціала). Введемо систему координат так, як показано на рис. 193.

(рис.193)
Робота, затрачена на викачування з резервуару шару рідини товщиною
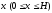 ,
є функція від
,
є функція від
 ,
тобто
,
тобто
 ,
де
,
де
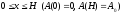 .
.
Знаходимо головну частину приросту
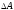 при зміні
при зміні
 на величину
на величину
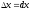 ,
,
тобто
знаходимо диференціал
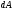 функції
функції
 .
.
Зважаючи
на невеликий
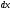 вважаємо, що «елементарний» шар рідини
знаходиться на одній глибині
вважаємо, що «елементарний» шар рідини
знаходиться на одній глибині
 (від
краю резервуару) (див. рис. 193). Тоді
(від
краю резервуару) (див. рис. 193). Тоді
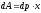 ,
де
,
де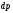 —
вага цього шару; він дорівнює
—
вага цього шару; він дорівнює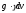 ,
де
,
де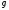 —
прискорення вільного падіння,
—
прискорення вільного падіння,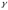 —
густина рідини,
—
густина рідини, —
об’єм «елементарного» шару рідини (на
рис. він виділений), тобто
—
об’єм «елементарного» шару рідини (на
рис. він виділений), тобто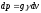 .
Об'єм вказаного шару рідини, очевидно,
дорівнює
.
Об'єм вказаного шару рідини, очевидно,
дорівнює
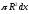 ,
де
,
де
 —висота
циліндра (шару),
—висота
циліндра (шару),
 —
площа його основи, тобто
—
площа його основи, тобто
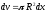 .
.
Таким
чином,
 і
і
 .
.
Інтегруючи отриману рівність в межах від
 до
до
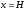 ,
знайдемо, що
,
знайдемо, що
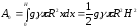 (Дж).
●
(Дж).
●
Шлях, пройдений тілом.
Нехай матеріальна точка переміщується по прямій із змінною швидкістю
 .
Знайдемо шлях, пройдений нею за проміжок
часу від
.
Знайдемо шлях, пройдений нею за проміжок
часу від
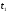 до
до
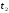 .
.
Розв’язання:
З фізичного змісту похідної відомо, що
при русі точки в одному напрямі «швидкість
прямолінійного руху дорівнює похідній
від шляху по часу», тобто
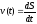 .
Звідси випливає, що
.
Звідси випливає, що
 .
Інтегруючи отриману рівність в межах
від
.
Інтегруючи отриману рівність в межах
від
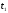 до
до
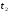 ,
отримаємо
,
отримаємо
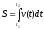 .
.
Відзначимо, що цю ж формулу можна отримати, користуючись схемою І або ІІ застосування визначеного інтеграла.
Приклад
9.7.12.
Знайти
шлях, пройдений тілом за 4 секунди від
початку руху, якщо швидкість тіла
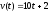 (м/с).
(м/с).
○
Якщо
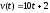 (м/с),
то шлях, пройдений тілом від початку
руху
(м/с),
то шлях, пройдений тілом від початку
руху
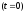 до кінця 4-ої секунди, дорівнює
до кінця 4-ої секунди, дорівнює
 (м).
●
(м).
●
Тиск рідини на вертикальну пластинку
За
законом Паскаля тиск рідини на
горизонтальну пластинку дорівнює вазі
стовпа цієї рідини, що має основою
пластинку, а висотою—глибину її занурення
від вільної поверхні рідини, тобто
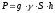 ,
де
,
де
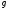 —
прискорення вільного падіння,
—
прискорення вільного падіння, —
густина рідини,
—
густина рідини, —
площа пластинки,
—
площа пластинки, —
глибина її занурення.
—
глибина її занурення.
По цій формулі не можна знаходити тиск рідини на вертикально занурену пластинку, оскільки її різні точки лежать на різних глибинах.
Нехай
в рідину занурена вертикально пластина,
обмежена лініями
 ;
система координат вибрана так, як це
показано на рис. 194. Для знаходження
тиску
;
система координат вибрана так, як це
показано на рис. 194. Для знаходження
тиску
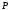 рідини на цю пластину застосуємо схему
ІІ
(метод диференціала).
рідини на цю пластину застосуємо схему
ІІ
(метод диференціала).
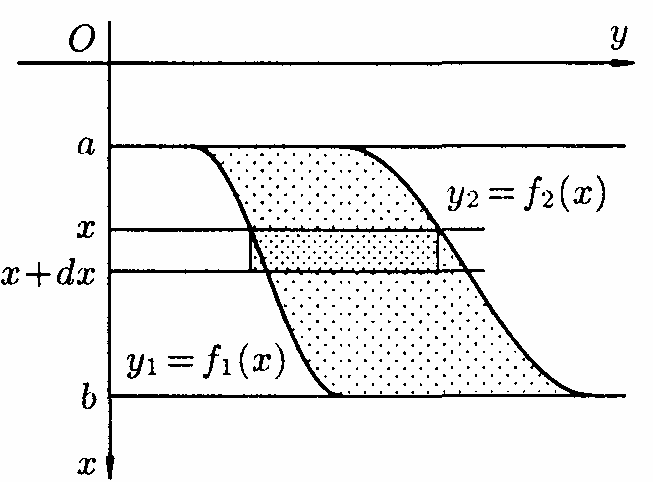
(рис.194)
Нехай частина шуканої величини
 є функція від
є функція від
 ,
тобто
,
тобто
 —
тиск на частину пластини, відповідне
відрізку
—
тиск на частину пластини, відповідне
відрізку
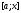 значень змінної
значень змінної
 ,
де
,
де
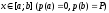 .
.Дамо аргументу
 приріст
приріст
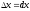 .
Функція
.
Функція
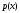 отримає приріст
отримає приріст
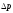
(на
рис. — полоска товщини
 ).
Знайдемо диференціал
).
Знайдемо диференціал
 цієї функції. Зважаючи на невеликий
цієї функції. Зважаючи на невеликий
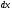 приблизно вважатимемо смужку прямокутником,
всі
точки якого знаходяться на одній глибині
приблизно вважатимемо смужку прямокутником,
всі
точки якого знаходяться на одній глибині
 ,
тобто
пластинка ця — горизонтальна.
,
тобто
пластинка ця — горизонтальна.
Тоді
за законом Паскаля
 .
.
Інтегруючи отриману рівність в межах від
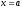 до
до
 ,
отримаємо
,
отримаємо
 або
або  .
.
Приклад
9.7.13.
Визначити
величину тиску води на півколо, вертикально
занурене в рідину, якщо його радіус
 ,
а центр
,
а центр
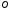 знаходиться на вільній поверхні води
(див. рис. 195).
знаходиться на вільній поверхні води
(див. рис. 195).
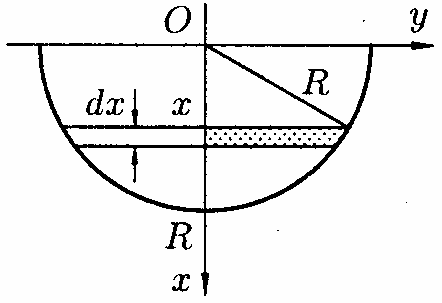
(рис.195)
○ Скористаємося
отриманою формулою для знаходження
тиску рідини на вертикальну пластинку.
В даному випадку пластинка обмежена
лініями
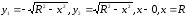 .
Тому
.
Тому
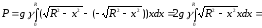
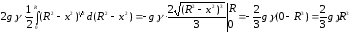 .
●
.
●
Обчислення статичних моментів і координат центру ваги плоскої кривої
Нехай
на площині
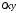 задана система матеріальних точок
задана система матеріальних точок
 відповідно з масами
відповідно з масами
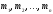 .
.
Статичним
моментом
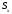 системи
матеріальних точок відносно осі
системи
матеріальних точок відносно осі
 називається сума добутків мас цих точок
на їх ординати (тобто на відстані цих
точок від осі
називається сума добутків мас цих точок
на їх ординати (тобто на відстані цих
точок від осі
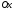 ):
):
 .
.
Аналогічно
визначається статичний момент
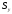 цієї
системи відносно осі
цієї
системи відносно осі
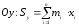 .
.
Якщо маси розподілені неперервним чином вздовж деякої кривої, то для виразу статичного моменту знадобиться інтеграція.
Нехай
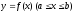 — це рівняння матеріальної кривої
— це рівняння матеріальної кривої
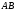 .
Вважатимемо її однорідною з постійною
лінійною густиною
.
Вважатимемо її однорідною з постійною
лінійною густиною
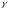
 .
.
Для
довільного
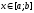 на кривій
на кривій
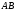 знайдеться точка з координатами
знайдеться точка з координатами
 .
.
Виділимо
на кривій елементарну ділянку довжини
 ,
що містить точку
,
що містить точку
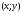 .
Тоді маса цієї ділянки дорівнює
.
Тоді маса цієї ділянки дорівнює
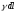 .
Приймемо цю ділянку
.
Приймемо цю ділянку приблизно
за точку,
віддалену від осі
приблизно
за точку,
віддалену від осі
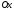 на відстань
на відстань .
Тоді диференціал статичного моменту
.
Тоді диференціал статичного моменту
 («елементарний момент») буде дорівнювати
(«елементарний момент») буде дорівнювати
 ,
тобто
,
тобто
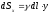 (див. рис. 196).
(див. рис. 196).
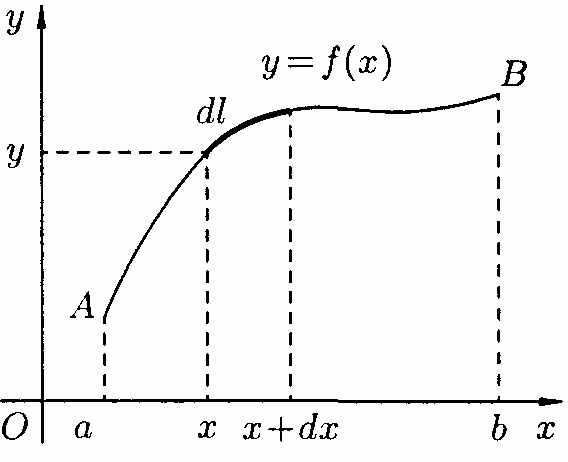
(рис.196)
Звідси
випливає, що статичний момент
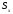 кривої
кривої
 відносно осі
відносно осі
 дорівнює
дорівнює
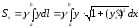 .
.
Аналогічно
знаходимо
 :
:
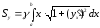 .
.
Статичні
моменти
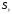 і
і
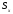 кривої
дозволяють легко встановити положення
її центру ваги (центру мас).
кривої
дозволяють легко встановити положення
її центру ваги (центру мас).
Центром
маси
матеріальної
плоскої кривої
 називається точка площини, що володіє
наступною властивістю: якщо в цій точці
зосередити всю масу
називається точка площини, що володіє
наступною властивістю: якщо в цій точці
зосередити всю масу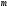 заданої кривої, то статичний момент
цієї точки відносно будь-якої координатної
осі буде рівний статичному моменту
всієї кривої
заданої кривої, то статичний момент
цієї точки відносно будь-якої координатної
осі буде рівний статичному моменту
всієї кривої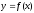 відносно цієї ж осі. Позначимо через
відносно цієї ж осі. Позначимо через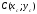 центр мас кривої
центр мас кривої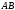 .
.
З
означення центру мас отримаємо рівність
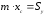 і
і
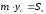 або
або
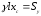 і
і
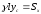 .
Звідси
.
Звідси
 або
або
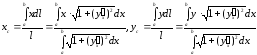 .
.
Приклад
9.7.14.
Знайти
центр мас однорідної дуги кола
 ,
розташованої в першій координатній
четверті (див. рис. 197).
,
розташованої в першій координатній
четверті (див. рис. 197).
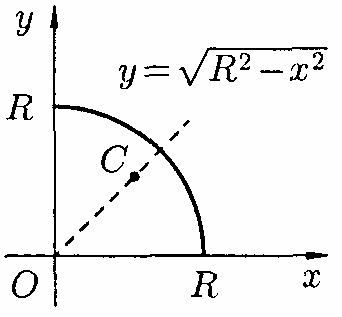
(рис.197)
○ Очевидно, довжина вказаної дуги
кола
рівна
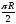 ,
тобто
,
тобто
 .
Знайдемо статичний момент її відносно
осі
.
Знайдемо статичний момент її відносно
осі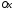 .
Оскільки рівняння дуги є
.
Оскільки рівняння дуги є
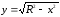 і
і
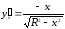 ,
то
,
то
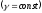

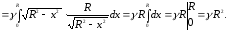
Отже,
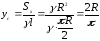
Оскільки дана дуга симетрична відносно бісектриси першого координатного кута, то
 .
Отже, центр мас має координати
.
Отже, центр мас має координати
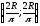 .
●
.
●
Обчислення статичних моментів і координат центру мас плоскої фігури
Нехай
дана плоска матеріальна фігура
(пластинка), обмежена кривою
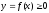 і прямими
і прямими
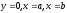 (див. рис. 198).
(див. рис. 198).

(рис.198)
Вважатимемо,
що поверхнева густина пластинки постійна
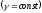 .
Тоді маса всієї пластинки рівна
.
Тоді маса всієї пластинки рівна
 ,
тобто
,
тобто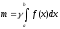 .
Виділимо елементарну ділянку пластинки
в виді нескінченної вузької вертикальної
смуги, приблизно вважатимемо її
прямокутником.
.
Виділимо елементарну ділянку пластинки
в виді нескінченної вузької вертикальної
смуги, приблизно вважатимемо її
прямокутником.
Тоді
маса його рівна
 .
Центр мас
.
Центр мас
 прямокутника лежить на перетині
прямокутника лежить на перетині
діагоналей
прямокутника. Ця точка
 віддалена від осі
віддалена від осі
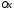 на
на
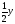 ,
а від осі
,
а від осі
 на
на
 (приблизно: точніше на відстань
(приблизно: точніше на відстань
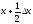 ).
Тоді для елементарних статичних моментів
відносно осей
).
Тоді для елементарних статичних моментів
відносно осей
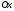 і
і
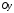 виконані співвідношення.
виконані співвідношення.
 і
і
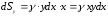
Отже,
 ,
,
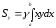
По
аналогії з плоскою кривою отримаємо,
позначивши координати центру мас плоскої
фігури (пластинки) через
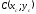 ,
що
,
що
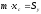 ,
,
 .
Звідси
.
Звідси
 і
і
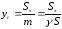
або
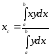 ,
,
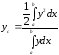
Приклад
9.7.15.
Знайдемо координати центру мас півкола
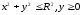
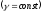 (див.
рис. 199).
(див.
рис. 199).
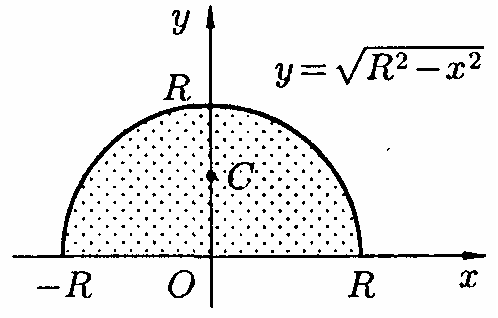
(рис.199)
○ Очевидно
(зважаючи на симетрію фігури відносності
осі
 ),
що
),
що
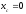 .
Площа півкола дорівнює
.
Площа півкола дорівнює
 .
Знайдемо
.
Знайдемо
 :
:
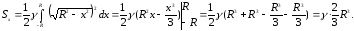
Отже,
 .
.
Отже,
центр мас має координати
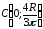 .
●
.
●
