
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
9.7.3. Обчислення довжини дуги плоскої кривої.
Нехай
в прямокутних координатах дана плоска
крива
![]() ,
рівняння якої
,
рівняння якої
![]() ,
де
,
де
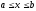 .
.
Під довжиною дуги розуміється границя, до якої прямує довжина ламаної лінії, вписаної в цю дугу, коли число ланок необмежено зростає, а довжина найбільшої ланки прямує до нуля.
Покажемо,
що якщо функція
![]() її похідна
її похідна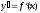 неперервна на відрізку
неперервна на відрізку![]() ,
то крива
,
то крива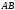 ,
має довжину, рівну
,
має довжину, рівну
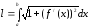 .
(9.7.3)
.
(9.7.3)
Застосуємо першу схему (метод сум).

(рис.183)
Точками
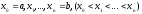 розіб'ємо відрізок
розіб'ємо відрізок
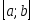 на
на

частин
(див. рис. 183). Нехай цим точкам відповідають
точки
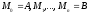 на кривій
на кривій
![]() .
Проведемо хорди
.
Проведемо хорди
 ,
довжини яких позначимо відповідно через
,
довжини яких позначимо відповідно через
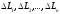 .
Отримаємо ламану
.
Отримаємо ламану
 ,
довжина якої рівна
,
довжина якої рівна
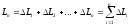 .
.
Довжину хорди (або ланки ламаної)
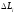 можна знайти за теоремою Піфагора
можна знайти за теоремою Піфагора
з
трикутника з катетами
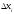 і
і
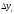 :
:
 ,
де
,
де
 .
.
По
теоремі Лагранжа про скінчений приріст
функції
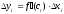 ,
де
,
де
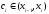 .
Тому
.
Тому
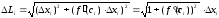 ,
а довжина всіх ламаних
,
а довжина всіх ламаних
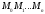 рівна
рівна
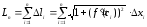 .
(9.7.4)
.
(9.7.4)
Довжина
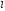 кривою
кривою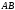 ,
по означенню, дорівнює
,
по означенню, дорівнює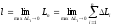 .
.
Помітимо,
що при
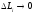 також і
також і
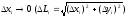 і, отже,
і, отже,
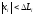 .
Функція
.
Функція
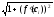 неперервна на відрізку
неперервна на відрізку![]() ,
оскільки, по умові, неперервна функція
,
оскільки, по умові, неперервна функція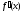 .
Отже, існує границя інтегральної суми
(9.7.4), коли
.
Отже, існує границя інтегральної суми
(9.7.4), коли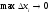 :
:
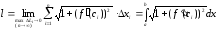 .
.
Таким
чином
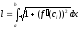 ,
або в скороченому записі
,
або в скороченому записі
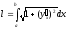 .
.
Якщо рівняння кривої задано в параметричній формі
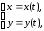
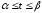 ,
,
де
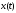 і
і
 —неперервні
функції з неперервними похідними і
—неперервні
функції з неперервними похідними і
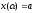 і
і
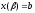 ,
то довжина
,
то довжина
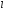 кривою
кривою
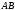 знаходиться по формулі
знаходиться по формулі
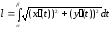 .
(9.7.5)
.
(9.7.5)
Формула
(9.7.4) може бути отримана з формули (9.7.1)
підстановкою
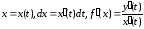 .
.
Приклад
9.7.4.
Знайти
довжину кола радіусу
 .
.
○
Знайти
 частину
її довжини від точки
частину
її довжини від точки
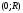 до точки
до точки
 (див.рис.
184).
(див.рис.
184).
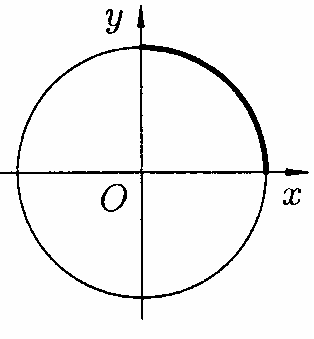
(рис.184)
Оскільки
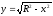 ,
то
,
то
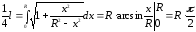 .
.
Значить,
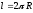 .
Якщо рівняння кола записати в параметричному
вигляді
.
Якщо рівняння кола записати в параметричному
вигляді
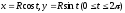 ,
то
,
то
 .●
.●
Обчислення довжини дуги може бути засновано застосуванням методу диференціала. Покажемо, як можна отримати формулу (9.7.3), застосувавши другу схему (метод диференціала).
Візьмемо довільне значення
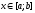 і розглянемо змінний
і розглянемо змінний
відрізок
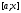 .
На ньому величина
.
На ньому величина
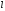 стає функцією від
стає функцією від
 ,
тобто
,
тобто
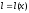
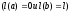 .
.
Знаходимо диференціал
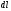 функції
функції
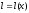 при зміні
при зміні
 на малу величину
на малу величину
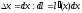 .
Знайдемо
.
Знайдемо
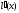 ,
замінюючи нескінченно малу дугу
,
замінюючи нескінченно малу дугу
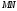 хордою
хордою
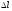 ,
що стягує цю дугу (див. рис. 185):
,
що стягує цю дугу (див. рис. 185):
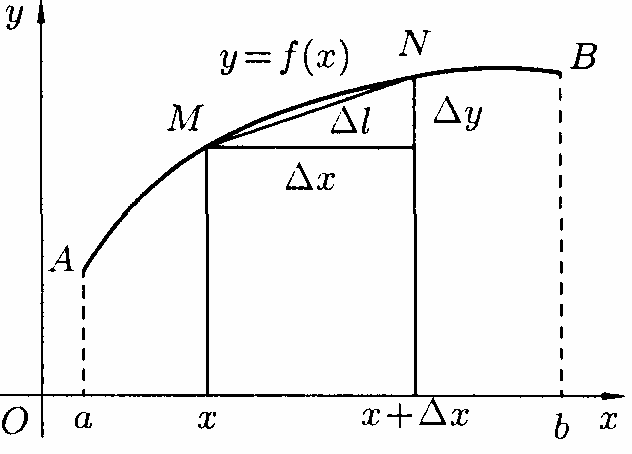
(рис.185)
 .
.
Отже,
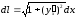 .
.
Інтегруючи
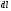 в межах від
в межах від
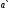 до
до
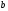 ,
отримаємо
,
отримаємо
 .
.
Рівність
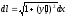 називається формулою диференціала
дуги
в
називається формулою диференціала
дуги
в
прямокутних координатах.
Оскільки
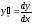 ,
то
,
то
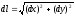 .
.
Остання
формула є теоремою Піфагора для
нескінченно рисого
трикутника
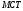 (див. рис. 186).
(див. рис. 186).
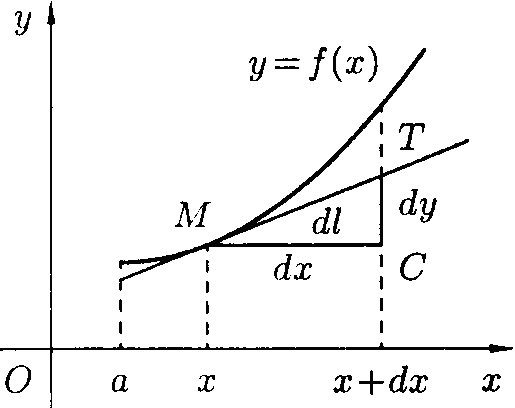
(рис.186)
Нехай
крива
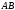 задана рівнянням в полярних координатах
задана рівнянням в полярних координатах
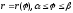 .
Припустимо, що
.
Припустимо, що
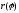 і
і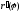 неперервні на відрізку
неперервні на відрізку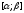 .
.
Якщо
в рівностях
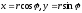 ,
що зв'язують полярні і декартові
,
що зв'язують полярні і декартові
координати,
параметром вважати кут
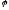 ,
то криву
,
то криву
 можна задати параметрично
можна задати параметрично
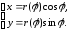 .
.
Тоді
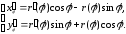 .
.
Тому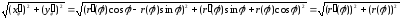
Застосовуючи
формулу (9.7.5), отримаємо
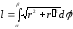 .
.
Приклад
9.7.5.
Знайти
довжину кардіоїди
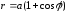 .
.
○
Кардіоїда
 має вигляд, зображений на рис. 187. Вона
симетрична відносно полярної осі.
Знайдемо половину довжини кардіоїди:
має вигляд, зображений на рис. 187. Вона
симетрична відносно полярної осі.
Знайдемо половину довжини кардіоїди:
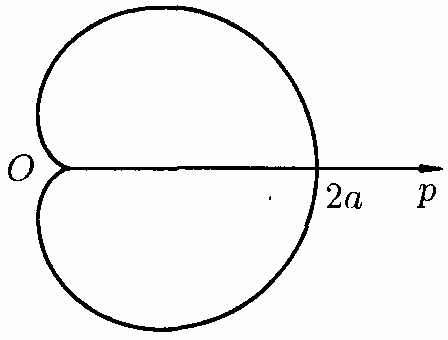
(рис.187)
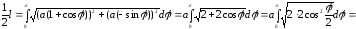
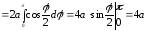 .
.
Таким
чином
 .
Значить,
.
Значить,
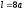 .●
.●
