
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
Нехай
потрібно знайти об'єм
 тіла, причому відомі площі
тіла, причому відомі площі перетинів цього тіла площинами,
перпендикулярними деякій осі, наприклад
осі
перетинів цього тіла площинами,
перпендикулярними деякій осі, наприклад
осі .
.
Застосуємо другу схему (метод диференціала).
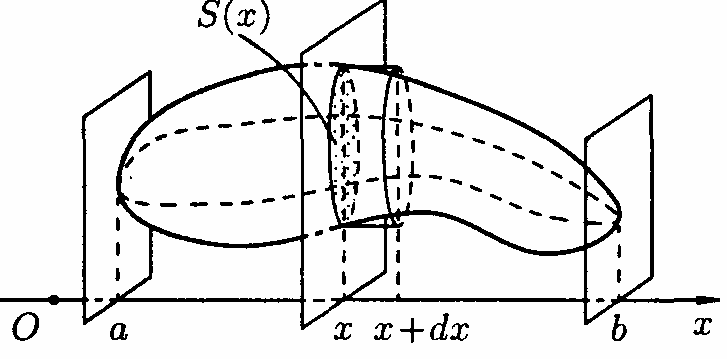
(рис.188)
Через довільну точку
 проведемо площину П, перпендикулярно
осі
проведемо площину П, перпендикулярно
осі (див. рис. 188). Позначимо через
(див. рис. 188). Позначимо через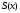 площу
перетину тіла цією площиною;
площу
перетину тіла цією площиною; вважаємо відомою і такою, що неперервно
змінюється при зміні
вважаємо відомою і такою, що неперервно
змінюється при зміні .
Через
.
Через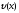 позначимо об'єм частини тіла, лежить
лівіше від площини П будемо вважати,
що на відрізку
позначимо об'єм частини тіла, лежить
лівіше від площини П будемо вважати,
що на відрізку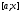 величина
величина є функцією від
є функцією від ,
тобто
,
тобто ((
(( ).
).Знаходимо диференціал
 функції
функції
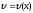 .
Він являє собою «елементарний шар»
тіла, ув'язнений між паралельними
площинами, що перетинають вісь
.
Він являє собою «елементарний шар»
тіла, ув'язнений між паралельними
площинами, що перетинають вісь
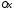 в точках
в точках
 і
і
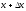 ,
який приблизно може бути прийнятий за
циліндр з основою
,
який приблизно може бути прийнятий за
циліндр з основою
 і висотою
і висотою
 .
Тому диференціал об'єму
.
Тому диференціал об'єму
 .
.Знаходимо шукану величину
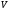 шляхом інтегрування
шляхом інтегрування
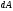 в межах від
в межах від
 до
до
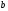 :
:
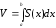 (9.7.6)
(9.7.6)
Отримана формула називається формулою об'єму тіла за площею паралельних перетинів.
Приклад
9.7.6
Знайти
об'єм еліпсоїда
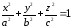 .
.
○
Перетинаючи
еліпсоїд площиною, паралельною площині
 і на відстані
і на відстані від неї
від неї ,
отримаємо еліпс (див. рис. 189):
,
отримаємо еліпс (див. рис. 189):
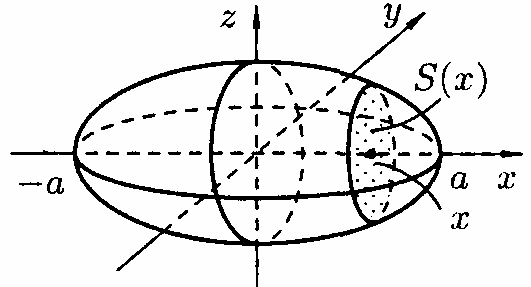
(рис.189)
 .
.
Площа
цього еліпса дорівнює
 .
Тому, по формулі (9.7.6), маємо
.
Тому, по формулі (9.7.6), маємо
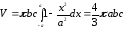 .●
.●
Об'єм тіла обертання
Нехай
навколо осі
 обертається криволінійна трапеція,
обмежена неперервною лінією
обертається криволінійна трапеція,
обмежена неперервною лінією ,
відрізком
,
відрізком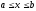 і прямими
і прямими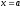 і
і (див. рис. 190). Отримана фігура обертання
називаєтьсятілом
обертання.
Перетин цього тіла площиною, перпендикулярною
осі
(див. рис. 190). Отримана фігура обертання
називаєтьсятілом
обертання.
Перетин цього тіла площиною, перпендикулярною
осі
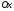 ,
проведеною через довільну точку
,
проведеною через довільну точку осі
осі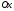 ((
(( ),
є круг з радіусом
),
є круг з радіусом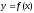 .
Отже,
.
Отже,
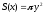 .
.

(рис.190)
Застосовуючи формулу (41.6) об'єму тіла за площею паралельних перетинів, отримаємо
 .
(9.7.7)
.
(9.7.7)
Якщо
криволінійна трапеція обмежена графіком
неперервної функції
 і прямими
і прямими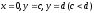 ,
то об'єм тіла, утвореного обертанням
цієї трапеції навколо осі
,
то об'єм тіла, утвореного обертанням
цієї трапеції навколо осі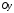 ,
по аналогії з формулою (9.7.7), дорівнює
,
по аналогії з формулою (9.7.7), дорівнює
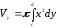 .
(9.7.8)
.
(9.7.8)
Приклад
9.7.7.
Знайти
об'єм тіла, утвореного обертанням фігури,
обмеженої лініями
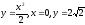 навколо осі
навколо осі (див. рис.191).
(див. рис.191).

(рис.191)
○ По формулі (9.7.8) знаходимо:
 .
●
.
●
9.7.5. Обчислення площі поверхні обертання.
Нехай
крива
 є графіком функції
є графіком функції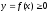 ,
де
,
де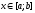 ,
а функція
,
а функція і її похідна
і її похідна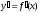 неперервні на цьому відрізку.
неперервні на цьому відрізку.
Знайдемо
площу
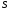 поверхні, утвореної обертанням кривої
поверхні, утвореної обертанням кривої
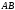 навколо осі
навколо осі
 .
.
Застосуємо другу схему (метод диференціала).
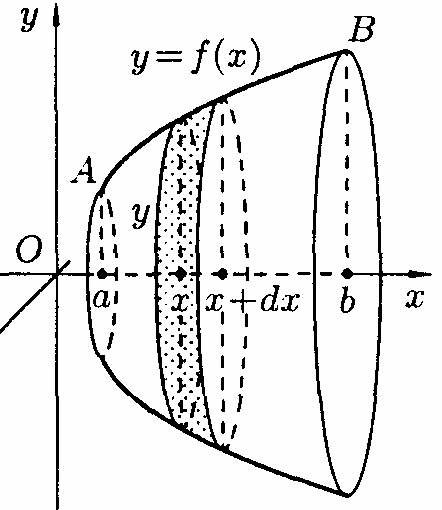
(рис.192)
Через довільну точку
 проведемо площинуП,
перпендикулярну осі
проведемо площинуП,
перпендикулярну осі
 .
Площина П перетинає поверхню обертання
по колу з радіусом
.
Площина П перетинає поверхню обертання
по колу з радіусом
 (див. рис. 192).
(див. рис. 192).
Величина
 поверхні частини фігури обертання, що
лежить лівіше площини, є функцією від
поверхні частини фігури обертання, що
лежить лівіше площини, є функцією від
 ,
тобто
,
тобто
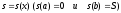 .
.
Дамо аргументу
 приріст
приріст
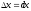 .
Через точку
.
Через точку
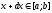 також
також
проведемо
площину, перпендикулярну осі
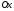 .
Функція
.
Функція
 отримає приріст
отримає приріст ,
зображений на рис. виді «поясочка».
,
зображений на рис. виді «поясочка».
Знайдемо
диференціал площі
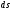 ,
замінюючи утворену між перетинами
фігуру усіченим конусом, твірна якого
рівна
,
замінюючи утворену між перетинами
фігуру усіченим конусом, твірна якого
рівна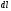 ,
а радіуси основ рівні
,
а радіуси основ рівні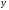 і
і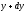 .
Площа його бічної поверхні рівна
.
Площа його бічної поверхні рівна .
Відкидаючи добутки
.
Відкидаючи добутки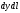 ,
як нескінченно малу вищого порядку, ніж
,
як нескінченно малу вищого порядку, ніж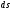 ,
отримаємо
,
отримаємо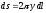 ,
або, оскільки
,
або, оскільки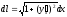 ,
то
,
то .
.
Інтегруючи отриману рівність в межах від
 до
до
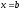 ,
отримаємо
,
отримаємо
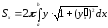 .
(9.7.9)
.
(9.7.9)
Якщо
крива
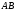 задана параметричними рівняннями
задана параметричними рівняннями
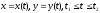 ,
то формула (9.7.9) для площі поверхні
обертання прийме вигляд
,
то формула (9.7.9) для площі поверхні
обертання прийме вигляд
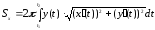 .
.
Приклад
9.7.8.
Знайти
площа поверхні кулі радіусу
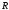 .
.
○
Можна
вважати, що поверхня кулі утворена
обертанням півкола
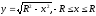 ,
навколо осі
,
навколо осі
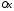 .
По формулі (9.7.9) знаходимо
.
По формулі (9.7.9) знаходимо
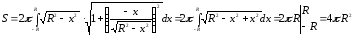 .
●
.
●
