6.2 Непрерывные случайные величины: законы распределения и числовые характеристики.

Случайная величина называется(абсолютно) непрерывной случайной величиной (НСВ), если её функция распределения представляется в виде ,, где-неотрицательная и интегрируемая в бесконечных пределах функция, называемаяфункцией плотности (распределения) вероятностей. Множество возможных значений непрерывной случайной величины несчётно и обычно представляет собой некоторый конечный или бесконечный промежуток числовой прямой.

Функция распределения непрерывной случайной величиныявляется непрерывной неубывающей функцией на всей числовой прямой, причём вероятность попадания в любую фиксированную точку равна нулю:,.

Функция является плотностью вероятностей некоторой НСВ, тогда и только тогда, когда:1); 2).

Если функция распределения случайной величины на числовой прямой всюду непрерывна и почти всюду дифференцируема, то она является функцией распределения непрерывной случайной величины, плотность вероятностей которой в точках, гдедифференцируема, определяется равенством:

.

В точках, где недифференцируема, плотность вероятностей, определяется произвольным образом, чаще всего по непрерывности слева или справа.

Для непрерывной случайной величины с плотностью вероятностей

.

Математическим ожиданием непрерывной случайной величины называется число, если интеграл сходится абсолютно.

Дисперсию непрерывной случайной величины вычисляют по формулам:

или .

Модой непрерывной случайной величины называется число, определяемое как точка локального максимума плотности вероятностей. Мода может не существовать, иметь единственное значение (унимодальное распределение) или множество значений (мультимодальное распределение).

Медианой непрерывной случайной величины называется число, удовлетворяющее условиюили.

Начальным моментом -го порядка () распределения случайной величины(если он существует) называется число.

Центральным моментом -го порядка () распределения случайной величины(если он существует) называется число.

Для непрерывной случайной величины начальные и центральные моменты вычисляют по формулам:,.

В задачах 12.146-12.151 непрерывная случайная величиназадана функцией распределения. Требуется:а)найти функцию плотности вероятностей;б)вычислить математическое ожиданиеи дисперсию;в)найти вероятность попадания случайной величины.в интервал.

12.146 ,.

12.147 ,.

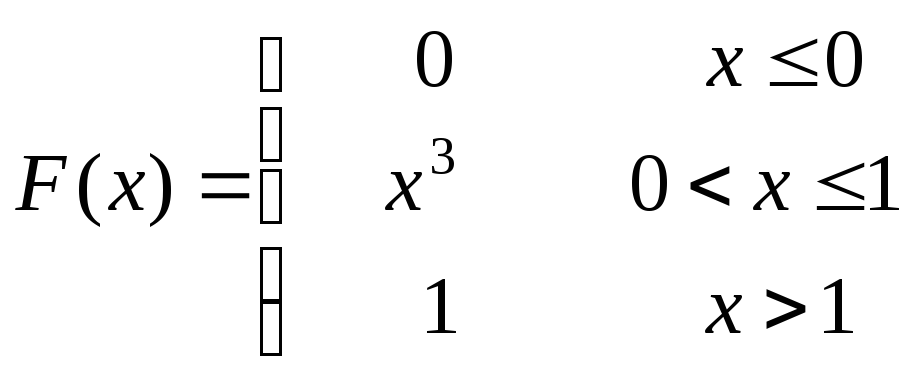
12.148 ,.

12.149 ,.

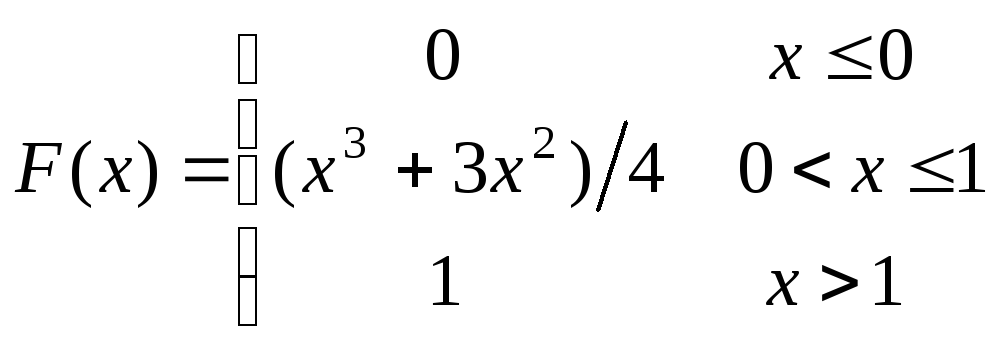
12.150 ,.

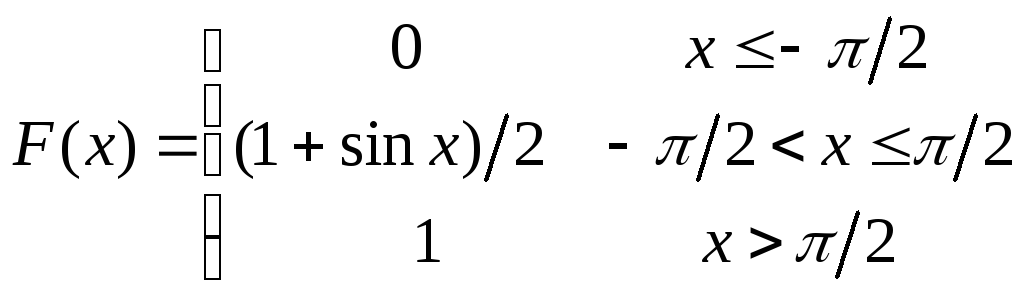
12.151 ,.

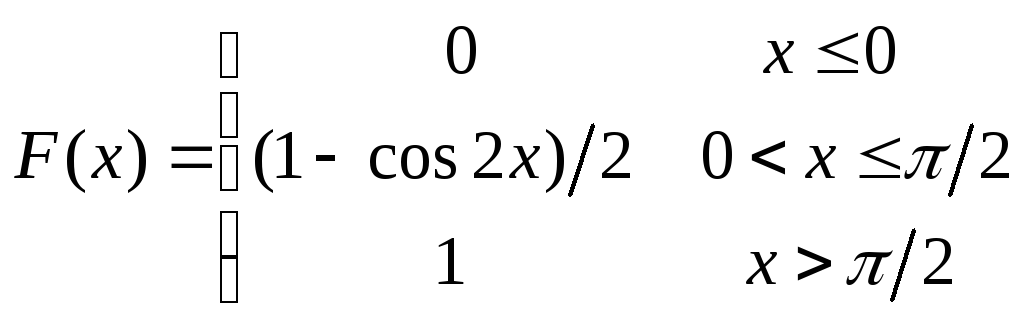
В задачах 12.152-12.155 непрерывная случайная величиназадана функцией плотности вероятностей. Требуется:а)найти функцию распределения;б)вычислить математическое ожиданиеи дисперсию;в)найти вероятность попадания случайной величины.в интервал.

12.152 ,.

12.153 ,.

12.154 ,.

12.155 ,.

В задачах 12.156-12.157 необходимо найти неизвестные константыв выражении для функции распределенияНСВи её математическое ожидание.

12.15612.157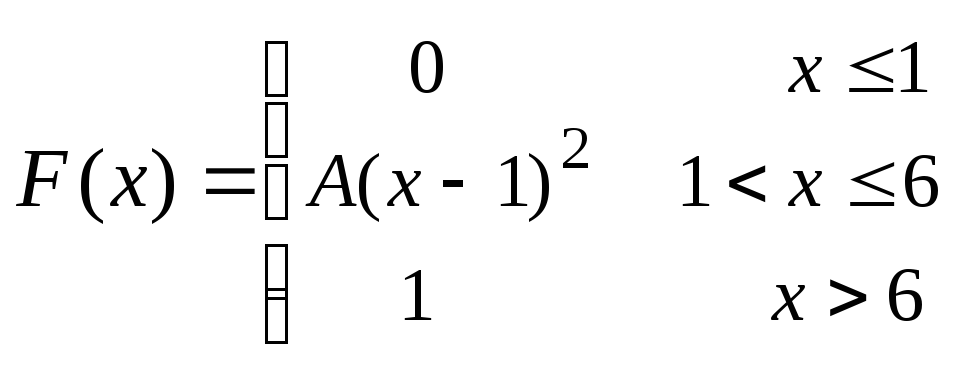

В задачах 12.158-12.159 необходимо найти неизвестные константыв выражении для функции распределенияНСВи вероятностьуказанного интервала.

12.158 ,,.

12.159 ,.

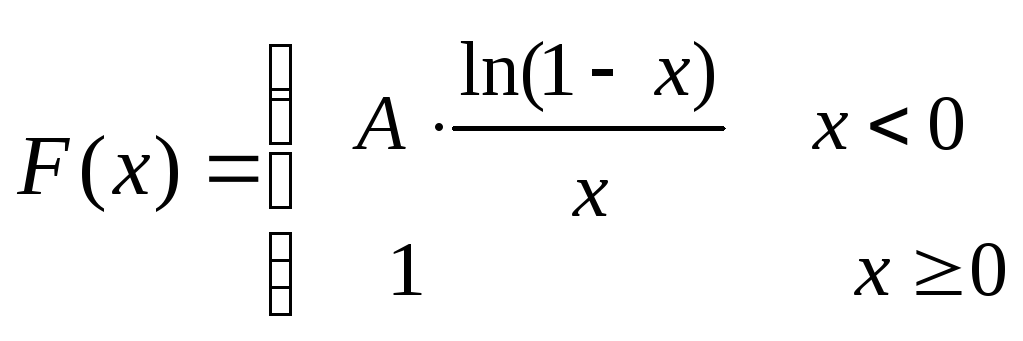
В задачах 12.160-12.164 необходимо найти неизвестную константув выражении для функции плотности вероятностейНСВи вероятностьуказанного интервала.

12.160 ,.

12.161 ,.

12.162 ,.

12.163 ,.

12.164 ,.

12.165 Случайная величиназадана функцией распределения. Найти вероятность того, что в результате четырёх независимых испытаний величинатри раза примет значение, принадлежащее интервалу, если .

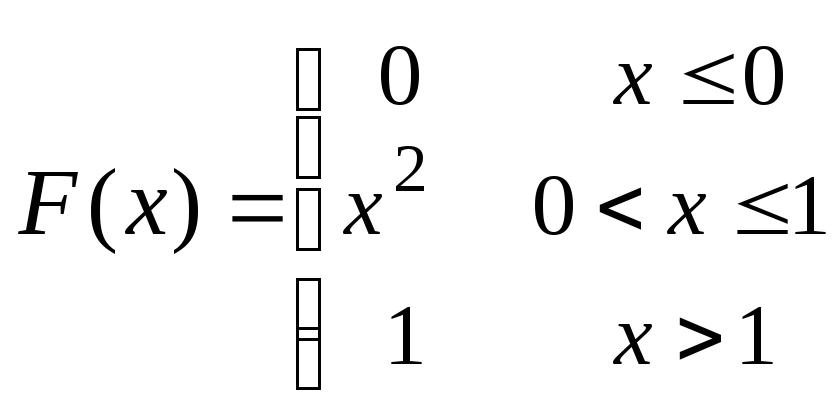12.166 Случайная величиназадана функцией плотности вероятностей .Найти вероятность того, что в трёх независимых испытаниях величинадва раза примет значение, принадлежащее интервалу.

12.167 Случайная величиназадана функцией плотности вероятностей. Найти модувеличины, если:

а)

б)

12.168 Случайная величиназадана функцией плотности вероятностей. Найти медианувеличины, если:

а)б)

12.169 Доказать, что центральные моменты второго, третьего и четвёртого порядков:случайной величинысвязаны с её начальными моментами первого, второго, третьего и четвёртого порядков:равенствами:а);

б) ; в).

12.170 Случайная величиназадана функцией плотности вероятностей. Требуется вычислить её начальные и центральные моменты:,; коэффициенты асимметриии эксцесса, если:

а) б)