§ 4. Проекция силы на ось и плоскость.

Аналитический способ сложения сил

Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси ( рис. 11).

F_x = Fcos , Q_x = Qcos₁ = – Qcos , P_x = 0. (4)

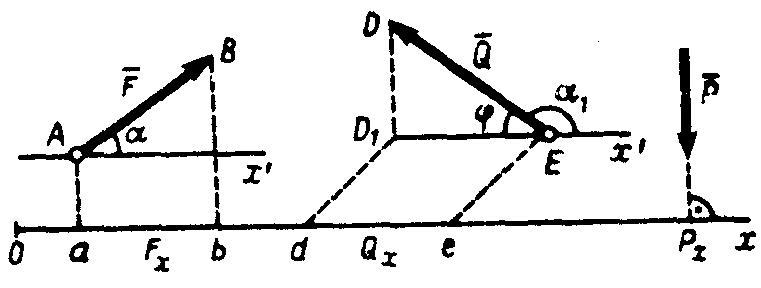
Рис. 11

Проекцией силы на плоскость Oxy называется вектор, заключенный между проекциями начала и конца силы на эту плоскость (рис. 12).

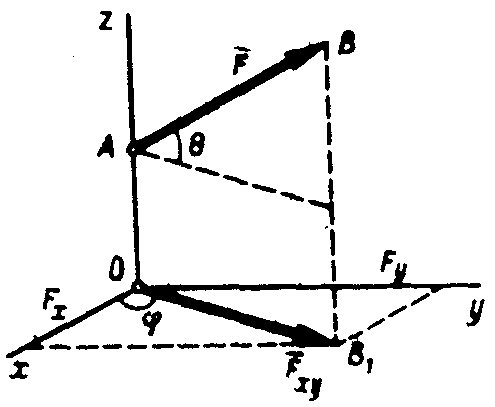
Рис. 12

В некоторых случаях для нахождения проекции силы на ось удобнее найти сначала ее проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроектировать на данную ось (рис. 12):

F_x = F_xycos = Fcoscos , F_y = F_xysin = Fcossin . (5)

Силу можно построить, если известны модуль F этой силы, углы, , , которые сила образует с координатными осями и координаты x, y, z точки приложения.

Для решения задач механики удобнее задавать силу ее проекциями F_x = X , F_y = Y , F_z = Z на координатные оси. Зная проекции, можно определить модуль силы и углы, которые она образует с координатными осями по формулам

,

cos = X / F , cos = Y / F , cos = Z / F . (6)

Если есть главный вектор системы сил ,,, …,, т.е., то проекциями вектора на оси координат будут:

, ,

Зная R_x, R_y, R_z, по формулам (6) находим модуль главного вектора и его направляющие косинусы:

,

cos = R_x / R , cos = R_y / R , cos = R_z / R . (7)

Формулы (7) позволяют решить задачу о сложении сил аналитически.

Для сил, расположенных в одной плоскости, соответствующие формулы принимают вид:

, ,

, cos = R_x / R , cos = R_y / R . (8)

Если силы заданы их модулями и углами с осями, то для применения аналитического метода сложения надо предварительно вычислить проекции этих сил на координатные оси.

Задача 1. Найти сумму трех лежащих в одной плоскости сил (рис. 13, а ), если дано: F = 17,32 Н, T = 10 Н, P = 24 ,  = 30⁰,  = 60⁰.

Решение

Вычисляем проекции заданных сил на координатные оси:

F_x = Fcos = 17,32·0,866 = 15 Н, T_x = – Tcos = – 10·0,5 = – 5 Н, P_x = 0,

F_y = – Fsin = 17,32·0,5 = – 8,66 Н, T_y = – Tsin = 10·0,866 = 8,66 Н,

P_y = – P = –24 Н.

Тогда по формулам (8)

R_x = 15 – 5 = 10 Н , R_y = – 8,66 + 8,66 – 24 = – 24 Н .

Следовательно

Н ; cos = 5 / 13 , cos = – 12 / 13 .

Окончательно R = 26 Н,  = 67⁰20^,  = 157⁰20^.

Для решения задачи геометрическим методом выберем соответствующий масштаб (например, в 1см – 10 Н) и построим из сил ,,, силовой многоугольник (рис. 13, б). Его замыкающая ad определяет в данном масштабе модуль и направление. Если, например, при измерении получим ad ≈ 2,5 см, то R ≈ 25 Н с погрешностью по отношению к точному решению около 4 %.

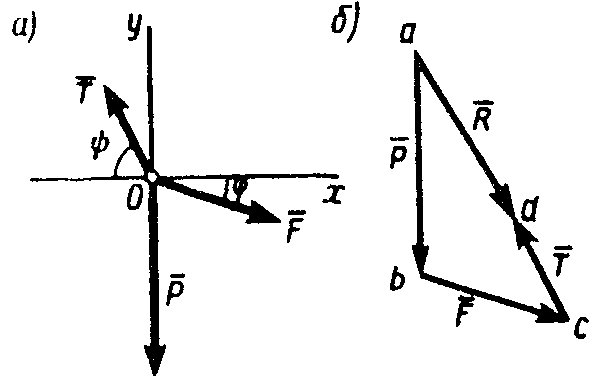
Рис. 13

§5. Равновесие системы сходящихся сил

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая, а следовательно, и главный вектор этих сил были равны нулю. Условия, которым при этом должны удовлетворять силы, можно выразить в геометрической или аналитической форме.

1. Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.

2. Аналитические условия равновесия. Модуль главного вектора системы сил определяется первой формулой (7):

.

Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно R_x = 0, R_y = 0, R_z = 0, т.е. когда действующие на тело силы будут удовлетворять равенствам

, ,. (9)

Равенства (9) выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на координатные оси были равны нулю.

Если сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В этом случае получим только два условия равновесия:

, . (10)

3. Теорема о трех силах. Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия сил пересекаются в одной точке.

Для доказательства теоремы сначала рассмотрим две силы, например и. Линии действия этих сил пересекаются в некоторой точке А (рис. 14). Заменим их равнодействующей. Тогда на тело будут действовать две силы: силаи сила, приложенная в какой-то точке В тела. Так как тело находится в равновесии, то согласно первой аксиоме, силыинаправлены вдоль прямой АВ. Следовательно, линия действия силытоже проходит через точку А, что и требовалось доказать.

Пример. Рассмотрим брус АВ, закрепленный в точке А шарниром и опирающийся на выступ D (рис. 15).На этот брус действуют три силы: сила тяжести , реакциявыступа и реакцияшарнира. Так как брус находится в равновесии, то линии действия сил должны пересекаться в одной точке. Линии действия силиизвестны и они пересекаются в точке К. Следовательно, линия действия реакциитоже должна пройти через точку К, т. е. должна быть направлена вдоль прямой АК.

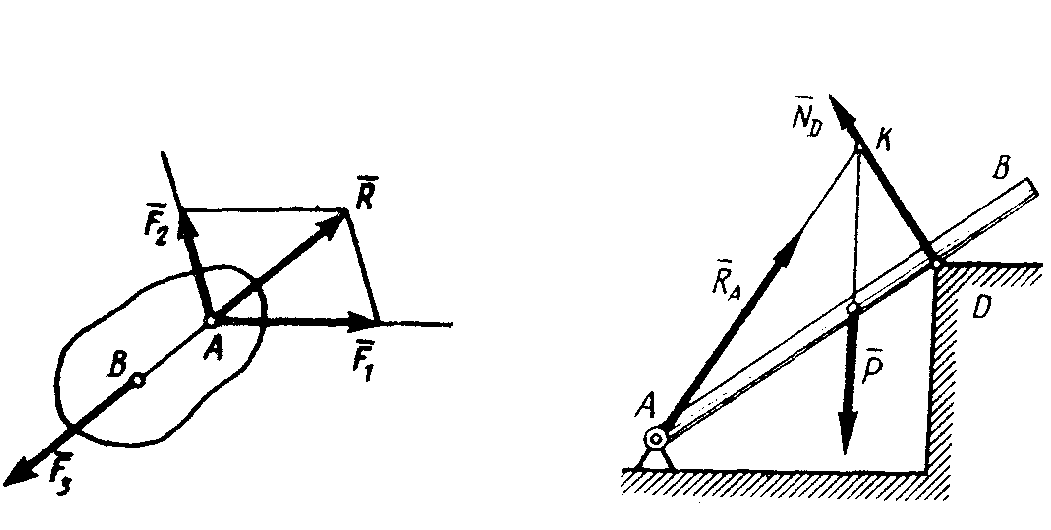
Рис. 14 Рис. 15

Задача 2. Груз весом Р лежит на гладкой наклонной плоскости с углом наклона (рис. 16, а). Определить значение горизонтальной силы , которую надо приложить к грузу, чтобы удержать его в равновесии, и найти, чему при этом равна сила давлениягруза на плоскость.

Решение. Искомые силы действуют на разные тела: сила на груз, сила – на плоскость. Для решения задачи вместо силы будем искать реакцию плоскости., Q = N. Тогда заданная сила и искомые силыибудут действовать на одно и то же тело на груз. Рассмотрим равновесие груза.

Геометрический способ. При равновесии треугольник, построенный из сил ,и, должен быть замкнутым. Построение треугольника начнем с заданной силы. От произвольной точкиa в выбранном масштабе откладываем силу (рис. 16, б). Через начало и конец этой силы проводим прямые, параллельные направлениям сил и. Точка пересечения этих прямых дает третью вершинуc замкнутого силового треугольника abc, в котором стороны bc и ac равны в выбранном масштабе силам и. Направление сил определяется правилом стрелок: так как равнодействующая равна нулю, то при обходе треугольника острия стрелок нигде не должны встречаться в одной точке. Модули искомых сил можно найти из треугольникаabc путем численного расчета (в этом случае соблюдать масштаб при изображении сил не надо). Замечая, что  bac = 90⁰,  abc =  получим F = Ptg , N = P / cos (F / P = tg , P / N = cos).

Рис. 16

Аналитический способ. Так как система сходящихся сил является плоской, то для нее надо составить два условия равновесия (10)

, .

Для этого сначала проводим координатные оси. Затем вычисляем проекции сил ,ина осиx и y и составляем уравнения, получим:

, .

Решая эти уравнения, найдем:

, .