
- •Введение
- •Глава 1. Исходные положения статики.
- •§1. Аксиомы статики
- •§ 2. Связи и их реакции
- •§ 3. Геометрический способ сложения сил.
- •§ 4. Проекция силы на ось и плоскость.
- •§5. Равновесие системы сходящихся сил
- •Глава 2 момент силы относительно центра. Пара сил
- •§6. Момент силы относительно центра (или точки)
- •§7. Алгебраический момент силы относительно центра
- •§8. Пара сил. Момент пары
- •§ 9. Алгебраический момент пары сил
- •Глава 3. Приведение системы сил к центру. Условия равновесия
- •§10. Теорема о параллельном переносе силы
- •§11. Приведение произвольной системы сил к центру
- •§12. Условия равновесия системы сил.
- •§13. Приведение плоской системы сил к простейшему виду
- •§ 14. Равновесие плоской системы сил. Случай параллельных сил
- •§15. Решение задач
- •§16. Равновесие при наличии трения скольжения
- •Глава 4
- •§17. Центр параллельных сил
- •§ 18. Силовое поле. Центр тяжести твердого тела
- •§19. Координаты центров тяжести однородных тел
- •§20. Способы определения координат центров тяжести тел
- •§21. Центры тяжести некоторых однородных тел
§12. Условия равновесия системы сил.
Теорема Вариньона о моменте равнодействующей
Покажем, что для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т. е. чтобы выполнялись условия
![]() ,
,
![]() ,
(24)
,
(24)
где
О – любой центр, так как при
![]() значение
значение![]() от выбора центра О не зависит.
от выбора центра О не зависит.
Условия
(24) являются необходимыми, так как если
какое-нибудь из них не выполняется, то
система действующих на тело сил приводится
или к равнодействующей (когда ![]() ),
или к паре сил (когда
),
или к паре сил (когда ![]() )
и, следовательно, не является уравновешенной.
Одновременно условия (24) являются и
достаточными, потому что при
)
и, следовательно, не является уравновешенной.
Одновременно условия (24) являются и
достаточными, потому что при
![]() система сил может приводится только к
паре с моментом
система сил может приводится только к
паре с моментом![]() ,
а так как
,
а так как ![]() ,
то имеет место равновесие.
,
то имеет место равновесие.
Теорема Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.
Пусть
система сил
![]() ,
,![]() , …,
, …,![]() приводится к равнодействующей
приводится к равнодействующей![]() ,
линия действия которой проходит через
некоторую точку С (рис. 24). Приложим в
этой точке силу
,
линия действия которой проходит через
некоторую точку С (рис. 24). Приложим в
этой точке силу![]() .
Тогда система сил
.
Тогда система сил![]() ,
,![]() , …,
, …,![]() ,
, ![]() будет находиться в равновесии и для нее
должно выполнятся условие
будет находиться в равновесии и для нее
должно выполнятся условие![]() ,
т. е. для данных сил должно быть
,
т. е. для данных сил должно быть
![]() .
.
Но
так как
![]() и обе силы направлены вдоль одной и той
же прямой, то
и обе силы направлены вдоль одной и той
же прямой, то
![]() .
.
Подставляя
это значение
![]() в предыдущее равенство, найдем из него,
что
в предыдущее равенство, найдем из него,
что
![]() .
(25)
.
(25)
Тем самим теорема доказана.
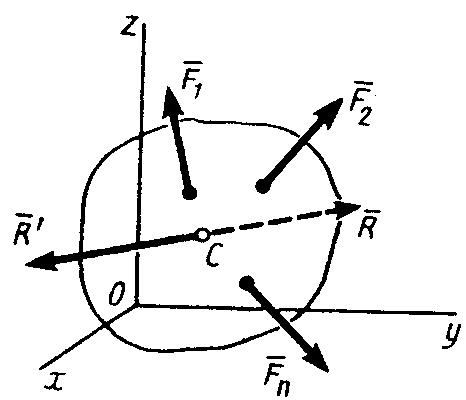
Рис. 24
§13. Приведение плоской системы сил к простейшему виду
Результат,
полученный в §11, справедлив и в частном
случае плоской системы сил. Плоская
система сил тоже приводится к силе,
равной
![]() и приложенной в произвольно выбранном
центре О, и паре сил с моментом
и приложенной в произвольно выбранном
центре О, и паре сил с моментом![]() ,
но сила и пара лежат в данном случае в
одной плоскости – в плоскости действия
сил (рис. 25, а, где пара изображена
дуговой стрелкой). Значения главного
вектора
,
но сила и пара лежат в данном случае в
одной плоскости – в плоскости действия
сил (рис. 25, а, где пара изображена
дуговой стрелкой). Значения главного
вектора
![]() и главного момента
и главного момента![]() даются формулами (22) и (23); при этом вектор
даются формулами (22) и (23); при этом вектор
![]() можно определить или геометрически
построением силового многоугольника
(§ 3), или аналитически по формулам
(8) из § 4.
можно определить или геометрически
построением силового многоугольника
(§ 3), или аналитически по формулам
(8) из § 4.
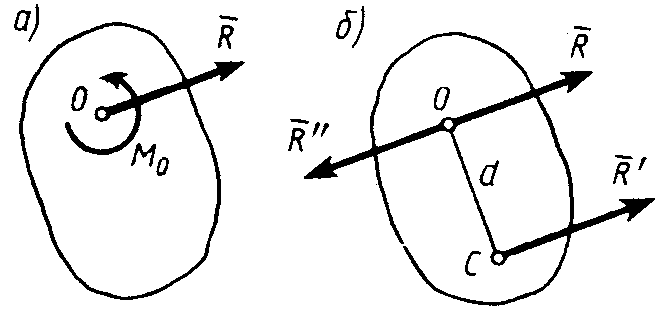
Рис. 25
Таким образом, для плоской системы сил
![]() ,
,
![]() ,
,![]() ,
(26)
,
(26)
где все моменты в равенстве алгебраические и сумма тоже алгебраическая. Найдем, к какому простейшему виду может приводиться данная плоская система сил, не находящаяся в равновесии.
1. Если
для данной системы сил
![]() ,
а
,
а![]() ,
то она приводится к одной паре с моментом
,
то она приводится к одной паре с моментом
![]() .
Как показано в §11, значение
.
Как показано в §11, значение![]() в этом случае не зависит от выбора центра
О.
в этом случае не зависит от выбора центра
О.
2. Если
для данной системы сил ![]() ,
то она приводится к одной силе, т.е. к
равнодействующей. При этом возможны
два случая:
,
то она приводится к одной силе, т.е. к
равнодействующей. При этом возможны
два случая:
а) ![]() ,
,![]() .
В этом случае система приводится к
равнодействующей
.
В этом случае система приводится к
равнодействующей![]() ,
проходящей через центр О;
,
проходящей через центр О;
б) ![]() ,
,
![]() .
В этом случае пару с моментом
.
В этом случае пару с моментом
![]() можно изобразить двумя силами
можно изобразить двумя силами![]() и
и![]() ,
беря
,
беря![]() ,
а
,
а![]() (рис. 25, б). При этом, если d = OC
– плечо пары, то должно быть
(рис. 25, б). При этом, если d = OC
– плечо пары, то должно быть
![]() .
(27)
.
(27)
Отбросив
теперь силы
![]() и
и![]() ,
как уравновешенные, найдем, что вся
система сил заменяется равнодействующей
,
как уравновешенные, найдем, что вся
система сил заменяется равнодействующей![]() ,
проходящей через точку С. Положение
точки С определяется двумя условиями:
1) расстояние OC = d (
,
проходящей через точку С. Положение
точки С определяется двумя условиями:
1) расстояние OC = d (![]() )
должно удовлетворять равенству (27);
2) знак момента относительно центра
О силы
)
должно удовлетворять равенству (27);
2) знак момента относительно центра
О силы![]() ,
приложенной в точке С, т.е. знак
,
приложенной в точке С, т.е. знак![]() ,
должен совпадать со знакомMO.
,
должен совпадать со знакомMO.
Таким
образом, плоская система сил, не
находящаяся в равновесии, может быть
окончательно приведена или к одной
силе, т.е. к равнодействующей (когда ![]() ),
или к паре сил (когда
),
или к паре сил (когда ![]() ).
).
