
- •§2. Свободный вектор
- •§3. Сложение и вычитание свободных векторов
- •§4. Умножение свободного вектора на число
- •Лекция 2. Векторное пространство. Базис и координаты вектора §5. Понятие векторного пространства
- •§6. Линейная зависимость векторов
- •§7. Базис векторного пространства. Координаты вектора
- •Лекция 3. Скалярное умножение свободных векторов §8. Проекция вектора на вектор
- •§9. Скалярное умножение свободных векторов
- •Лекция 4 - 5. Векторное и смешанное умножение свободных векторов §10. Ориентация векторного пространства
- •§11. Векторное умножение свободных векторов
- •§12. Смешанное умножение свободных векторов
- •Раздел II. Аналитическая планиметрия Лекция 1. Аффинные системы координат на плоскости. Метод координат §1. Аффинная система координат на плоскости
- •§2. Формулы преобразования координат
- •§3. Метод координат на плоскости
- •Лекция 2. Прямая на плоскости как линия первого порядка §4. Уравнение прямой на плоскости
- •§5. Особенности расположения прямой относительно системы координат
- •Лекция 3. Аналитическое задание полуплоскостей. Вычисление расстояний и углов на плоскости §6. Геометрический смысл знака трехчлена прямой
- •§7. Расстояние от точки до прямой
- •§8. Взаимное расположение двух прямых на плоскости
- •§9. Угол между прямыми
- •Лекция 4. Конические сечения: эллипс, гипербола, парабола §10. Эллипс
- •§11. Гипербола
- •§12. Парабола
- •§13. Директориальное свойство эллипса и гиперболы
- •Лекция 5. Классификация линий второго порядка на плоскости §14. Приведение общего уравнения линии второго порядка к каноническому виду
- •Лекция 6. Общая теория линий второго порядка §15. Центр линии второго порядка
- •§16. Взаимное расположение линии второго порядка и прямой
- •§19. Диаметры линий второго порядка
- •§20. Главные направления, главные диаметры
- •Литература
Лекция 4. Конические сечения: эллипс, гипербола, парабола §10. Эллипс
О п р е д е л е н и е. Эллипсом называется множество всех точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами:
![]() .
.
Чтобы найти уравнение эллипса, нужно удобным образом выбрать систему координат.
![]() ,
где
,
где
![]() – середина отрезка
– середина отрезка![]() ,
,![]() .
Тогда
.
Тогда![]() .
Под уравнением фигуры понимаем уравнение,
которому удовлетворяют координаты
любой точки, принадлежащей фигуре, и не
удовлетворяют координаты точек, не
принадлежащих фигуре. Поэтому, вывод
уравнения эллипса состоит из двух
этапов: сначала находим уравнение,
которому удовлетворяют координаты
любой точки эллипса, затем показываем,
что если координаты точки удовлетворяют
этому уравнению, то точка принадлежит
эллипсу.
.
Под уравнением фигуры понимаем уравнение,
которому удовлетворяют координаты
любой точки, принадлежащей фигуре, и не
удовлетворяют координаты точек, не
принадлежащих фигуре. Поэтому, вывод
уравнения эллипса состоит из двух
этапов: сначала находим уравнение,
которому удовлетворяют координаты
любой точки эллипса, затем показываем,
что если координаты точки удовлетворяют
этому уравнению, то точка принадлежит
эллипсу.
I.
![]() .
Используя формулы вычисления расстояния
между точками, получим уравнение, которое
приводится к виду
.
Используя формулы вычисления расстояния
между точками, получим уравнение, которое
приводится к виду![]() ,
где обозначено
,
где обозначено![]() .
.
II.
Пусть координаты точки
![]() удовлетворяют уравнению
удовлетворяют уравнению![]() .
Покажем, что точка
.
Покажем, что точка![]() принадлежит эллипсу, то есть
принадлежит эллипсу, то есть![]() .
.
Непосредственным
вычислением получаем
![]() .
.
Из
уравнения, которому удовлетворяют
координаты точки
![]() ,
следует
,
следует![]() .
Кроме того,
.
Кроме того,![]() .
Поэтому, имеем
.
Поэтому, имеем![]() и
и![]() .
.
Аналогично
находим
![]() .
.
Тогда
![]() и значит, точка
и значит, точка![]() принадлежит эллипсу.
принадлежит эллипсу.
Из
I
и II
следует, что
![]() – уравнение эллипса –каноническое
уравнение эллипса и
значит эллипс – линия второго порядка.
– уравнение эллипса –каноническое
уравнение эллипса и
значит эллипс – линия второго порядка.
Исследование формы эллипса
 .
То есть
.
То есть
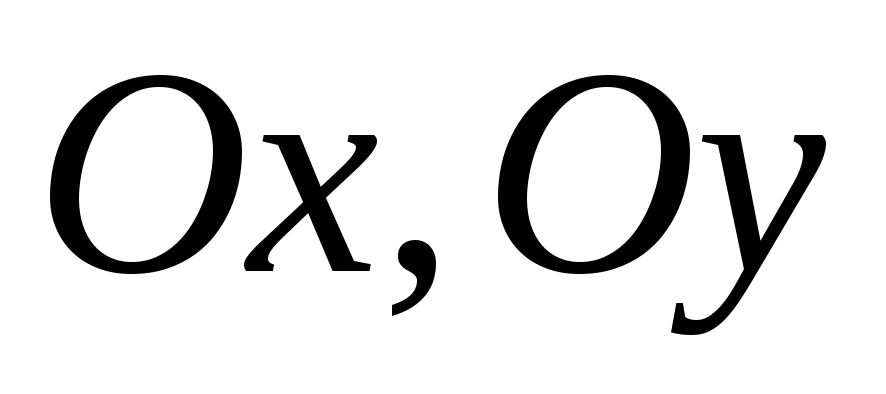 являются осями симметрии, а
являются осями симметрии, а центром симметрии.
центром симметрии. .
Так как
.
Так как
 ,
то все точки эллипса находятся внутри
прямоугольника, определяемого прямыми
,
то все точки эллипса находятся внутри
прямоугольника, определяемого прямыми .
.Определяя точки пересечения эллипса с произвольной прямой
 ,
проходящей через начало системы
координат, получим систему уравнений
,
проходящей через начало системы
координат, получим систему уравнений .
Тогда
.
Тогда .
Таким образом, любая прямая, проходящая
через начало координат, пересекает
эллипс в двух точках, симметричных
относительно
.
Таким образом, любая прямая, проходящая
через начало координат, пересекает
эллипс в двух точках, симметричных
относительно .
В частности
.
В частности
![]() .
.
Точки
![]() называются вершинами эллипса,
называются вершинами эллипса,![]() – большой полуосью,
– большой полуосью,![]() – малой полуосью.
– малой полуосью.
Для точек эллипса, находящихся в первой координатной четверти, имеем
 .
Таким образом, если
.
Таким образом, если возрастает от 0 до
возрастает от 0 до ,
то
,
то убывает от
убывает от до 0.
до 0.Эксцентриситетом эллипса называется число
 .
Таким образом, эксцентриситет эллипса
меньше 1.
.
Таким образом, эксцентриситет эллипса
меньше 1.
Имеем
![]() .
Отсюда
.
Отсюда![]() .
Для системы эллипсов с одной и той же
большой осью (
.
Для системы эллипсов с одной и той же
большой осью (![]() постоянно) видим, что с увеличением
эксцентриситета уменьшается малая ось,
то есть эллипс становится более
сплюснутым. При
постоянно) видим, что с увеличением
эксцентриситета уменьшается малая ось,
то есть эллипс становится более
сплюснутым. При![]() будем иметь
будем иметь![]() и эллипс становится окружностью.
и эллипс становится окружностью.
§11. Гипербола
О
п р е д е л е н и е. Гиперболой называется
множество всех точек плоскости, модуль
разности расстояний от которых до двух
заданных точек, называемых фокусами,
есть величина постоянная, меньшая, чем
расстояние между фокусами:
![]() .
.
По
аналогии с эллипсом можно вывести
каноническое
уравнение гиперболы:
![]() ,
где обозначено
,
где обозначено![]() .
.
Исследование формы гиперболы
 –оси
симметрии,
–оси
симметрии,
 – центр симметрии гиперболы.
– центр симметрии гиперболы. .
Из уравнения гиперболы следует, что
.
Из уравнения гиперболы следует, что
 ,
то есть все точки гиперболы находятся
вне полосы, определяемой прямыми
,
то есть все точки гиперболы находятся
вне полосы, определяемой прямыми .
.Поиск точек пересечения гиперболы с
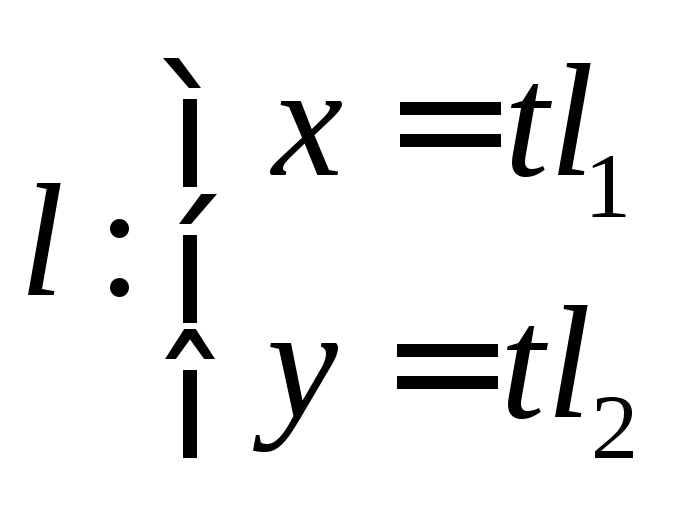 – произвольной прямой, проходящей
через начало системы координат, сводится
к решению уравнения
– произвольной прямой, проходящей
через начало системы координат, сводится
к решению уравнения .
Таким образом, если
.
Таким образом, если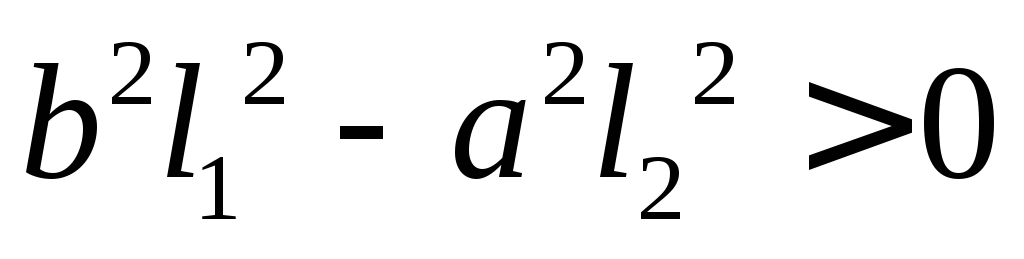 ,
то прямая
,
то прямая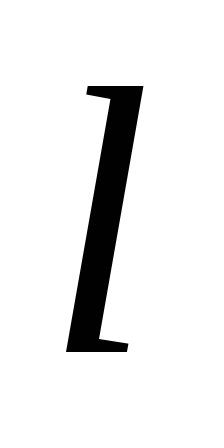 пересекает гиперболу в двух точках,
симметричных относительно начала
системы координат.
пересекает гиперболу в двух точках,
симметричных относительно начала
системы координат.
Если
![]() ,
то прямая
,
то прямая![]() не пересекает гиперболу.
не пересекает гиперболу.
При
этом
 и,
следовательно,
и,
следовательно, .
.
Получаем,
что прямая
![]() не пересекает гиперболу, если её угловой
коэффициент по модулю больше, чем модуль
углового коэффициента прямой
не пересекает гиперболу, если её угловой
коэффициент по модулю больше, чем модуль
углового коэффициента прямой![]() или
или![]() .
Прямые
.
Прямые![]() и
и![]() называютсяасимптотами
гиперболы.
называютсяасимптотами
гиперболы.
Ось
![]() пересекает гиперболу в точках
пересекает гиперболу в точках![]() и
и![]() –вершины
гиперболы.
Ось
–вершины
гиперболы.
Ось
![]() называетсявещественной
осью.
называетсявещественной
осью.
Ось
![]() не имеет с гиперболой общих вещественных
точек и называетсямнимой
осью гиперболы.
не имеет с гиперболой общих вещественных
точек и называетсямнимой
осью гиперболы.
Прямая
 ,
, ,
пересекает гипеболу в точке
,
пересекает гипеболу в точке ,
а асимптоту
,
а асимптоту в точке
в точке .
Расстояние от точки
.
Расстояние от точки до гиперболы меньше, чем расстояние
до гиперболы меньше, чем расстояние .
Видим, что при
.
Видим, что при расстояние
от точки
расстояние
от точки до гиперболы стремится к нулю. То есть
по мере удаления от мнимой оси точки
гиперболы неограниченно приближаются
к соответствующей асимптоте.
до гиперболы стремится к нулю. То есть
по мере удаления от мнимой оси точки
гиперболы неограниченно приближаются
к соответствующей асимптоте.Эксцентриситетом гиперболы называется число
 .
Таким образом, эксцентриситет гиперболы
больше 1.
.
Таким образом, эксцентриситет гиперболы
больше 1.
Имеем
![]() Таким образом, для системы гипербол с
общими вещественными вершинами (
Таким образом, для системы гипербол с
общими вещественными вершинами (![]() постоянно) с возрастанием эксцентриситета
ветви гипербол все более удаляются от
вещественной оси.
постоянно) с возрастанием эксцентриситета
ветви гипербол все более удаляются от
вещественной оси.
