Министерство образования и науки РФ

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

«Уральский государственный педагогический университет»

Толстопятов В.П.

ГЕОМЕТРИЯ

Курс лекций 4 семестр

Учебное пособие

Екатеринбург

2012

Геометрия. Курс лекций, 4 семестр / Учебное пособие / Урал. гос. пед. ун-т. – Екатеринбург, 2012. – 84 с.

Толстопятов В.П., к.ф.-м.н., профессор кафедры геометрии УрГПУ

Уральский государственный

педагогический университет, 2012

СОДЕРЖАНИЕ

Раздел VIII. Дифференциальная геометрия 4

Раздел IX. Основания геометрии 27

Литература 71

Раздел VIII. Дифференциальная геометрия

Дифференциальная геометрия – это часть математики, которая изучает геометрические образы, в первую очередь кривые и поверхности, методами математического анализа. Другими словами, геометрические объекты – линии и поверхности – изучаются с точки зрения их строения в бесконечно малых кусках.

Лекция 1. Вектор-функция скалярного аргумента. Теоремы о вектор-функциях постоянной длины, постоянного направления и компланарных значений

§1. Векторные функции скалярного аргумента

Пусть – трехмерное евклидово векторное пространство над полемдействительных чисел;–числовой промежуток, то есть одно из множеств: вся числовая прямая, числовой луч с началом или без начала, числовой отрезок, числовой отрезок без одного или без двух концов.

Если задано отображение , то говорят, что заданавекторная функция скалярного аргумента .

Если в пространстве выбран базис, то имеем

или . Таким образом, задание векторной функции равносильно заданию тройки числовых функций.

Для векторных функций определены те же алгебраические операции, что и для обычных векторов: это сложение, вычитание, умножение на числовую функцию, скалярное, векторное и смешанное умножение. Вводятся они поточечно для функций с одной и той же область определения:

Пусть – предельная точка числового промежутка. Векторназывается пределом функциипри, еслипри.

Свойства предельного перехода:

Пусть , тогда

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

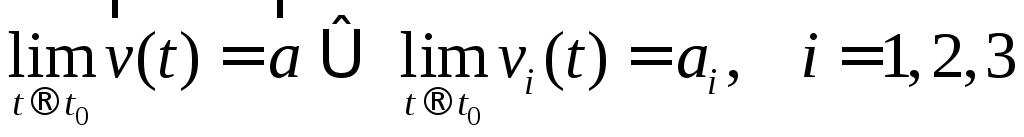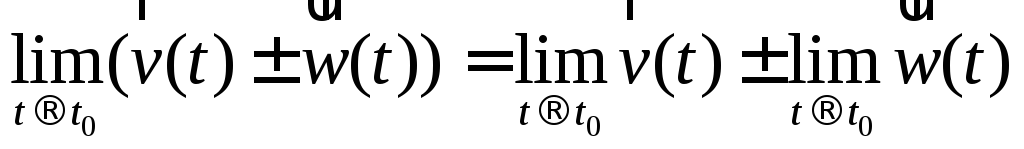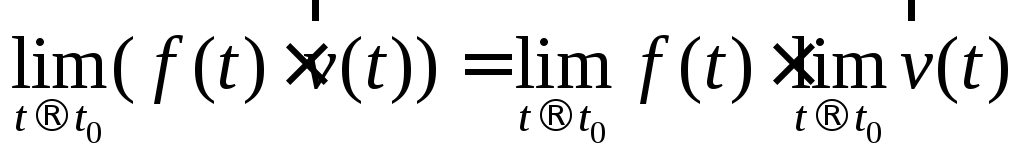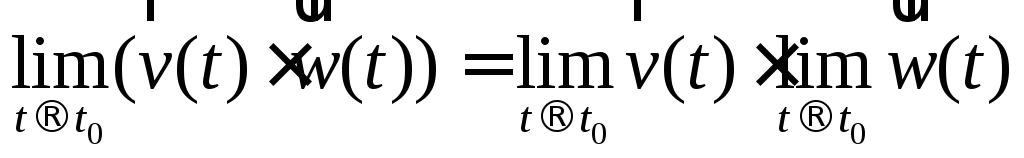при этом имеется ввиду, что все участвующие пределы существуют.

Векторная функция , определенная в точке, называетсянепрерывной в этой точке, если .

Векторная функция называется непрерывной, если она непрерывна в каждой точке области определения.

Простым следствием свойств предела являются следующие утверждения:

• Векторная функция непрерывна тогда и только тогда, когда непрерывны числовые координатные функции.

Если функции непрерывны, то непрерывны функции.

Векторная функция называетсядифференцируемой в точке , если присуществует предел отношения

. Этот предел называется производной векторной функции в точке и обозначается :

.

Если векторная функция имеет производную в каждой точке области определения, то она называется простодифференцируемой.

Свойства производной векторной функции аналогичны свойствам производной числовой функции.

Производная векторной функции может оказаться непрерывной и даже дифференцируемой, в этом случае можно говорить о производных векторной функции высшего порядка.

Для векторной функции , имеющей непрерывные производные до порядкавключительно на интервале, при любыхсправедливаформула Тейлора:

, где при.

Отметим наиболее часто встречающиеся теоремы.

Т е о р е м а 1. Производная векторной функции равна нулевому вектору тогда и только тогда, когда эта функция является постоянной векторной функцией: .

Т е о р е м а 2. (о векторной функции постоянной длины). Векторная функция имеет впромежутке постоянную длину тогда и только тогда, когда она ортогональна своей производной: .

Т е о р е м а 3. (о векторной функции постоянного направления). Векторная функция имеет в промежутке постоянное направление тогда и только тогда, когда в каждой точке этого промежутка значение векторной функции коллинеарно значению её производной:

(, где– постоянный орт).

Т е о р е м а 4. (о векторной функции, параллельной плоскости). Все значения векторной функции, заданной в промежутке , параллельны некоторой плоскости тогда и только тогда, когда в каждой точке этого промежутка значения векторной функции и её первой и второй производной компланарны: .

Для векторной функции по аналогии с числовыми функциями определяются понятия неопределенного и определенного интеграла.

Лекция 2. Понятие кривой. Гладкие кривые. Канонический репер. Формулы Серре-Френе §2. Понятие кривой

Пусть в евклидовом пространстве задана прямоугольная система координат.

Если – векторная функция, определенная на числовом промежутке, то.

Будем откладывать от начала системы координат. Конец вектора, который будем обозначать, будет иметь своим радиус-вектором

(1)

и своими координатами

(2).

Когда пробегает числовой промежуток, получаем множество точек, которое называетсягодографом векторной функции .

Элементарной кривой (элементарной линией) называется годограф взаимно однозначной непрерывной векторной функции , определенной на числовом промежутке.

В случае, когда числовой промежуток является отрезком, элементарная кривая называетсяпростой дугой.

Уравнение (1) называется векторным уравнением элементарной кривой, а уравнения (2) – параметрическими уравнениями элементарной кривой.

Примерами элементарных кривых являются:

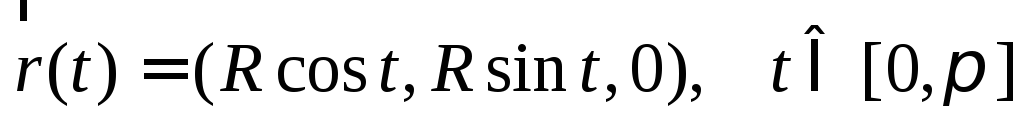1. –полуокружность;

2. –окружность;

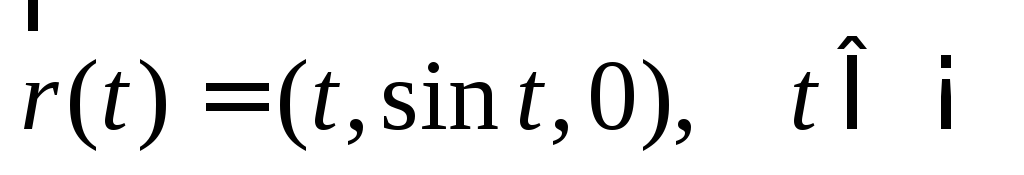3. –синусоида;

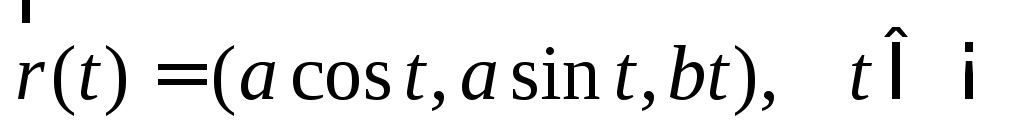4. –винтовая линия.

Линией или кривой называется фигура, которую можно представить как объединение конечного или счетного множества элементарных кривых.

Примерами кривых являются тангенсоида, гипербола, астроида.

§3. Гладкие кривые

Линия , заданная уравнением, называетсягладкой класса , еслиимеет непрерывные производные до порядкавключительно, причем.

Можно доказать, что вблизи каждой своей точки гладкая кривая является простой дугой.

Если – взаимно однозначное и взаимно непрерывное отображение числового промежуткана числовой промежуток, то имеем, и мы приходим к новой параметризации той же самой кривой:

.

Таким образом, одна и та же кривая допускает различные параметризации. Для гладкой кривой класса естественно считать допустимой такую замену параметра, когда функцияимеет непрерывные производные до порядкавключительно и первая производнаяво всех точках промежутка отлична от нуля, так как при такой замене новая параметризация снова дает гладкую кривую класса.

В дальнейшем мы будем рассматривать только гладкие кривые.

§4. Касательная к кривой

Пусть - гладкая кривая, заданная уравнением.

Зафиксируем точку и рассмотрим произвольную прямую, проходящую через эту точку. Пустьпроизвольная точка линии,– её расстояние до прямой.

Прямая называетсякасательной к линии в точке , если при стремлениикпо линииотношениестремится нулю.

Имеет место

Т е о р е м а. Гладкая кривая имеет в каждой своей точке касательную, причем единственную.

При доказательстве этой теоремы расстояние можно найти как длину вектораи использовать при этом формулу Тэйлора.

Расстояние можно найти как высоту параллелограмма, построенного на вектореи направляющем ортепрямой. Тоесть.

Тогда получим, что тогда и только тогда, когда, то есть направляющий орт касательнойколлинеарен вектору. Таким образом, направляющим вектором касательной к гладкой кривой в точкеявляется вектор.

§5. Длина кривой

В математическом анализе длина простой дуги гладкой кривой определяется как предел длины ломаной, вписанной в дугу, когда длина наибольшего звена ломаной стремится к нулю, и доказывается, что

.

Если точка разбивает отрезокна два отрезка так, что на каждом из нихопределяет простую дугу, то длина кривой равна сумме длин этих простых дуг. Тогда по свойствам интегралов получим длину гладкой кривой:

.

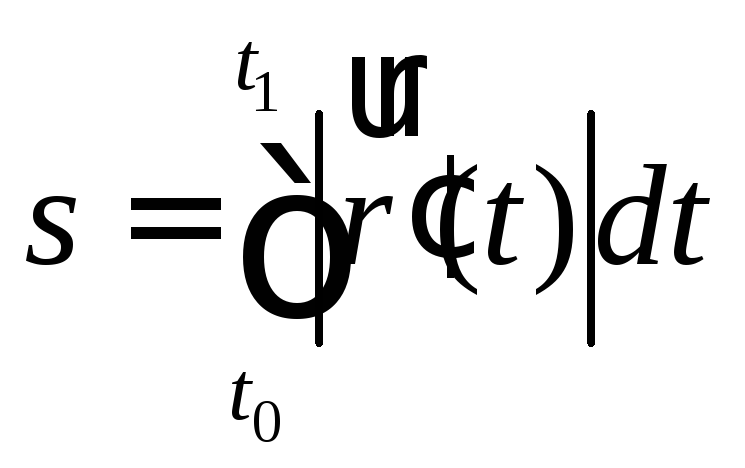Если второй конец дуги отвечает параметру , то получаем длину дуги как функцию этого параметра:

.

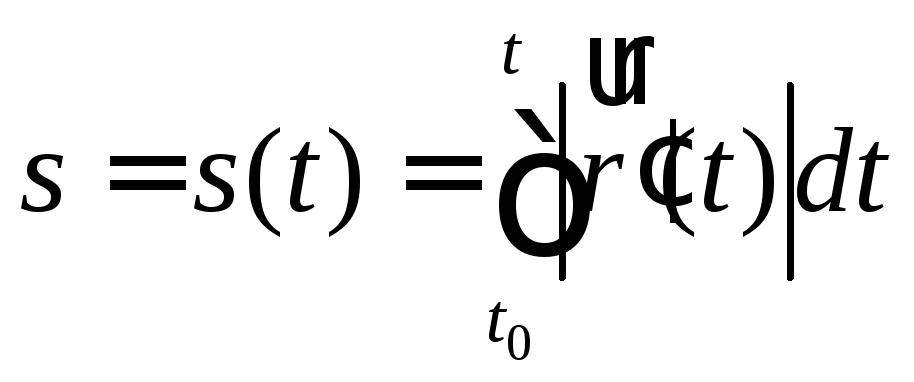Функция

1. непрерывна, так как непрерывна подинтегральная функция ;

2. монотонно возрастает, так как .

Следовательно, функция обратима в области её определения и функцияимеет непрерывные производные, отличные от нуля. Таким образом, имеем допустимую замену параметраили.

Новый параметр – длина дуги – называетсянатуральным (естественным) параметром.

Так как 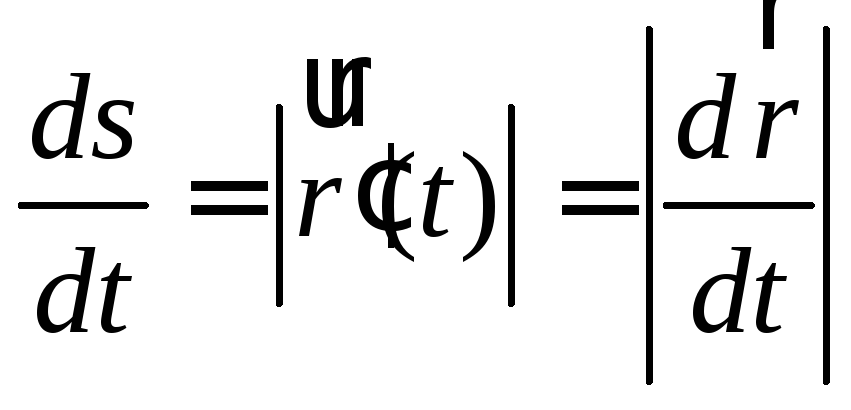, то в случае естественной параметризации имеем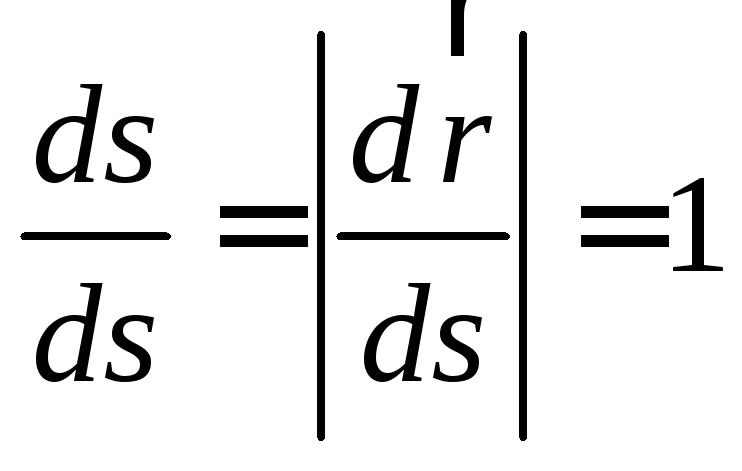, то есть вектор– единичный вектор. Так как векторявляется направляющим вектором касательной к линиив соответствующей точке, то его называютединичным вектором касательной к линии в точке и обозначают (в отличие от производных, берущихся по произвольному параметру, будем обозначать производную по натуральному параметру точкой).