
- •§2. Свободный вектор
- •§3. Сложение и вычитание свободных векторов
- •§4. Умножение свободного вектора на число
- •Лекция 2. Векторное пространство. Базис и координаты вектора §5. Понятие векторного пространства
- •§6. Линейная зависимость векторов
- •§7. Базис векторного пространства. Координаты вектора
- •Лекция 3. Скалярное умножение свободных векторов §8. Проекция вектора на вектор
- •§9. Скалярное умножение свободных векторов
- •Лекция 4 - 5. Векторное и смешанное умножение свободных векторов §10. Ориентация векторного пространства
- •§11. Векторное умножение свободных векторов
- •§12. Смешанное умножение свободных векторов
- •Раздел II. Аналитическая планиметрия Лекция 1. Аффинные системы координат на плоскости. Метод координат §1. Аффинная система координат на плоскости
- •§2. Формулы преобразования координат
- •§3. Метод координат на плоскости
- •Лекция 2. Прямая на плоскости как линия первого порядка §4. Уравнение прямой на плоскости
- •§5. Особенности расположения прямой относительно системы координат
- •Лекция 3. Аналитическое задание полуплоскостей. Вычисление расстояний и углов на плоскости §6. Геометрический смысл знака трехчлена прямой
- •§7. Расстояние от точки до прямой
- •§8. Взаимное расположение двух прямых на плоскости
- •§9. Угол между прямыми
- •Лекция 4. Конические сечения: эллипс, гипербола, парабола §10. Эллипс
- •§11. Гипербола
- •§12. Парабола
- •§13. Директориальное свойство эллипса и гиперболы
- •Лекция 5. Классификация линий второго порядка на плоскости §14. Приведение общего уравнения линии второго порядка к каноническому виду
- •Лекция 6. Общая теория линий второго порядка §15. Центр линии второго порядка
- •§16. Взаимное расположение линии второго порядка и прямой
- •§19. Диаметры линий второго порядка
- •§20. Главные направления, главные диаметры
- •Литература
§12. Парабола
О
п р е д е л е н и е. Параболой
называется множество всех точек
плоскости, расстояние от которых до
заданной прямой, называемой директрисой,
равно расстоянию до заданной точки –
фокуса:
![]() .
.
Расстояние
![]() от фокуса до директрисы называетсяфокальным
параметром параболы.
от фокуса до директрисы называетсяфокальным
параметром параболы.
По
аналогии с эллипсом и гиперболой
выводится каноническое
уравнение параболы:
![]() .
.
Изучение формы параболы
 –ось
симметрии параболы.
–ось
симметрии параболы.Точки
 принадлежат параболе.
принадлежат параболе.Поиск точек пересечения произвольной прямой проходящей через начало системы координат
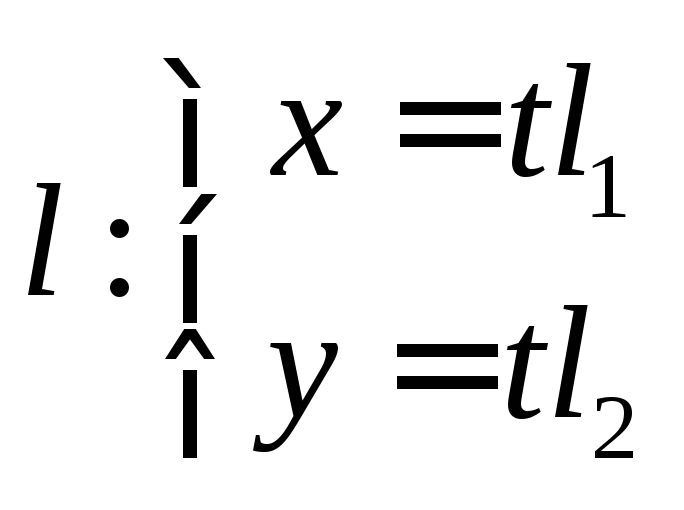 с параболой сводится к решению к решению
уравнения
с параболой сводится к решению к решению
уравнения .
Таким образом, если прямая
.
Таким образом, если прямая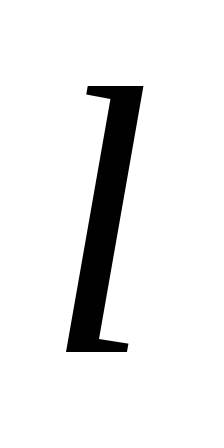 отлична от оси
отлична от оси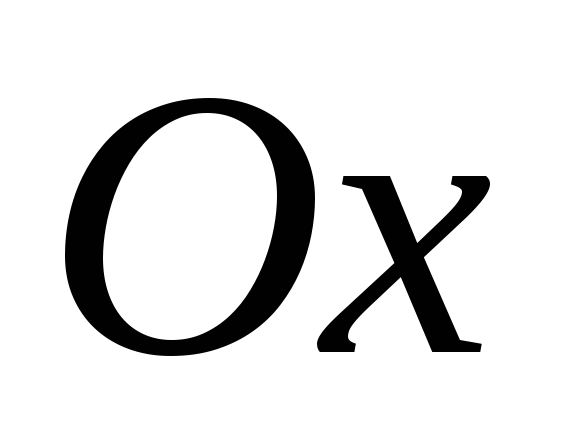 (
(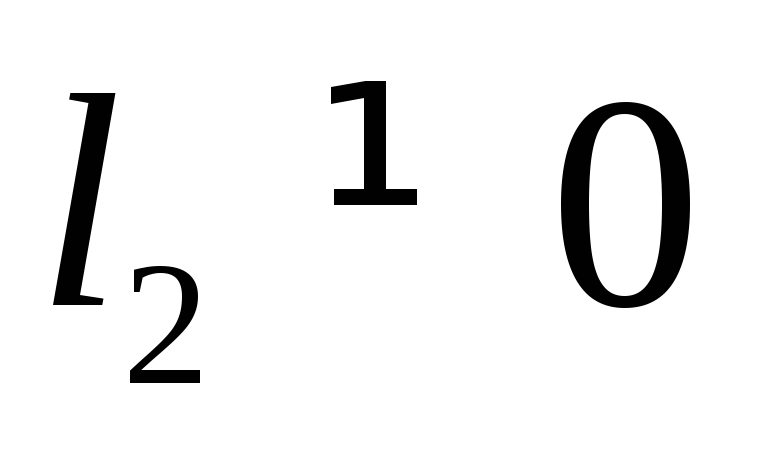 ),
то она пересекает параболу в двух
различных точках. Ось
),
то она пересекает параболу в двух
различных точках. Ось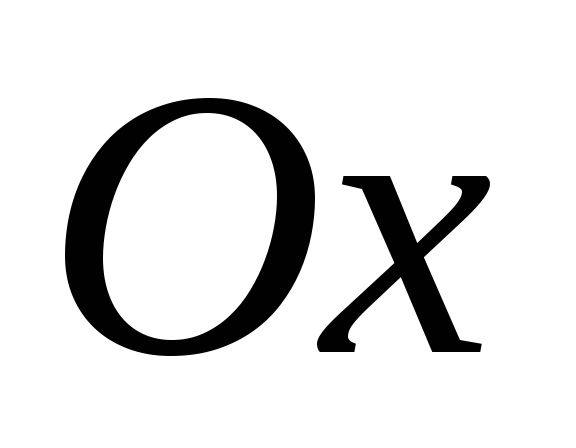 пересекает параболу в одной точке.
пересекает параболу в одной точке.
§13. Директориальное свойство эллипса и гиперболы
О
п р е д е л е н и е. Директрисой
эллипса (гиперболы)
называется прямая, перпендикулярная
фокальной оси и отстоящая от второй оси
на расстоянии
![]() .
.
Таким
образом, для эллипса (гиперболы), заданных
каноническими уравнениями
![]() ,
директрисы задаются уравнениями
,
директрисы задаются уравнениями![]() .
.
Имеет место следующая теорема
Т е о р е м а. Эллипс (гипербола) есть множество всех точек плоскости, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.
Д о к а з а т е л ь с т в о.Фактически требуется доказать совпадение двух множеств: эллипса (гиперболы) и множества точек, обладающих указанным в теореме свойством. Таким образом, достаточно показать включение каждого из этих множеств в другое.
Для любой точки
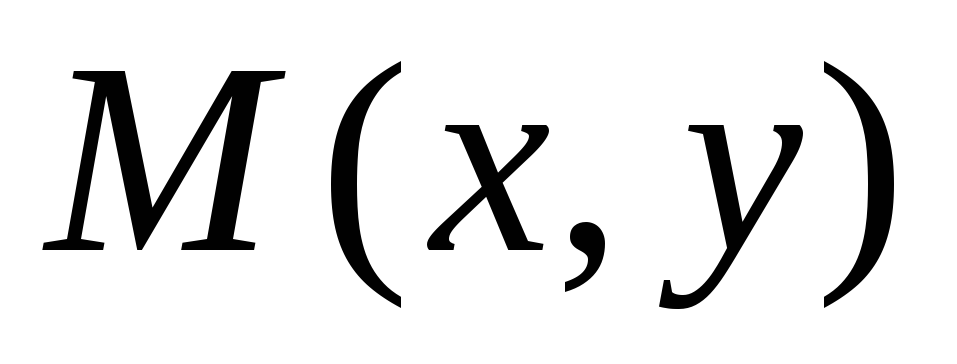 ,
принадлежащей эллипсу (гиперболе), её
координаты удовлетворяют уравнению
,
принадлежащей эллипсу (гиперболе), её
координаты удовлетворяют уравнению .
Кроме того, для этих линий соответственно
имеем соотношения:
.
Кроме того, для этих линий соответственно
имеем соотношения: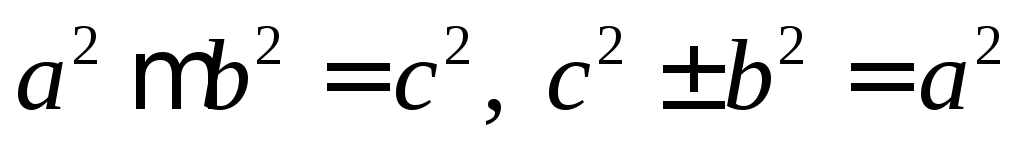 .
Учитывая это, можно подсчитать
.
Учитывая это, можно подсчитать .
Так как
.
Так как ,
то получаем
,
то получаем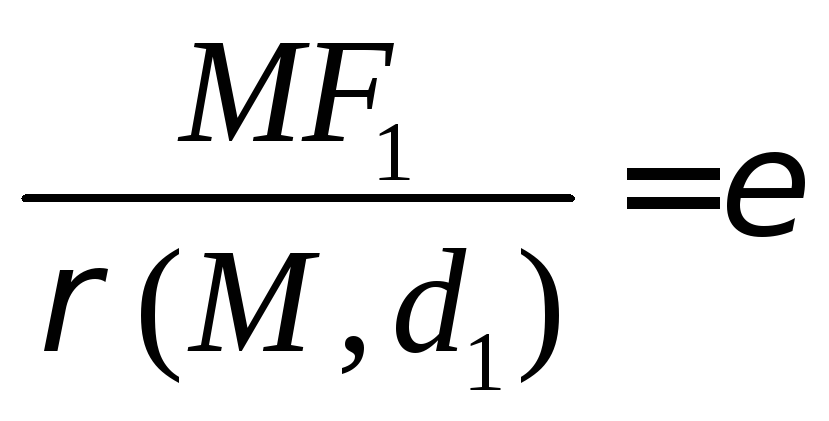 .
Таким образом, имеет место включение
всех точек эллипса (гиперболы) во
множество точек, отношение расстояний
от которых до фокуса к расстоянию до
соответствующей директрисы равно
эксцентриситету.
.
Таким образом, имеет место включение
всех точек эллипса (гиперболы) во
множество точек, отношение расстояний
от которых до фокуса к расстоянию до
соответствующей директрисы равно
эксцентриситету.Пусть для точки
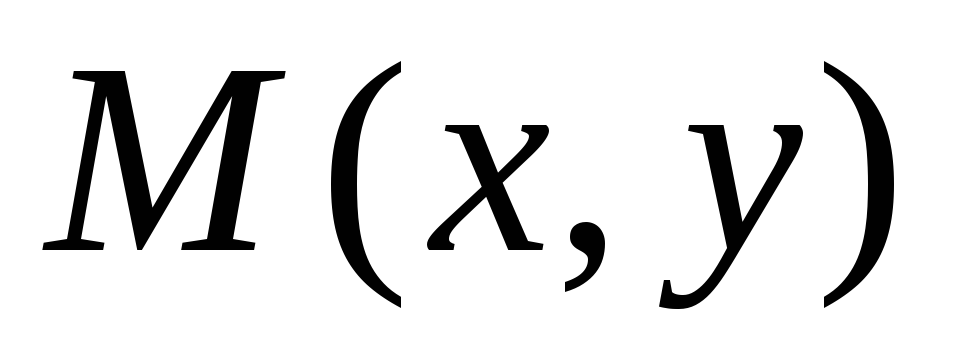 имеет место равенство
имеет место равенство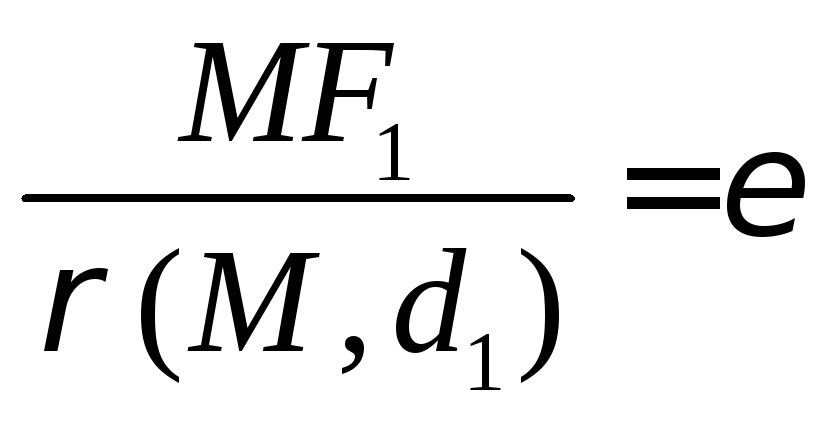 .
Получаем
.
Получаем или
или
![]() .(*)
.(*)
Если
![]() ,
то
,
то![]() и
и![]() .
Уравнение (*) определяет гиперболу
.
Уравнение (*) определяет гиперболу![]() .
То есть точка
.
То есть точка![]() принадлежит гиперболе.
принадлежит гиперболе.
Если
![]() ,
то
,
то![]() ,
,![]() и уравнение (*) определяет эллипс
и уравнение (*) определяет эллипс![]() .
То есть точка
.
То есть точка![]() принадлежит
эллипсу.
принадлежит
эллипсу.
Таким образом, для множества точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету, показали его включение во множество точек эллипса (гиперболы).
Из пунктов 1, 2 следует справедливость утверждения теоремы.
Лекция 5. Классификация линий второго порядка на плоскости §14. Приведение общего уравнения линии второго порядка к каноническому виду
Из
определения алгебраической линии
следует, что в произвольной аффинной
системе координат
![]() уравнение линии второго порядка имеет
вид:
уравнение линии второго порядка имеет
вид:
![]() ,
(1)
где
,
(1)
где
![]() –общее
уравнение алгебраической линии второго
порядка.
–общее
уравнение алгебраической линии второго
порядка.
Пусть
относительно прямоугольной системы
координат
![]() линия второго порядка задана уравнением
(1).
линия второго порядка задана уравнением
(1).
Т е о р
е м а. Для
каждой линии второго порядка, заданной
в прямоугольной системе координат
уравнением (1), существует прямоугольная
система координат
![]() ,
в которой линия задается уравнением
вида
,
в которой линия задается уравнением
вида
![]() (2).
(2).
Д о к а
з а т е л ь с т в о. Имеем формулы
преобразования координат при повороте
осей координат на угол
![]()
![]() (3)
(3)
Чтобы
найти уравнение линии в новой системе
координат, нужно в уравнение (1) подставить
выражения (3) старых координат через
новые. Будем искать такой угол
![]() поворота осей координат, чтобы в новом
уравнении коэффициент при
поворота осей координат, чтобы в новом
уравнении коэффициент при![]() был равен нулю:
был равен нулю:
![]() .
(4)
.
(4)
В
уравнении (4)
![]() .
В противном случае, получим
.
В противном случае, получим![]() ,
то есть уравнение (1) уже имеет требуемый
вид.
,
то есть уравнение (1) уже имеет требуемый
вид.
Из
однородного уравнения (4) находим два
значения угла
![]() ,
для которых коэффициент при произведении
текущих координат обращается в нуль.
Можно выбрать любой из них. При повороте
осей координат системы
,
для которых коэффициент при произведении
текущих координат обращается в нуль.
Можно выбрать любой из них. При повороте
осей координат системы![]() на этот угол получим искомый репер
на этот угол получим искомый репер![]() .
.
Пусть уравнение линии второго порядка приведено к виду (2). Возможны случаи
I.
![]() .
.
Выделив
для
![]() и
и![]() полные квадраты, получим уравнение вида
полные квадраты, получим уравнение вида
![]() ,
(5)
,
(5)
где
обозначено
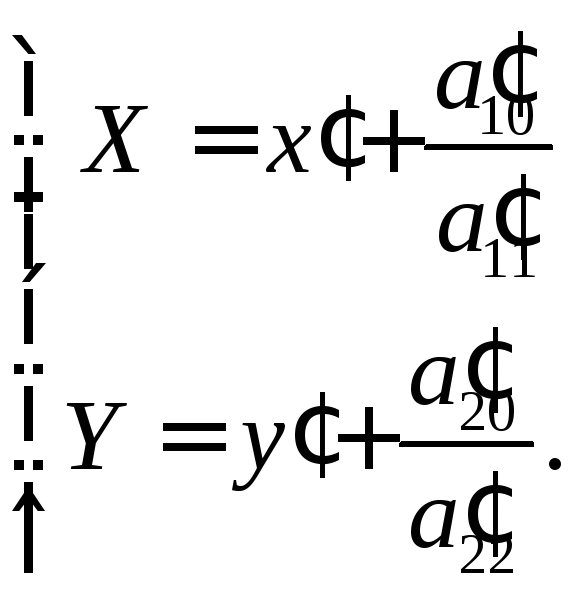
Отсюда
получаем
 – формулы преобразования координат
при переносе начала системы координат
в точку
– формулы преобразования координат
при переносе начала системы координат
в точку![]() .
.
В
зависимости от значений параметров
![]() можно получить следующие канонические
уравнения
можно получить следующие канонические
уравнения
|
|
|
|
Каноническое уравнение |
Название линии |
|
+ |
+ |
- |
|
Эллипс |
|
- |
- |
+ | ||
|
+ |
+ |
+ |
|
Мнимый эллипс |
|
- |
- |
- | ||
|
+ |
- |
|
|
Гипербола |
|
- |
+ | |||
|
+ |
+ |
0 |
|
Пара мнимых пересекающихся прямых |
|
- |
- | |||
|
+ |
- |
0 |
|
Пара пересекающихся прямых |
|
- |
+ |
II.
![]() .
.
Уравнение (2) можно записать в виде
![]() .
.
Обозначив
![]() ,
,![]() ,
получим каноническое уравнение параболы:
,
получим каноническое уравнение параболы:![]() .
.
III.
![]() .
.
Уравнение
линии приводится к виду
![]() .
В зависимости от значений параметра
.
В зависимости от значений параметра![]() получаем каноническое уравнение пары
параллельных прямых, пары совпавших
прямых, пары мнимых параллельных прямых.
получаем каноническое уравнение пары
параллельных прямых, пары совпавших
прямых, пары мнимых параллельных прямых.
Таким образом, имеем 9 сортов линий второго порядка.
Чтобы привести уравнение линии второго порядка к каноническому виду, надо:
добиться, чтобы в группе старших членов исчез член с произведением текущих координат (поворот осей координат);
добиться, чтобы число членов первой степени стало наименьшим (выделение полных квадратов, перенос начала системы координат);
если возможно, уничтожить свободный член (перенос начала системы координат).
