- •Математика
- •Оглавление
- •Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки. Тема 1. Функции одной переменной. Предел функции
- •Решение типовых примеров.
- •Тема 2. Производная и дифференциал функции
- •Правила дифференцирования
- •Производная сложной функции
- •Решение типовых примеров
- •Тема 3. Неопределенный интеграл
- •3. Таблица основных дифференциалов функции
- •4 Таблица интегралов.
- •5. Основные методы интегрирования.
- •Непосредственное интегрирование.
- •Замена переменной (интегрирование подстановкой).
- •Интегрирование по частям.
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Тема 4. Определенный интеграл.
- •Геометрический смысл определенного интеграла.
- •Задачи к теме 1. Функции одной переменной. Предел функции
- •Задачи к теме 2. Производная и дифференциал функции
- •Задачи к теме 3. Неопределенный интеграл
- •Задачи к теме 4. Определенный интеграл.
- •Список литературы
- •Приложение 1 Образец оформления титульного листа
- •Контрольная работа №2 по дисциплине «математика»
- •2011 Приложение 2 Справочный материал по элементарной математике
- •Математика
Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки. Тема 1. Функции одной переменной. Предел функции
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов нахождения пределов различных видов.
Определение
1.Число А называется пределом
функции
![]() при
при![]() стремящимся к бесконечности(
стремящимся к бесконечности(![]() ),
если для любого, сколь угодно малого
положительного числа
),
если для любого, сколь угодно малого
положительного числа![]() ,
найдется такое положительное число
,
найдется такое положительное число![]() (зависящее
от
(зависящее
от![]() ;
;![]() ),
что для всех
),
что для всех![]() таких, что
таких, что![]() ,
верно неравенство:
,
верно неравенство:![]() .
.
Этот предел
обозначается
![]() .
.
Определение
2.Число А называется пределом
функции
![]() при
при![]() стремящимся к
стремящимся к![]() или в точке
или в точке ![]() (
(![]() ),
если для любого, даже сколь угодно малого
положительного числа
),
если для любого, даже сколь угодно малого
положительного числа![]() ,
найдется такое положительное число
,
найдется такое положительное число![]() (зависящее
от
(зависящее
от![]() ;
;![]() ),
что для всех
),
что для всех![]() ,
не равных
,
не равных![]() (
(![]() )
и удовлетворяющих условию
)
и удовлетворяющих условию![]() , выполняется неравенство:
, выполняется неравенство:![]() .
.
Этот предел
обозначается
![]() .
.
Рассмотрим
предел:![]() ,
он состоит из трех частей:
,
он состоит из трех частей:
значка предела
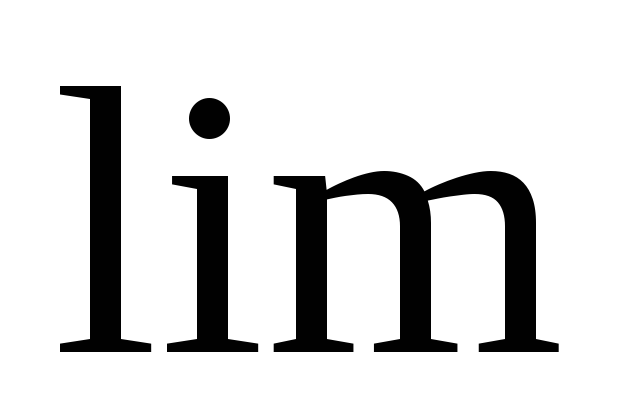 ;
;записи под значком предела:
 .
Запись читается «икс стремится к
семи». В практических заданиях на
месте семи может находиться совершенно
любое число, а также бесконечность (
.
Запись читается «икс стремится к
семи». В практических заданиях на
месте семи может находиться совершенно
любое число, а также бесконечность ( );
);функции под знаком предела, в данном случае
 .
.
Сама запись
![]() читается так: «предел функции
читается так: «предел функции
![]() при икс стремящемся к семи».
при икс стремящемся к семи».
Как решить
вышерассмотренный пример? Исходя из
вышесказанного, нужно просто подставить
число семь в функцию, стоящую под знаком
предела:
![]() , поскольку в точке
, поскольку в точке![]() ,
функция, стоящая под знаком предела
непрерывна и предел равен значению
функции в этой точке (так как это значение
существует).
,
функция, стоящая под знаком предела
непрерывна и предел равен значению
функции в этой точке (так как это значение
существует).
Итак, первое
правило: когда дан предел,
сначала просто вместо
![]() подставить число, к которому
подставить число, к которому![]() стремится и найти значение функции при
этом
стремится и найти значение функции при
этом![]() .Если получилось число, то предел будет
равен полученному числу. Если получились
выражения (неопределенности) типа
.Если получилось число, то предел будет
равен полученному числу. Если получились
выражения (неопределенности) типа![]() или
или![]() ,
то необходимо произвести тождественные
преобразования выражения, стоящего под
знаком предела, чтобы избавиться от
этих неопределенностей.
,
то необходимо произвести тождественные
преобразования выражения, стоящего под
знаком предела, чтобы избавиться от
этих неопределенностей.
При
этом можно
использовать основные правила вычисления
пределов.
Пусть существуют
![]() .
Тогда
.
Тогда
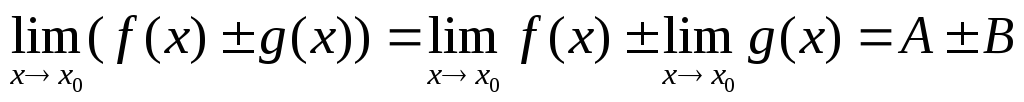 .
.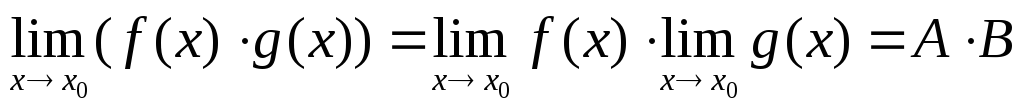 .
.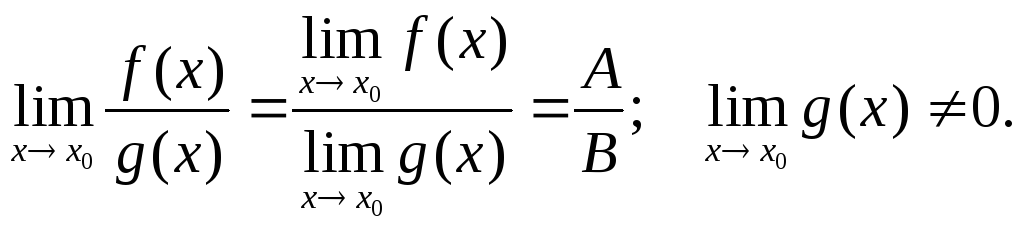
 ,
где с– постоянный множитель,с
=const.
,
где с– постоянный множитель,с
=const.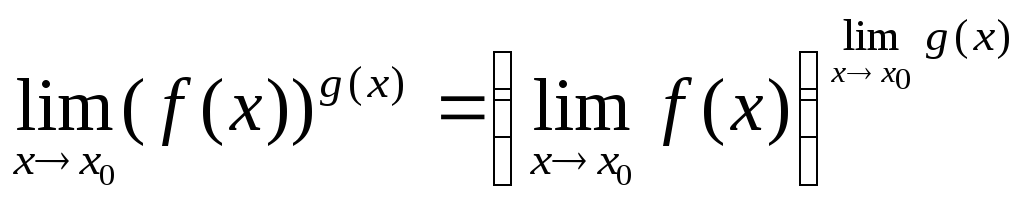 ,
,
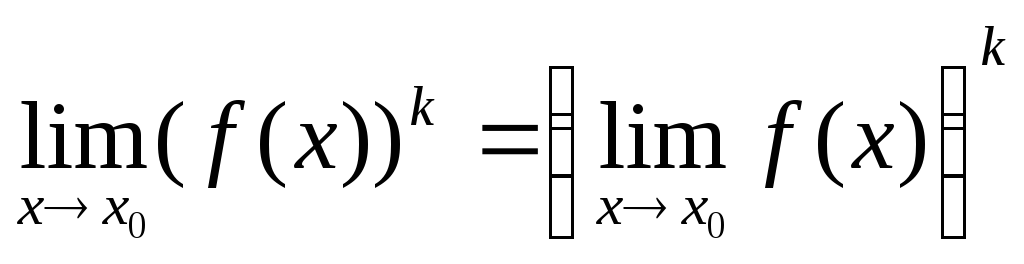 ,
,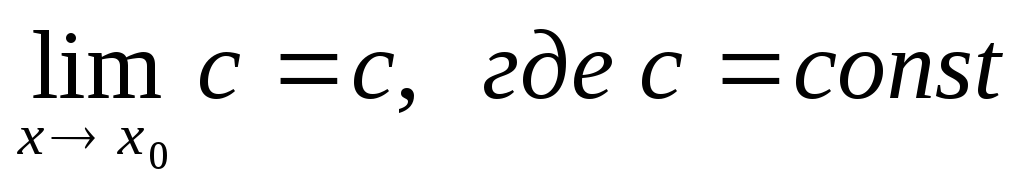
первый замечательный предел:

Следствия из первого замечательного предела:
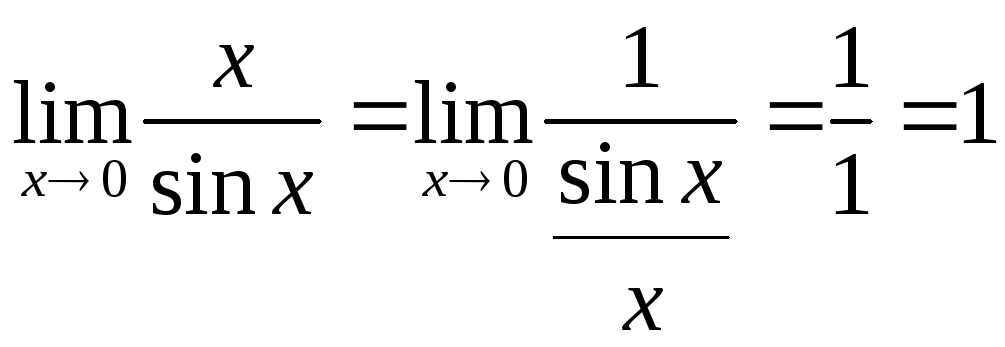
![]()
![]() ,
где α=const.
,
где α=const.
второй замечательный предел:
 и
и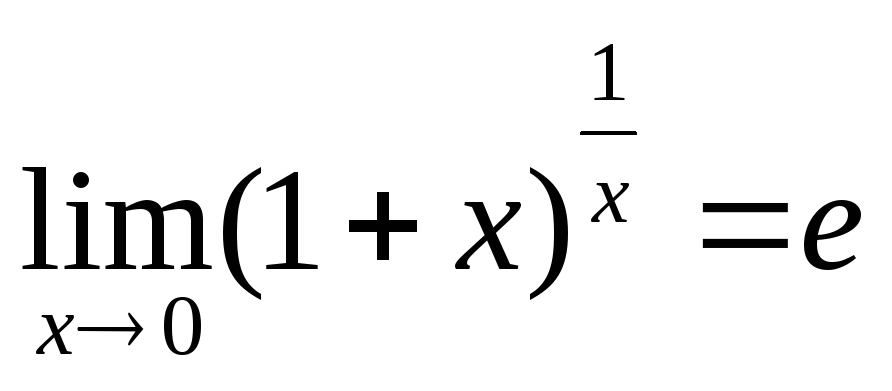
е 2,7182… или е2,7
пределы бесконечно больших и малых функций
Если
 .
.
|
|
|
эквивалентные бесконечно малые функции
Если
![]()
![]()
![]() ,
тогда
,
тогда![]() .
.
|
|
Решение типовых примеров.
Задача 1. Вычислить
предел:
![]() .
.
При
подстановке в выражение![]()
![]() под знаком предела получаем
неопределенность вида
под знаком предела получаем
неопределенность вида![]() .
Используя эквивалентные бесконечно
малые функции, получаем:sin3x~ 3x, tg7x~ 7x,
.
Используя эквивалентные бесконечно
малые функции, получаем:sin3x~ 3x, tg7x~ 7x,![]() ~
3x2. Тогда
~
3x2. Тогда
![]()
Задача 2. Вычислить
предел:
![]() .
.
При
подстановке в выражение![]()
![]() под знаком предела получаем
неопределенность вида
под знаком предела получаем
неопределенность вида![]() .
Используя эквивалентные бесконечно
малые функции, получаем:sin(x-1)
~ (x-1), так как
.
Используя эквивалентные бесконечно
малые функции, получаем:sin(x-1)
~ (x-1), так как![]() .
Тогда
.
Тогда
![]()
Задача 3. Вычислить
предел:
![]() .
.
При
подстановке в выражение![]()
![]() под знаком предела получаем
неопределенность вида
под знаком предела получаем
неопределенность вида![]() .
Значит, функция
.
Значит, функция
![]() не определена в точке
не определена в точке
![]() .Произведем
тождественные преобразованиявыражения, стоящего под знаком предела,
не принимая во внимание его поведения
в предельной точке.
.Произведем
тождественные преобразованиявыражения, стоящего под знаком предела,
не принимая во внимание его поведения
в предельной точке.
В числителе и
знаменателе
![]() находятся
квадратные трехчлены. Разложим
квадратные трехчлены, входящие в
числитель и знаменатель, на линейные
множители по формуле:
находятся
квадратные трехчлены. Разложим
квадратные трехчлены, входящие в
числитель и знаменатель, на линейные
множители по формуле:![]() ,
где х1и х2– корни квадратного
уравнения
,
где х1и х2– корни квадратного
уравнения![]() .
.
Разложим трехчлен
![]() на множители. Для этого:
на множители. Для этого:
1. Решим уравнение
![]()
![]() ,
,
![]() ,
,![]()
![]() ;
; ![]()
![]()
![]()
![]() ;
;![]()
2. Воспользуемся
формулой разложения квадратного
трехчлена на множители:![]()
![]()
Аналогично разложим трехчлен, стоящий в знаменателе на множители:
![]()
Преобразуем данный предел:
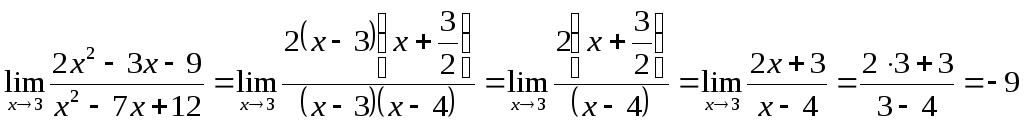
Ответ:![]()
Задача 4. Вычислить
предел![]()
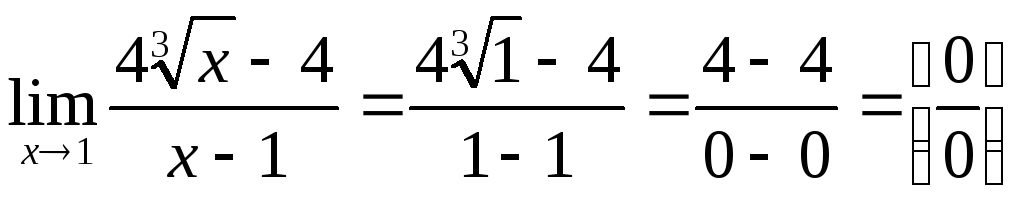
Для раскрытия неопределенности
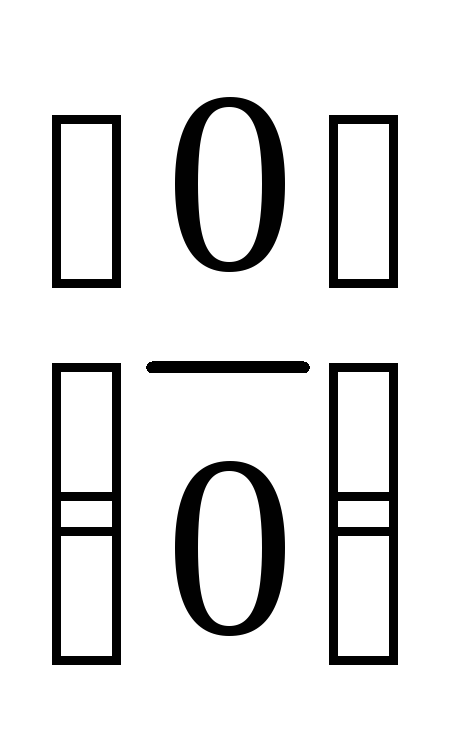 разложим знаменатель по формуле разности
кубов:
разложим знаменатель по формуле разности
кубов: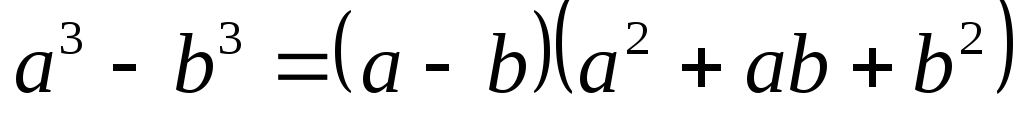 .
.
![]() ,
а в числителе вынесем общий множитель.
,
а в числителе вынесем общий множитель.
Ответ:![]() .
.
Задача 5.Вычислить предел![]()
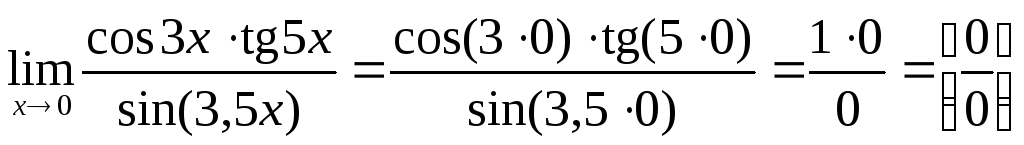
Для раскрытия неопределенности вида
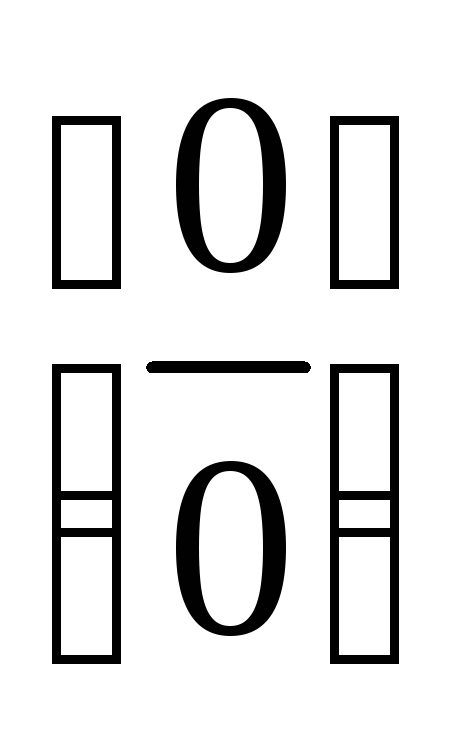 в данном примере воспользуемся первым
замечательным пределом и одним из его
следствий:
в данном примере воспользуемся первым
замечательным пределом и одним из его
следствий: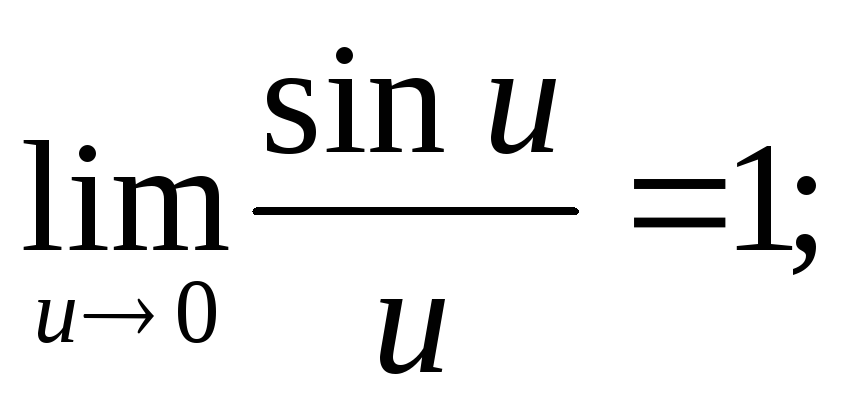
 ,
,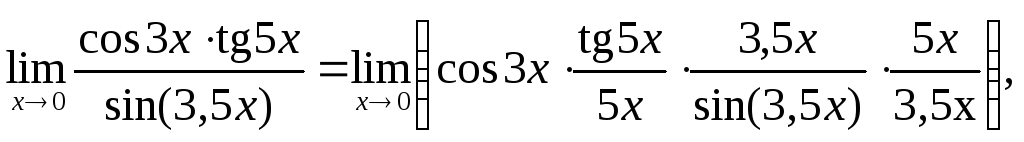
Заменим предел произведения функций произведением пределов этих функций и вынесем постоянный множитель:
![]() Ответ:
Ответ:
![]() .
.
Задача 6. Вычислить
предел
![]() .
.
Опять начинаем
увеличивать
![]() до бесконечности, и смотрим на
поведение функции: она растет. Поэтому
до бесконечности, и смотрим на
поведение функции: она растет. Поэтому
![]() .
.
Запомните следующие пределы:
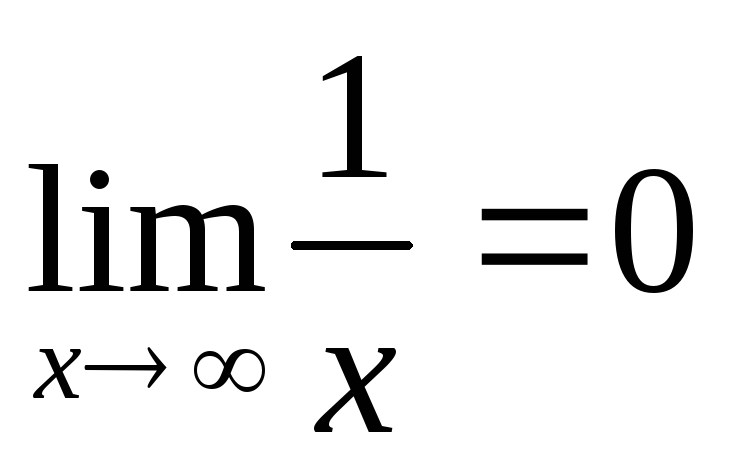 .
2.
.
2.
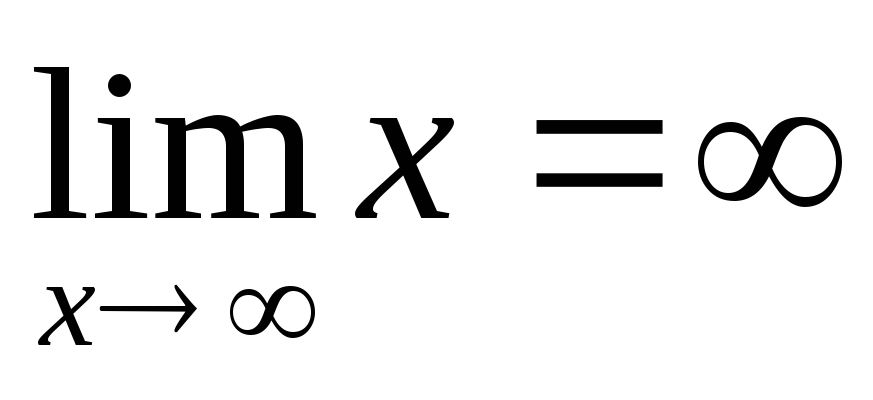 .
3.
.
3.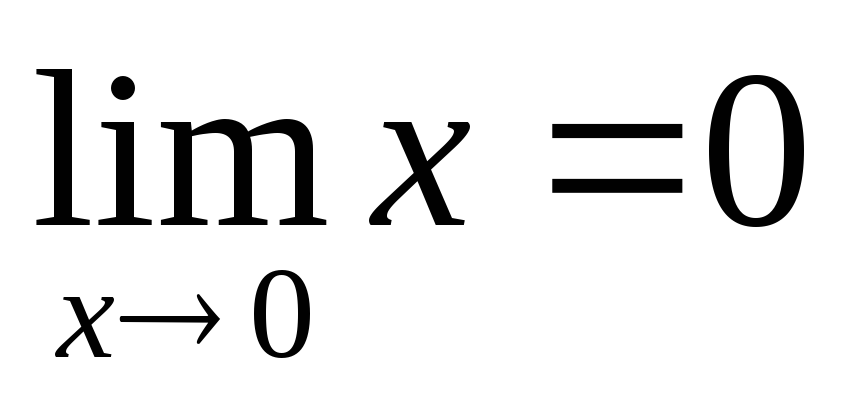 .
.
Пределы
с неопределенностью вида
![]() и
метод их решения.
и
метод их решения.
Рассмотрим группу
пределов, когда
![]() ,
а функция представляет собой дробь, в
числителе и знаменателе которой находятся
многочлены
,
а функция представляет собой дробь, в
числителе и знаменателе которой находятся
многочлены
Задача 7. Вычислить
предел![]()
Согласно нашему
правилу попытаемся подставить
бесконечность в функцию. Что у нас
получается в числителе? Бесконечность.
А что получается в знаменателе? Тоже
бесконечность. Таким образом, имеем
неопределенность вида
![]() .
Учитывая, что поведение числителя и
знаменателя при
.
Учитывая, что поведение числителя и
знаменателя при![]() определяется членами с наибольшими
показателями степеней (
определяется членами с наибольшими
показателями степеней (![]() в числителе и
в числителе и![]() в знаменателе), то для решения подобных
примеров надо разделить числитель и
знаменатель на старшую степень числителя
и знаменателя, в нашем случае
в знаменателе), то для решения подобных
примеров надо разделить числитель и
знаменатель на старшую степень числителя
и знаменателя, в нашем случае![]() .
Получим:
.
Получим:
 т.к.
т.к.
![]()
![]()
Ответ:![]()