
- •Математика
- •Оглавление
- •Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки. Тема 1. Функции одной переменной. Предел функции
- •Решение типовых примеров.
- •Тема 2. Производная и дифференциал функции
- •Правила дифференцирования
- •Производная сложной функции
- •Решение типовых примеров
- •Тема 3. Неопределенный интеграл
- •3. Таблица основных дифференциалов функции
- •4 Таблица интегралов.
- •5. Основные методы интегрирования.
- •Непосредственное интегрирование.
- •Замена переменной (интегрирование подстановкой).
- •Интегрирование по частям.
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Тема 4. Определенный интеграл.
- •Геометрический смысл определенного интеграла.
- •Задачи к теме 1. Функции одной переменной. Предел функции
- •Задачи к теме 2. Производная и дифференциал функции
- •Задачи к теме 3. Неопределенный интеграл
- •Задачи к теме 4. Определенный интеграл.
- •Список литературы
- •Приложение 1 Образец оформления титульного листа
- •Контрольная работа №2 по дисциплине «математика»
- •2011 Приложение 2 Справочный материал по элементарной математике
- •Математика
Интегрирование рациональных дробей
Рациональная
дробь– это отношение двух многочленов![]() ,
где
,
где![]() ,–многочлены
степенейnиmсоответственно.
Если степень многочлена в числителе
строго меньше степени многочлена
в знаменателе (n<m), то
дробь называетсяправильной. В
противном случае (nm) дробьнеправильная, она
представляется в виде суммы некоторого
многочлена и правильной рациональной
дроби.
,–многочлены
степенейnиmсоответственно.
Если степень многочлена в числителе
строго меньше степени многочлена
в знаменателе (n<m), то
дробь называетсяправильной. В
противном случае (nm) дробьнеправильная, она
представляется в виде суммы некоторого
многочлена и правильной рациональной
дроби.
Простейшими дробями называются правильные дроби следующего вида:
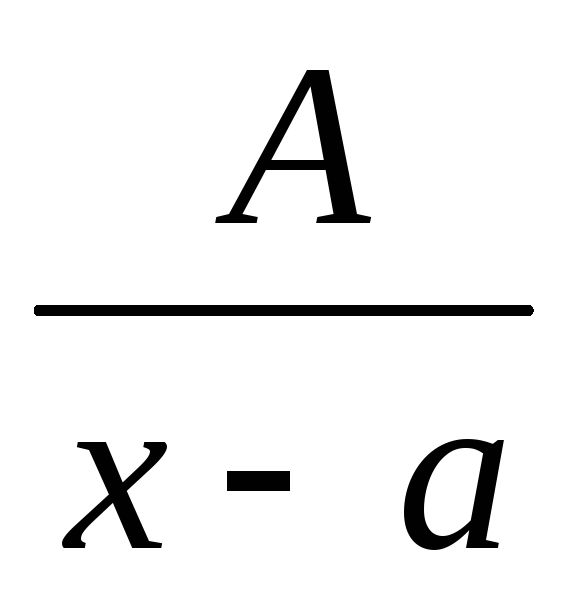
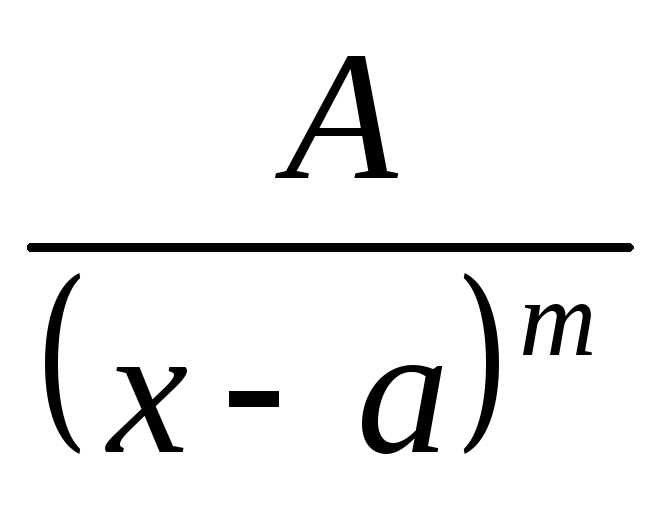 ,
где m– натуральное
число иm>1
,
где m– натуральное
число иm>1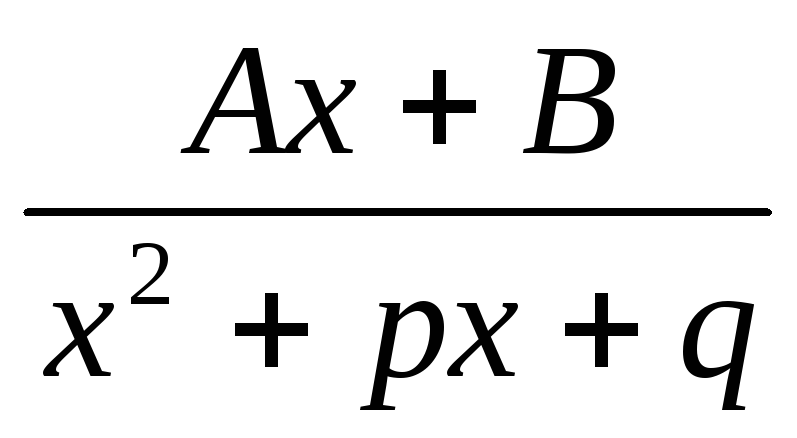 ,
где
,
где
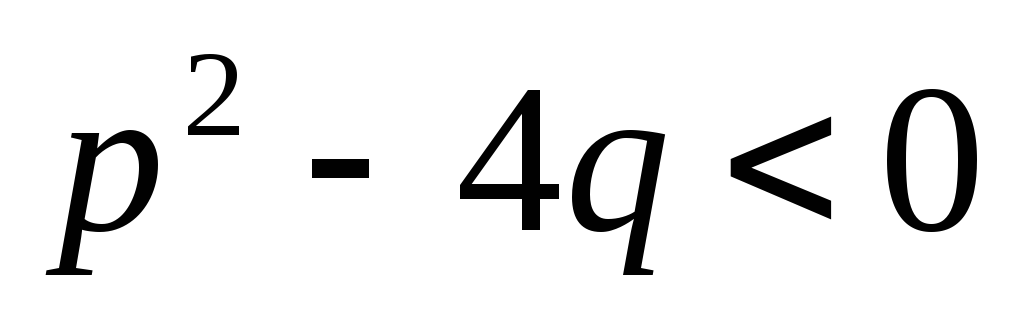 ,
т.е. квадратный трехчлен в знаменателе
не имеет действительных корней
,
т.е. квадратный трехчлен в знаменателе
не имеет действительных корней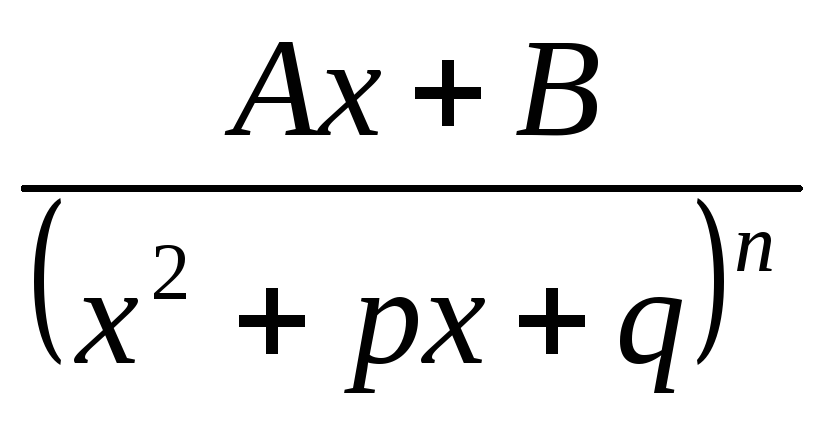 ,
где n– натуральное число,n>1 и квадратный трехчлен
в знаменателе не имеет действительных
корней.
,
где n– натуральное число,n>1 и квадратный трехчлен
в знаменателе не имеет действительных
корней.
Во все четырех случаях предполагается, что A,B,p,q,a– действительные числа.
Для интегрирования
рациональной функции
![]() используется следующая последовательность
шагов:
используется следующая последовательность
шагов:
Шаг 1. Преобразование неправильной рациональной дроби
Если дробь
неправильная (т.е. степень числителя
P(x)
больше степени знаменателяQ(x)),
разделим многочленP(x)
наQ(x).
Получим следующее выражение:![]() ,
гдеM(x) –
многочлен, а
,
гдеM(x) –
многочлен, а![]() – правильная рациональная дробь.
– правильная рациональная дробь.
Шаг 2. Разложение знаменателя на множители
Запишем многочлен
знаменателя Q(x) в виде:![]() ,
где
,
где![]() ,
т.е. квадратный трехчлен
,
т.е. квадратный трехчлен![]() не имеет действительных корней .
не имеет действительных корней .
Шаг 3. Разложение рациональной дроби на сумму простейших дробей.
Запишем рациональную функцию в следующем виде:
![]()
Общее число неопределенных коэффициентов Ai,Bi,Сiдолжно быть равно степени знаменателяQ(x). Затем умножим обе части полученного уравнения на знаменательQ(x) и приравняем коэффициенты при слагаемых с одинаковыми степенямиx. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентовAi,Bi,Сi . Данная система всегда имеет единственное решение. Описанный алгоритм представляет собойметод неопределенных коэффициентов.
Шаг 4. Интегрирование простейших рациональных дробей.
Рассмотрим интегралы от простейших дробей первых трех типов:
Тогда
![]() .
В первом интеграле числитель является
производной знаменателя, поэтому
.
В первом интеграле числитель является
производной знаменателя, поэтому![]() .
.
При разложении простейших дробей возможны ситуации:
если числитель является производной знаменателя, то интеграл равен логарифму натуральному от знаменателя:
![]()
квадратный трехчлен в знаменателе можно разложить на линейные множители, а подынтегральную функцию на простые рациональные дроби:
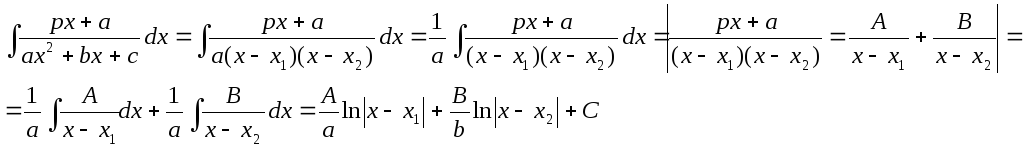
Коэффициенты А и В находят методом неопределенных коэффициентов.
квадратный трехчлен в знаменателе нельзя разложить на линейные множители, тогда следует выделить полный квадрат и ввести замену:
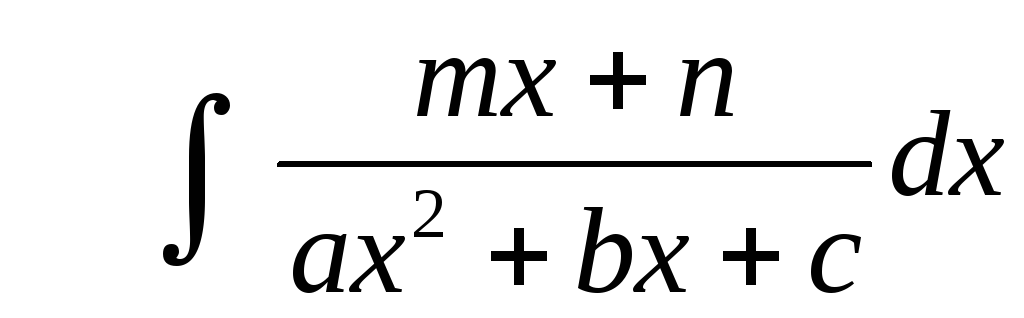
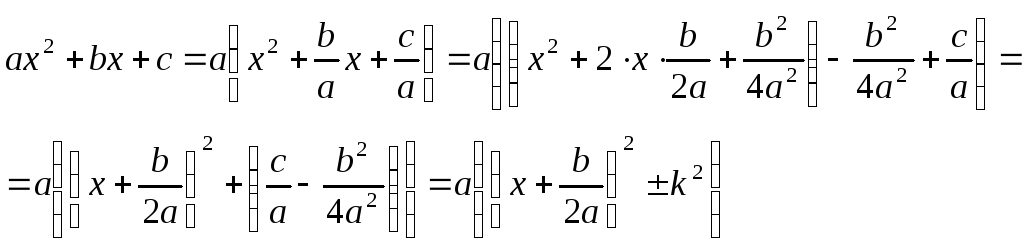
После чего вводят
новую переменную:
![]()
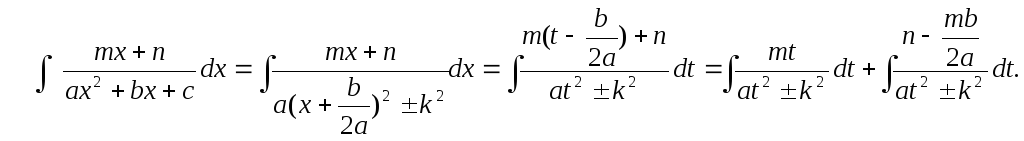
Эти интегралы можно вычислить: первый – подведением под знакдифференциала, второй –непосредственным интегрированием.
Задача 13. Найти
неопределенный интеграл![]() .
.
Решение.
Так как
![]() ,
то используем метод замены переменной.
,
то используем метод замены переменной.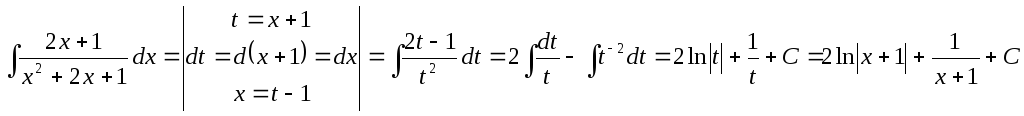 Задача 14. Найти неопределенный интеграл
Задача 14. Найти неопределенный интеграл![]() .
.
Решение.
Так как
![]() ,
то используем метод замены переменной.
,
то используем метод замены переменной.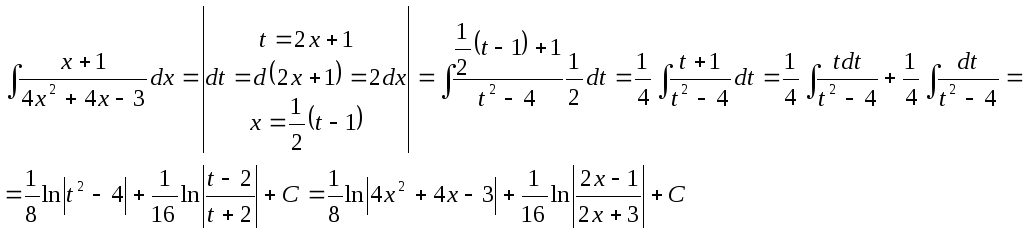 Задача
15. Найти неопределенный интеграл
Задача
15. Найти неопределенный интеграл![]() .
.
Решение.
Так как
![]() ,
то используем метод замены переменной.
,
то используем метод замены переменной.
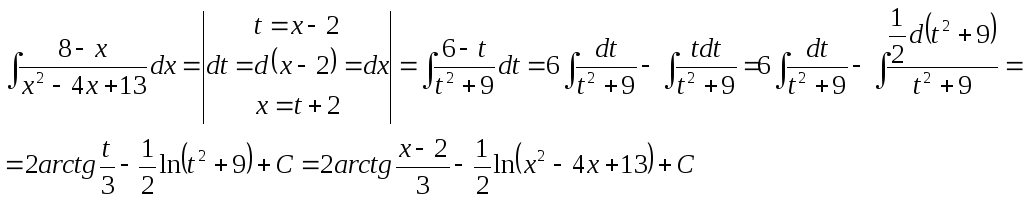
Задача 16. Найти
неопределенный интеграл![]() .
.
Решение.
Так как
![]() ,
то разложим рациональную дробь на сумму
простейших дробей и применимметоднеопределенных коэффициентов:
,
то разложим рациональную дробь на сумму
простейших дробей и применимметоднеопределенных коэффициентов:
![]()
Из последнего равенства найдем постоянные коэффициенты А1,А2,А3. Приводя дроби в правой части к общему знаменателю, приходим к равенству:
![]()
Теперь избавляемся от знаменателей, т.к. они одинаковы:
![]() .
.
В левой части раскрываем скобки:
![]() .
.
Сгруппируем по степеням x, вынесем общий множитель за скобки:
![]()
![]()
Составляем систему линейных уравнений из коэффициентов левой и правой части при соответствующих степенях x.
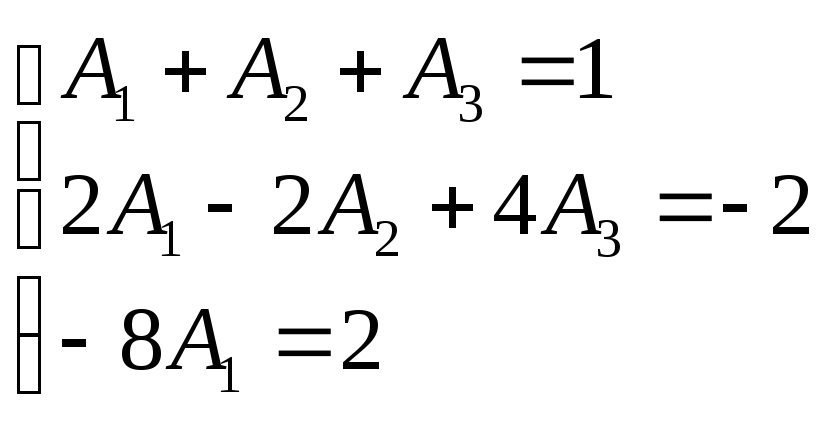
Решаем систему
уравнений и получаем ответ:
![]()
Тогда
![]() .
.
