Analiticheskaya_Geometria

Если уравнение плоскости является неполным (A = 0 или B = 0 ), то,
рассуждая аналогичным образом, получим уравнение (1.15), в котором со-
ответственно A = 0 или B = 0 .
		1.8. Преобразование прямоугольных координат
Пусть дана точка M(x, y)					на плоскости Oxy . Перенесем начало пря-
							′
моугольной системы координат в точку O (a,b) , где (a,b) − координаты но-
вого начала в старой системе координат Oxy .
		y				′
						y
		My			M′y				M
		O′y			O	′			Mx′	′
										x
		O			Ox′				Mx	x
Тогда			′	′		′	′		′	′	′
		x = OMx = OOx		+OxMx = OOx			+O Mx		= a + x ,	y = OMy = OOy +OyMy =
′	′ ′	′	, или
= OOy +O My = b + y
				′		′					(1.16)
				x = x − a ,		y = y −b .
Выражение (1.16) называется формулой преобразования координат
при параллельном переносе осей.										′ ′
Рассмотрим прямоугольную систему координат Ox y , полученную из
Oxy поворотом на угол α .
				y					M
		′	My
		y
										′
										x
			M′y						Mx′
							α	θ		x
				O					Mx
Из	треугольников			OMMx	и OMyM имеем:					OMx = OM cosθ ,	OMy =
= OM sinθ . Из треугольников OMMx′						и OM′yM
OMx′ = OM cos(θ −α) = OM(cosθ cosα +sinθ sinα) = OMx cosα +OMy sinα ,
						14

OM′y = OM sin(θ −α) = OM(sinθ cosα −cosθ sinα) = OMy cosα −OMx sinα , т. е.

x = xcosα + ysinα , y = −xsinα + ycosα .			(1.17)
′	′
Формулы (1.17) показывают преобразование прямоугольных коор-
динат при повороте	осей. Из (1.17) следует, что	x = x cosα − y sinα ,
		′	′

y= x′sinα + y′cosα .

Сучетом (1.16) и (1.17) можно записать преобразование прямоугольных координат при повороте и параллельном переносе осей:

x = xcosα + ysinα − a ,	y = −xsinα + ycosα −b .	(1.18)
′	′

1.9. Полярная система координат

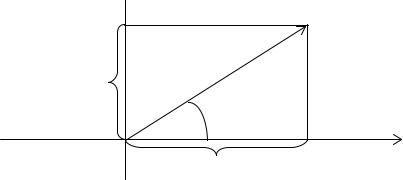
Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.

у

М

уρ

ϕ х

Ох

Определение. Полярными координатами точки М называются два числа ρ и ϕ, первое из которых (полярный радиус ρ) равно расстоянию точки М от полюса О, а второе (полярный угол ϕ) − угол, на который надо повернуть против часовой стрелки луч Ох до совмещения с лучом ОМ.

При этом предполагается, что точка М не совпадает с полюсом. Для полюса О полярный радиус ρ равен нулю, а полярный угол ϕ не определен, т. е. ему можно присвоить любое значение.

Точку плоскости М с полярными координатами ρ и ϕ обозначают символом М (ρ, ϕ).

Для того чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат (ρ, ϕ) было взаимно однозначным, обычно считают, что 0 ≤ ρ < + ∞, 0 ≤ ϕ < 2π. Однако в некоторых случаях приходится рассматривать углы, большие 2π, а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по часовой стрелке.

Установим связь между полярными и прямоугольными координатами одной и той же точки плоскости. Будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью.

Пусть точка М имеет полярные координаты ρ и ϕ и прямоугольные координаты х и у. Тогда

15

x = ρ cos ϕ, y = ρ sin ϕ .

(1.19)

Формулы (1.19) выражают прямоугольные координаты через полярные. Выражения полярных координат точки через прямоугольные следуют

из формул (1.19):
ρ = x2 + y2 , tg ϕ = xy .	(1.20)

Вторая из этих формул определяет два значения полярного угла, так как ϕ изменяется от 0 до 2π. Из этих двух значений выбирается то, при к о- тором удовлетворяются равенства (1.19), т. е. нужно, используя знаки х и у, определить квадрант, в котором находится точка М. Когда х = 0, tg ϕ не

может быть вычислен по формулам (1.20). В этом случае ϕ = π2 (если у > 0) и ϕ = 32π (если у < 0).

Для простоты нахождения полярного угла ϕ через прямоугольные координаты можно воспользоваться следующей таблицей:

Значение х	Значение у	Значение ϕ
х = 0	у > 0	ϕ =	π
			2
х = 0	у < 0	ϕ =		3π
			2
х > 0	у < 0	ϕ = arctg						y	+ 2π
								x
х > 0	у = 0	ϕ = 0
х > 0	у > 0	ϕ = arctg						y
								x
х < 0	у < 0	ϕ = arctg						y	+π
								x
х < 0	у = 0	ϕ = π
х < 0	у > 0	ϕ = arctg						y	+π
								x

1.10. Нормальное уравнение прямой

Пусть дана некоторая прямая L. Через начало координат проведем прямую n , перпендикулярную данной и пересекающую ее в точке N . Построенная прямая n называется нормалью к прямой L.

На нормали введем направление от точки O к точке N . Если точки O и N совпадают, то направление из двух возможных выберем произвольно. Прямая n с выбранным направлением является осью. Пусть α − угол, на который надо повернуть против часовой стрелки ось Ox до совмещения ее положительного направления с направлением нормали, p −

16

длина отрезка ON , тогда 0 ≤α 2π , p ≥ 0. Выведем уравнение данной прямой, считая известными угол α и длину p .

L	y	n
		N
		p	М
		α
O		ϕ	x

Введем полярную систему координат так, чтобы полюс находился в начале декартовой системы координат, а полярная ось совпадала с декартовой осью Ox . Выберем на прямой L произвольную точку M с полярными координатами (ρ,ϕ) . Если точки O и N не совпадают, то из треуголь-

ника OMN имеем: p = ρcos(α −ϕ) = ρ(cosαcosϕ +sinαsinϕ) . Это	уравнение
можно переписать в виде
ρcosαcosϕ + ρsinαsinϕ − p = 0.	(1.21)

Уравнению (1.21) удовлетворяют координаты только тех точек, которые лежат на прямой L, поэтому (1.2) является уравнением прямой в полярных координатах. Воспользовавшись формулами (1.19), в прямоугольной системе координат получим:

xcosα + ysinα − p = 0 .

(1.22)

Если точки O и N совпадают, то прямая проходит через начало координат, поэтому p = 0 . В этом случае для любой точки M прямой выпол-

няется равенство cos(ϕ −α) = 0 и соответственно ρcos(ϕ −α) = 0 , т. е. xcosα + ysinα = 0 . Таким образом, в любом случае уравнение прямой можно

представить в виде (1.22), которое называется нормальным уравнением прямой.

Рассмотрим, как привести общее уравнение прямой к нормальному виду. Пусть одна и та же прямая определяется уравнениями (1.12) и (1.22). Тогда коэффициенты этих уравнений пропорциональны, т. е.

	cosα	=		sinα		=	− p			.	(1.23)
	A				B		C				µ , тогда cosα = µA, sinα =
Пусть одно из отношений в (1.23) равно
= µB . Из основного тригонометрического											тождества следует, что
µ2 (A2 + B2 ) =1, или
µ = ±				1					.		(1.24)
				2			2
					A + B

Число µ называется нормирующим множителем. Знак µ определяется из условия µC 0 .

17

Таким образом, для приведения общего уравнения прямой к нормальному виду, надо все члены уравнения (1.12) умножить на нормирующий множитель, определяемый соотношением (1.24).

Выведем формулу для определения расстояния d от произвольной точки M0 (x0 , y0 ) плоскости до прямой L, заданной нормальным уравнени-

ем.

	L0		y		n
L					N0
				N	М0(x0, y0)
	O				x

Через точку M0 (x0 , y0 ) проведем прямую L0

параллельно прямой L.

Пусть N0

− точка пересечения прямой L0 с нормалью n , p0

− длина отрез-

ка ON0 . Если точки

N и N0 лежат по одну сторону от точки O , то нор-

мальное уравнение прямой L0

имеет вид xcosα + ysinα − p0

= 0 , так как в

этом случае для прямых L и L0 положительное направление нормали оди-

наково. Точка M0 (x0 , y0 ) принадлежит прямой L0 ,

поэтому x0 cosα + y0 sinα −

− p0 = 0 , или p0 = x0 cosα + y0 sinα . Имеем: d =

p0 − p

=

x0 cosα + y0 sinα − p

.

Если точки N и N0 лежат по разные стороны от точки O , то но р-

мальное

уравнение

прямой

L0 следующее: xcosα1 + ysinα1 − p0

= 0 , где

α1 = π −α .

Точка

M0 (x0 , y0 )

принадлежит

прямой

L0 ,

поэтому

x0 cosα + y0 sinα + p0 = 0 , откуда получаем p0 = −x0 cosα − y0 sinα . В этом случае

d = p0 + p = = − x0 cosα − y0 sinα + p = x0 cosα + y0 sinα − p .

Если точка M0 (x0 , y0 ) принадлежит прямой L, то ее координаты удовлетворяют уравнению (1.22) прямой, т. е. x0 cosα + y0 sinα − p = 0 , и d = 0 .

Таким образом, независимо от положения точки M0 (x0 , y0 ) на плоско-

сти расстояние d от нее до прямой, заданной нормальным уравнением (1.22), определяется по формуле

d =		x0 cosα + y0 sinα − p		.	(1.25)
Определение. Отклонением δ точки М от прямой					L называется

число d , если точка М и начало координат O лежат по разные стороны от прямой L, и число − d , если точки М и O лежат по одну сторону от прямой, т. е.

δ = x0 cosα + y0 sinα − p .	(1.26)
18

П р и м е р 12. Составить уравнения биссектрис углов, образованных

прямыми 4x −3y + 7 = 0 и 5x +12y −13 = 0.

Решение. Запишем нормальные уравнения этих прямых. Нормирующие множители µ1 и µ2 уравнений этих прямых найдем по формуле (1.24):

µ1 = −		1		= −	1	,	µ2 =				1				=		1		. Таким образом, нормальные урав-
					5											13
		42 + (−3)2						52 +122
нения этих прямых −							4 x +	3 y			− 7	= 0			и				5	x +	12 y −1	= 0 . Левые части этих со-
							5	5			5					13					13

отношений равны соответственно отклонениям δ1 и δ2 точки M(x, y) от этих прямых. Если точка M(x, y) находится на биссектрисе угла, в котором лежит начало координат, то эти отклонения равны, т. е. δ1 = δ2 . На другой

биссектрисе отклонения точки M от прямых равны по модулю, но противоположны по знаку, т. е. δ1 = −δ2 . Таким образом, уравнения биссектрис

	имеют вид −	4		3		7	5				12			и −	4		3		7	5				12		= 0 ,
			x +		y −		−			x +		y −1	= 0			x +		y −		+			x +		y −1
		5		5		5		13			13				5		5		5		13			13

или 11x +3y +8 = 0 и 9x −33y +52 = 0.

Из определения отклонения точки от прямой следует, что точка M(x, y) и начало координат O лежат в одном углу, образованном двумя пе-

ресекающимися прямыми, если оба отклонения δ1 и δ2 точки M(x, y) от этих прямых отрицательны. Если оба отклонения δ1 и δ2 положительны, то точки M и O расположены в вертикальных углах. Если же отклонения δ1 и δ2 противоположны по знаку, то M и O находятся в смежных углах.

1.11. Окружность

Определение. Окружностью называется множество всех точек плоскости, для которых расстояние от данной точки, называемой центром окружности, есть величина постоянная, называемая радиусом окружности.

Выведем уравнение окружности. Пусть точка M(x, y) − произвольная

точка окружности радиуса R . Введем прямоугольную систему координат, у которой начало совпадает с центром окружности O . В этом случае точка

O имеет координаты (0,0) . По определению окружности

OM

= R. Учиты-

вая, что

, получим

= R , или

OM

=

x2 + y2

x2 + y2

x2 + y2

= R2 .

(1.27)

Выражение (1.27) называется уравнением окружности с центром в точке O(0,0) и радиуса R .

Покажем, что любая точка, координаты которой удовлетворяют уравнению (1.27), принадлежит окружности с центром в точке O(0,0) и ра-

диуса R .

19

Пусть координаты точки M(x, y) удовлетворяют уравнению (1.27). Тогда OM = x2 + y2 = 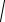x2 + (R2 − x2 ) = R2 = R , т. е. M(x, y) является точкой

окружности.

С учетом формулы преобразования прямоугольных координат точки при параллельном переносе осей получим уравнение окружности с центром в точке O(a,b) и радиуса R :

(x − a)2 + (y −b)2 = R2 .

(1.28)

П р и м е р 13. Составить уравнение окружности, проходящей через начало координат, центр которой находится на одинаковом расстоянии от

параллельных прямых 2x − y + 7 = 0 и 2x − y −7 = 0 .
Решение.	Для того чтобы составить уравнение окружности	вида
(x − a)2 + (y −b)2	= R2 , необходимо найти координаты (a,b) ее центра O	и ра-

диус R . Искомая окружность касается прямых 2x − y + 7 = 0 и 2x − y −7 = 0 ,

поэтому радиус R равен половине расстояния d между этими прямыми. Расстояние между параллельными прямыми равно расстоянию от произвольной точки одной прямой до другой прямой. На прямой, задаваемой

уравнением 2x − y + 7 = 0 , возьмем

произвольную

точку M0 (x0 , y0 ) ,

тогда

2x0 − y0 = −7 . По формуле (1.15) имеем:

d =

2x0 − y0

−7

=

−7 −7

=

14

. Таким

22 + (−1)2

5

5

образом, R =

7

. Центр окружности равноудален от заданных прямых, по-

5

этому координаты (a,b) ее центра

O должны удовлетворять равенству

2a −b + 7

=

2a −b −7

, т. е.

2a −b = 0. Известно, что окружность проходит че-

рез начало координат,

поэтому (0 − a)2 + (0 −b)2 = R2 .

Получили

систему

2a −b = 0

уравнений относительно координат центра O окружности:

2

2

49 . Ее

a

+b

=

5

решениями будут (a,b) = (± 7 , ±

14) . Итак, существует два уравнения,

удов-

5

5

7 2

14 2

49

.

летворяющих условиям задачи: x ±

+ y ±

=

5

5

5

1.12. Эллипс

Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Выберем прямоугольную систему координат таким образом, чтобы ось абсцисс проходила через фокусы F1 и F2 , а начало координат

O(0,0) совпадало с серединой отрезка F1F2 . Обозначим F1F2 = 2c , r1 + r2 = 2a ,

20

2a 2c , где r1 , r2

− фокальные радиусы (расстояния от точки до фокусов)

точки эллипса. Тогда фокусы F1 и F2

имеют координаты F1(−c,0) ,

F2 (c,0) .

y

M(x, y)

r1

r2

x

F1(−c,0)

O

F2 (c,0)

Пусть

M(x, y) − произвольная точка эллипса. Имеем:

r1 =

F1M

,

r2 =

F2M

. Из определения эллипса

= 2a ,

(1.29)

r1 + r2

или

− искомое уравнение эллипса, которое

(x + c)2 + y2

+

(x −c)2 + y2

= 2a

неудобно для

использования. Из

последнего

равенства следует, что

.Так как (x −с)2 + y2

4a2 , то можем обе части

(x + c)2 + y2

= 2a −

(x −c)2 + y2

уравнения возвести в квадрат и после эквивалентных преобразований по-

лучим: a		= a2 − xc . Следовательно,							(a2 −c2 )x2 + a2 y2 = a2 (a2 −c2 ) .
	(x −c)2 + y2
Введем новую переменную b =								. Имеем:	b2 x2 + a2 y2 = a2b2 . Из этого
					a2 −c2
равенства следует, что
			x2	+		y2	=1.		(1.30)
			a2
						b2

Уравнение (1.30) называется каноническим (простейшим) уравнением эллипса. Это уравнение является уравнением второго порядка. Таким образом, любая точка эллипса, удовлетворяющая уравнению (1.29), удовлетворяет и уравнению (1.30). Докажем, что все точки плоскости, координаты которых удовлетворяют уравнению (1.30), являются точками эллипса, т. е. их координаты удовлетворяют уравнению (1.29).

Для фокального радиуса r1	выполняется соотношение r12															= (x + c)2 + y2 .
Из уравнения (1.30) имеем:	y		= b		−	x	2		= (a		−c		−	x	2		. Поэтому
				1			2					) 1			2
		2	2							2	2
						a								a

2		xc 2	r1 = a +	xc	. Аналогично находим, что r2 = a −		xc	. Следова-
r1	= a +	, или		a			a
		a
тельно,		r1 + r2 = 2a .
	Эллипс симметричен относительно координатных осей, так как со-
держит только четные степени x и						y , и относительно начала координат.

21

Оси симметрии эллипса называются его осями, а центр симметрии − центром эллипса.

B

	b r1	r2
	с
A1		F2	А	х
F1	О	a

B1

Эллипс пересекает координатные оси в точках A(a,0) , B(0,b) , A1(−a,0) , B1(0,−b) . Эти точки называются вершинами эллипса. При a = b эллипс вы-

рождается в окружность радиусом a и центром в начале координат. Вершины эллипса ограничивают на осях отрезки длиной 2a и 2b , причем b a

(это следует из того, что b = 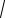a2 −c2 ).

Величины a и b называются большой и малой полуосями эллипса,

оси эллипса − соответственно большой и малой осью.

Определение. Эксцентриситетом эллипса ε называется отноше-

ние

с

, где

c

− половина расстояния между фокусами, a

− большая полу-

a

ось, т. е.

c

ε =

.

(1.31)

a

c2

a2 −b2

Учитывая,

что

c a , получим

0 ≤ ε 1. Так как

ε2 =

=

=

b 2

a2

a2

b

. Если b → a , т. е. эллипс приближается к окружно-

=

1−ε

2

=1− , то

a

a

сти, то ε →1. Если b → 0, а a к нулю не стремится, то эллипс вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру его вытянутости вдоль большой оси.

Если фокусы эллипса F1(0,c) и F2 (0,−c) расположены на оси ординат, то в этом случае b a и большой является полуось b . Уравнение эллипса также имеет вид (1.30), но a = b2 −c2 , а его эксцентриситет вычисляется

по формуле ε = bc .

П р и м е р 14. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, что расстояние между его фокусами 2c = 6 и эксцентриситет ε = 0,6 .

22

Решение. Половина расстояния между фокусами c = 3 . Фокусы эллипса расположены на оси абсцисс, поэтому большой полуосью является

a . Из (1.31) следует, что a = εc = 03,6 = 5 . Тогда b = 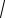a2 −c2 = 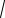52 −32 = 4 . Та-

ким образом, уравнение эллипса имеет вид x2 + y2 =1.

25 16

П р и м е р 15. Дан эллипс 9x2 +5y2 = 45 . Найти его полуоси, фокусы,

эксцентриситет.

Решение. Приведем уравнение эллипса к каноническому виду. Для

этого обе части уравнения разделим на 45, получим

x2

+

y2

=1. Таким об-

5

9

разом, его полуось a =

,

b = 3. Большой полуосью является полуось b ,

5

поэтому фокусы эллипса

расположены на оси ординат и

c = b2 − a2 =

=

= 2, следовательно,

фокусы находятся в точках (0, − 2)

и (0, 2) . Экс-

9 −5

центриситет эллипса равен отношению половины расстояния между фоку-

сами к большой полуоси, т. е. ε =								2 .
								3
П р и м е р 16. Вычислить площадь четырехугольника																															ABCD , две
вершины A и C которого лежат в фокусах эллипса 9x2 +5y2																										=1, две другие
B и D совпадают с концами его малой оси.																												x2				y2
Решение. Каноническое уравнение эллипса имеет вид																															+		=1, по-
																										1
																															1
этому a = 1 , b =	1																									9					5
				a . Следовательно, вершины четырехугольника B и D
3	5
											−	1	, 0							1	, 0		. Найдем координаты
имеют соответственно координаты												3				и				3
																2										2								2
											1		1
						2		2
вершин A и C . Так как c = b							− a			=	5	−	9		=					, то			A	0, −							, C		0,				.
																3 5									3 5									3 5

Полученный четырехугольник симметричен относительно координатных осей и относительно начала координат O , следовательно, SABCD = 4SOCD =

= 4 12 13 325 = 9 45 = 4455 .

1.13. Гипербола

Определение. Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Выберем прямоугольную систему координат таким образом, чтобы ось абсцисс проходила через фокусы F1 и F2 , а начало координат

23